Trabajo: fórmula, unidades, ejemplos, ejercicios
El trabajo en Física es la transferencia de energía que lleva a cabo una fuerza cuando se mueve el objeto sobre el cual actúa. Matemáticamente toma la forma del producto escalar entre los vectores fuerza F y desplazamiento s.
Y dado que el producto escalar entre dos vectores perpendiculares es nulo, ocurre que las fuerzas que forman 90º con el desplazamiento no hacen trabajo, según la definición, ya que:
W = F ●s = F⋅ s⋅ cos θ
Donde W denota al trabajo, por la palabra inglesa work.
La ventaja de definir el trabajo es que se trata de un escalar, es decir, no tiene dirección ni sentido, tan solo módulo y la respectiva unidad. Esto hace que sea más fácil llevar a cabo los cálculos que involucran cambios de energía causados por la acción de fuerzas.
La gravedad y el roce cinético son ejemplos de fuerzas que con frecuencia hacen trabajo sobre los objetos en movimiento. Otra fuerza común es la normal que ejerce una superficie, pero a diferencia de aquellas, esta nunca hace trabajo sobre los objetos, por ser perpendicular al desplazamiento.
Cuando un cuerpo cae libremente, la gravedad hace un trabajo positivo sobre el móvil, haciendo que este aumente su velocidad mientras cae. En cambio el roce cinético tiene un efecto completamente opuesto, ya que como siempre se opone al movimiento, lleva a cabo un trabajo negativo que no lo favorece.
Índice del artículo
- 1 Fórmulas y casos particulares
- 2 Unidades de trabajo
- 3 Ejemplos de trabajo
- 4 Ejercicio resuelto
- 5 Referencias
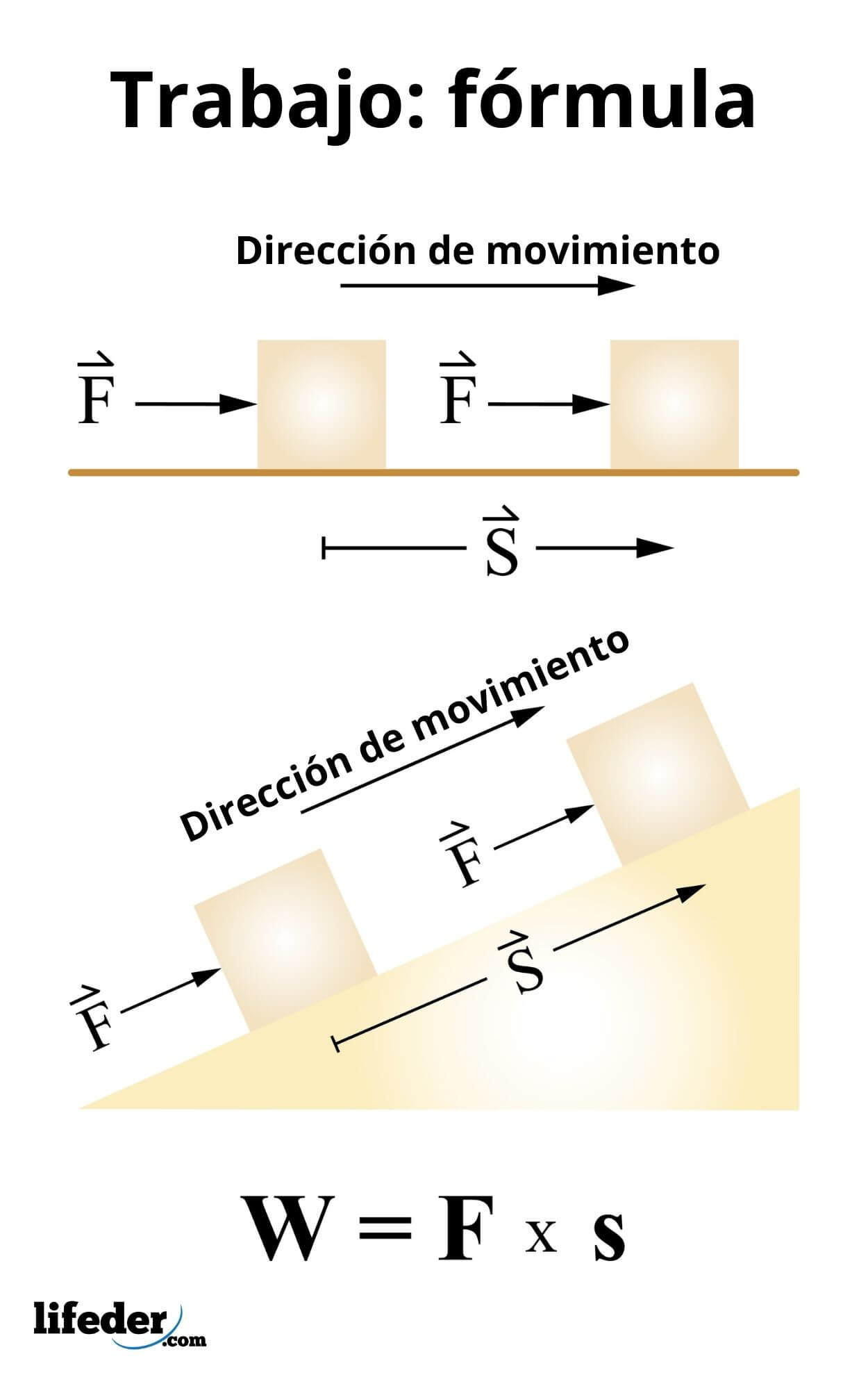
El trabajo se calcula mediante:
W = F ●s
Esta expresión es válida para fuerzas constantes y según la definición de producto escalar, equivale a:
W = F. s. cos θ
Donde θ es el ángulo que hay entre la fuerza y el desplazamiento. Se deduce pues, que únicamente aquellas fuerzas que tienen una componente en la dirección del desplazamiento pueden hacer trabajo sobre un cuerpo.
Y también se hace evidente que si no hay movimiento, tampoco hay trabajo.
En cuanto al signo, el trabajo puede ser positivo, negativo o cero. En caso de que la fuerza tenga una componente paralela al movimiento, el signo del trabajo depende del valor de cos θ.
Hay algunos casos particulares que vale la pena considerar:
- Cuando la fuerza es paralela al desplazamiento, el ángulo entre F y s es 0º, por lo tanto el trabajo realizado por la fuerza es positivo y su valor es máximo:
W = F⋅s cos 0º = F⋅s
- Si la fuerza se opone al desplazamiento entonces el ángulo entre F y s es 180º, el trabajo realizado por F es negativo y es mínimo:
W = F⋅s cos 180º = -F⋅s
- Por último se tiene el caso mencionado antes: si el ángulo formado por F y s es 90º, como cos 90º = 0, el trabajo es nulo:
W = F⋅s cos 90º = 0
A veces la fuerza aplicada no es constante; en ese caso, hay que apelar al cálculo para encontrar el trabajo realizado. En primer lugar, se determina un diferencial de trabajo dW, realizado sobre un desplazamiento infinitesimal ds:
dW = F⋅ds
Para encontrar el valor del trabajo total realizado por esta fuerza cuando el objeto va desde el punto A hasta el punto B, es necesario integrar a ambos lados, así:
La unidad para el trabajo en el Sistema Internacional es el joule, abreviado J. La unidad toma su nombre del físico inglés James Prescott Joule, pionero en el estudio de la Termodinámica.
A partir de la ecuación del trabajo, el joule se define como 1 newton por metro:
1 J = 1 N⋅m
Al trabajo le corresponde como unidad la libra-fuerza x pie, a veces llamada pie libra-fuerza. Es también una unidad para la energía, pero hay que recordar que el trabajo hecho sobre un cuerpo cambia su estado energético y que por lo tanto, el trabajo y la energía son equivalentes. No es de extrañar que tengan las mismas unidades.
La equivalencia entre el pie libra-fuerza y el joule es la siguiente:
1 pie libra-fuerza = 1,35582 J
Una unidad muy conocida para el trabajo y la energía, sobre todo para el ámbito de la refrigeración y los aires acondicionados es el BTU o British Thermal Unit.
1 BTU equivale a 1055 J y a 778.169 pie libra-fuerza.
Existen otras unidades para el trabajo que se emplean en áreas específicas de la física y la ingeniería. Entre ellas tenemos:
Ergio
Denotado como erg, es la unidad de trabajo en el sistema cegesimal y equivale a 1 dina⋅cm o 1 x 10-7 J.
Electrón-voltio
Abreviado eV, se usa comúnmente en física de partículas y se define como la energía que adquiere un electrón cuando se mueve a través de una diferencia de potencial de 1 V.
Kilovatio-hora (kWh)
Aparece con frecuencia en los recibos de las compañías de electricidad. Es el trabajo desarrollado durante 1 hora por una fuente cuya potencia es 1 kW, equivalente a 3.6 x 106 J.
Caloría
Suele relacionarse con la energía de los alimentos, aunque en realidad en este contexto se hace referencia a una kilocaloría, es decir, 1000 calorías. En realidad son varias las unidades que reciben este nombre, así que se debe especificar muy bien el contexto.
La equivalencia entre el joule y 1 caloría termoquímica es:
1 caloría = 4.1840 J
Cuando los cuerpos descienden, ya sea verticalmente o por una rampa, el peso hace trabajo positivo, favoreciendo el movimiento. En cambio, siempre que un objeto asciende, la gravedad hace trabajo negativo.
Un campo eléctrico uniforme hace trabajo sobre una carga puntual que se mueve en su interior. Dependiendo del campo y el signo de la carga, este trabajo puede ser negativo o positivo.
El rozamiento cinético entre superficies siempre hace trabajo negativo sobre el objeto que se desplaza.
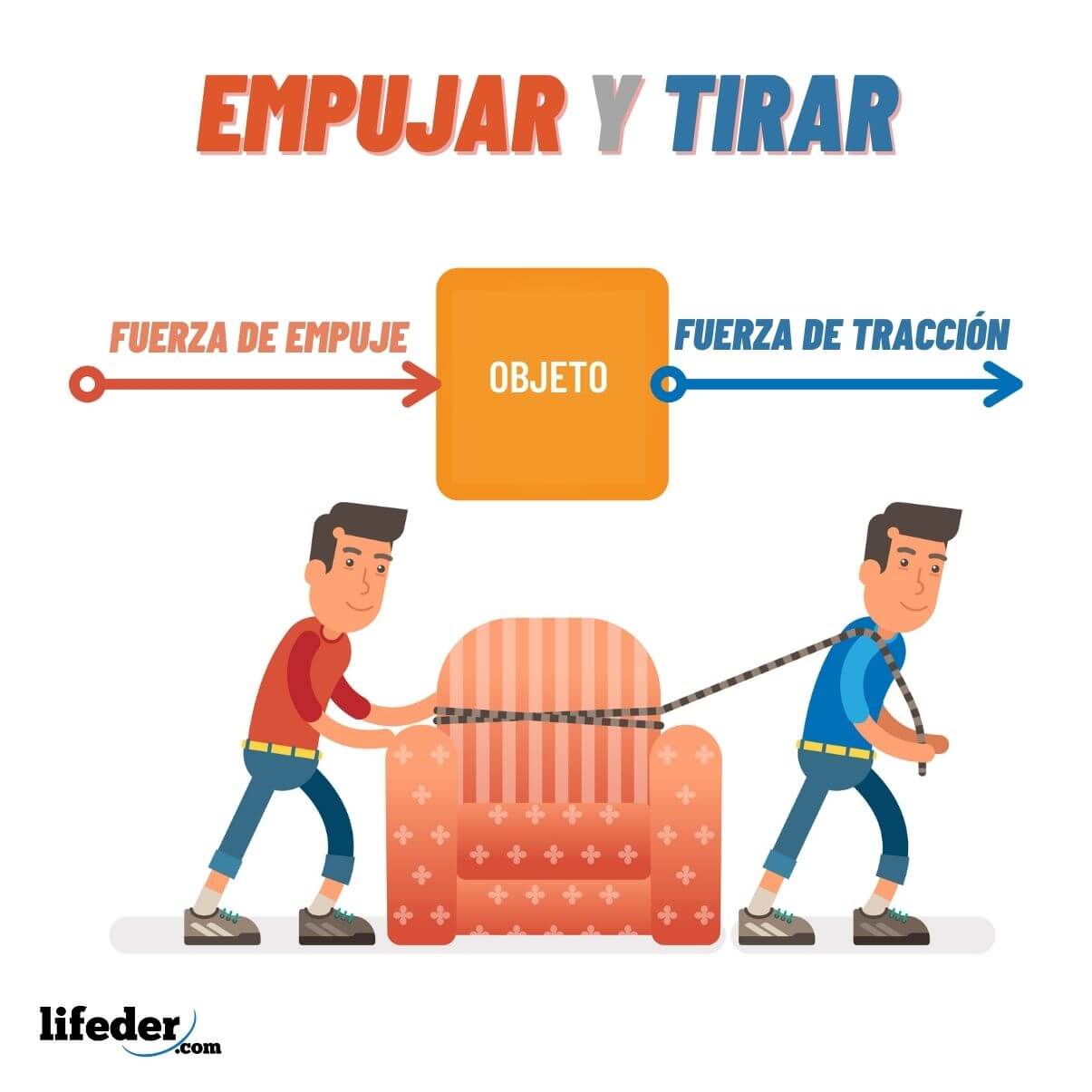
Empujar es una fuerza que aleja un objeto de algo. Tirar es una fuerza que hace que un objeto se traiga más cerca.
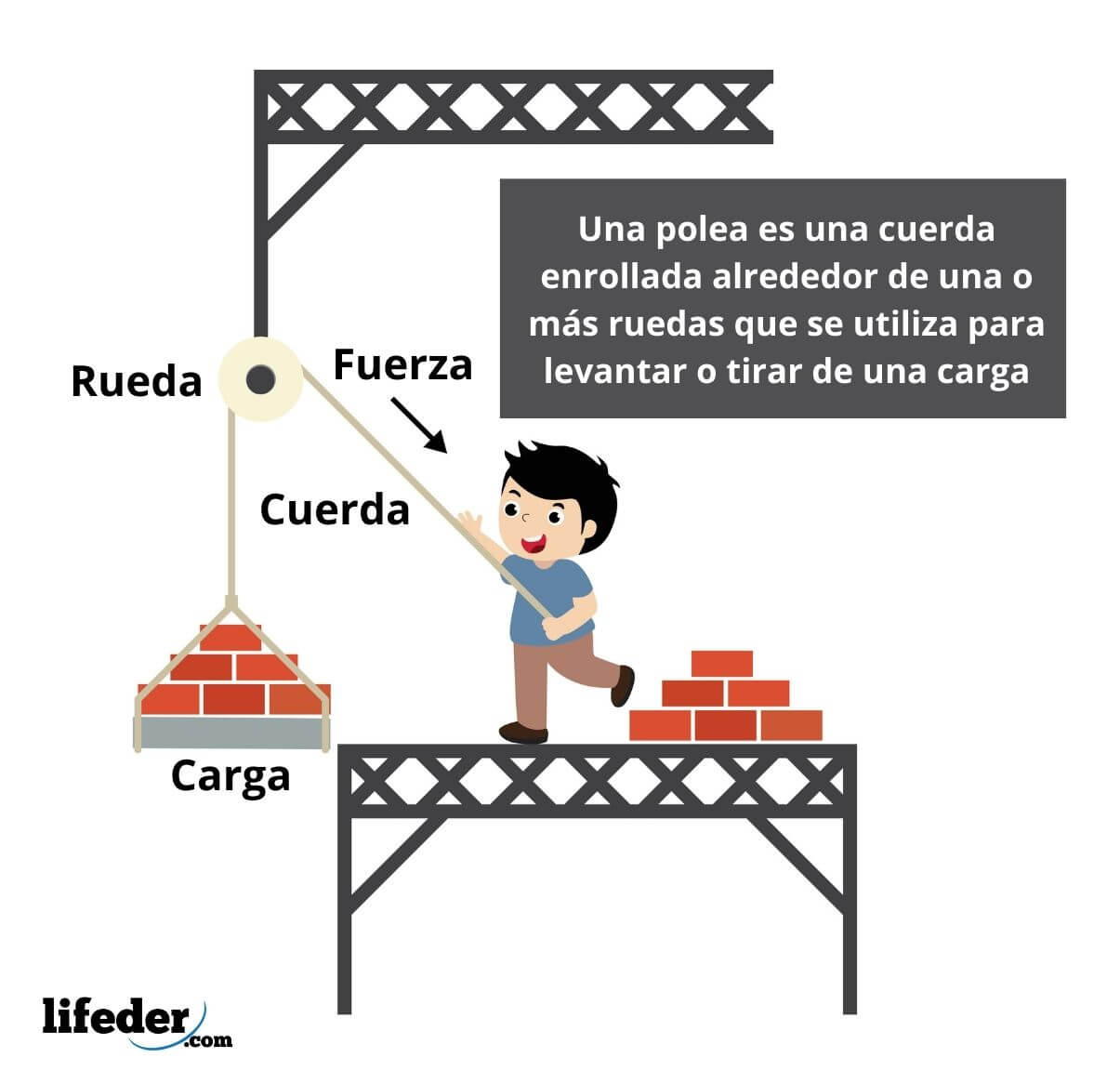
Una polea es un sistema que se utiliza para transmitir una fuerza desde uno de sus extremos. En una polea simple, para lograr levantar la carga, hay que aplicar una fuerza igual a la resistencia que ejerce el objeto.
La normal, como se indicó antes, hace un trabajo nulo cuando un objeto apoyado sobre una superficie se mueve sobre esta, aun si la superficie no es plana o si está inclinada.
Otra fuerza que hace trabajo nulo es la fuerza magnética que ejerce un campo uniforme sobre la partícula cargada que incide perpendicularmente en él. El movimiento de la partícula resulta ser un movimiento circular uniforme, con la fuerza en la dirección radial. Ya que el desplazamiento es perpendicular a la fuerza, esta no hace trabajo sobre la carga.
Una cuerda tampoco hace trabajo sobre un péndulo suspendido, ya que la tensión en ella siempre es perpendicular al desplazamiento de la masa.
La gravedad tampoco hace trabajo sobre un satélite en órbita circular, por la misma razón que los casos anteriores: es perpendicular al desplazamiento.
En un sistema masa-resorte, la fuerza F que ejerce el resorte sobre la masa tiene magnitud F = kx, donde k es la constante del resorte y x su compresión o elongación. Es una fuerza variable, por lo tanto el trabajo que realiza depende de que tanto se estire o se encoja el resorte.
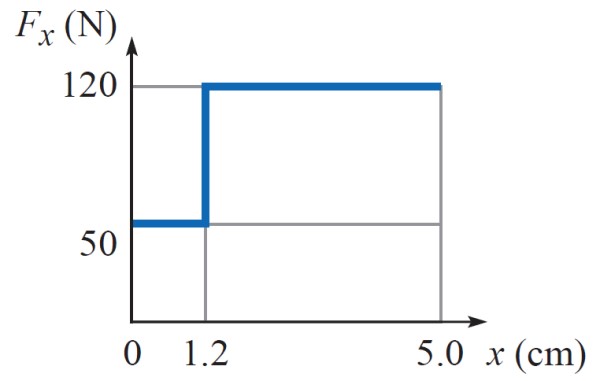
El siguiente gráfico muestra el trabajo hecho por una fuerza variable Fx que depende de la posición x. Se trata de la fuerza que ejerce un martillo sobre un clavo. La primera parte es la fuerza empleada para clavar sobre la sección más blanda de la pared y la segunda para terminar de hundir el clavo.
¿Cuánto trabajo tiene que hacer el martillo para que el clavo se hunda un total de 5 cm en la pared?
Solución
La fuerza que ejerce el martillo es variable, ya que se requiere menos intensidad (50 N) para hundir el clavo 1.2 cm en la parte blanda de la pared, mientras que en la parte más dura, son precisos 120 N para hacer que el clavo se hunda hasta 5 cm de profundidad, según muestra el gráfico.
En este caso el trabajo es la integral:
Donde A = 0 cm y B = 5 cm. Como la integral es el área bajo la gráfica Fx vs x, basta con hallar dicha área, que corresponde a dos rectángulos, el primero de altura 50 N y ancho 1.2 cm, y el segundo de altura 120 N y ancho (5 cm – 1.2 cm) = 3.8 cm.
Ambas se calculan y se suman para dar el trabajo total:
W = 50 N x 1.2 cm + 120 N x 3.8 cm = 516 N.cm = 516 N x 0.01 m = 5.16 J.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 2. Dinámica. Editado por Douglas Figueroa (USB).
- Giambattista, A. 2010. Physics. 2nd. Ed. McGraw Hill.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1. Pearson.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Ed. Cengage Learning.
- Zapata, F. Trabajo mecánico. Recuperado de: francesphysics.blogspot.com.
