Trabajo mecánico: qué es, condiciones, ejemplos, ejercicios
El trabajo mecánico se define como el cambio en el estado energético de un sistema, causado por la acción de fuerzas externas tales como la gravedad o el rozamiento. Las unidades del trabajo mecánico en el Sistema Internacional (SI) son newton x metro o joules, abreviado por J.
Matemáticamente se define como el producto escalar del vector fuerza por el vector desplazamiento. Si F es la fuerza constante y l es el desplazamiento, ambos vectores, el trabajo W se expresa como: W = F ●l

Cuando la fuerza no es constante, entonces debemos analizar el trabajo hecho cuando los desplazamientos son muy pequeños o diferenciales. En tal caso, si se considera como punto de partida al punto A y como llegada al B, el trabajo total se obtiene sumando todas las contribuciones al mismo. Esto equivale a calcular la siguiente integral:
Variación en la energía del sistema = Trabajo hecho por las fuerzas externas
ΔE = Wext
Cuando se añade energía al sistema, W>0 y cuando se le resta energía W0. Ahora bien, si ΔE = 0, puede significar que:
-El sistema se encuentra aislado y no existen fuerzas externas actuando sobre él.
-Hay fuerzas externas, pero no están realizando trabajo sobre el sistema.
Puesto que la variación en la energía equivale al trabajo hecho por las fuerzas externas, la unidad SI de la energía también es el joule. Esto incluye cualquier tipo de energía: cinética, potencial, térmica, química y más.
Índice del artículo
- 1 Condiciones para que exista trabajo mecánico
- 2 Ejemplos de trabajo mecánico
- 3 El teorema trabajo-energía cinética
- 4 Ejercicios
- 5 Referencias
Ya hemos visto que el trabajo se define como un producto escalar. Tomemos la definición de trabajo hecho por una fuerza constante y apliquemos el concepto de producto escalar entre dos vectores:
W = F ●l = F.l.cos θ
Donde F es la magnitud de la fuerza, l es la magnitud del desplazamiento y θ es el ángulo que existe entre la fuerza y el desplazamiento. En la figura 2 hay un ejemplo de fuerza externa inclinada actuando sobre un bloque (el sistema), la cual produce un desplazamiento horizontal.
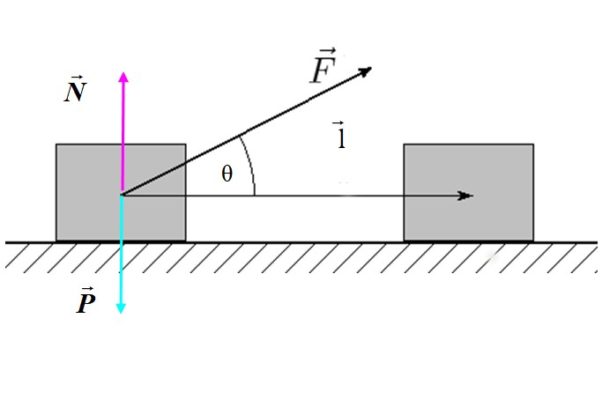
Reescribiendo el trabajo de la siguiente forma:
W = (F. cos θ). l
Podemos afirmar que solo la componente de la fuerza paralela al desplazamiento: F. cos θ es capaz de realizar trabajo. Si θ =90º entonces cos θ= 0 y el trabajo sería nulo.
Por lo tanto se concluye que las fuerzas perpendiculares al desplazamiento no hacen trabajo mecánico.
En el caso de la figura 2, ni la fuerza normal N ni el pesoP hacen trabajo, pues ambas son perpendiculares al desplazamiento l.
Como se explicó anteriormente, W puede ser positivo o negativo. Cuando cos θ > 0, el trabajo realizado por la fuerza es positivo, ya que esta tiene la misma dirección del movimiento.
Si cos θ = 1, la fuerza y el desplazamiento son paralelos y el trabajo es máximo.
En caso de que cos θ 1, la fuerza no está a favor del movimiento y el trabajo es negativo.
Cuando cos θ = -1, la fuerza es completamente opuesta al desplazamiento, como por ejemplo el roce cinético, cuyo efecto es frenar al objeto sobre el cual actúa. Entonces el trabajo es mínimo.
Esto concuerda con lo dicho al comienzo: si el trabajo es positivo, se le está añadiendo energía al sistema, y si es negativo, se está restando.
El trabajo neto Wneto se define como la sumatoria de los trabajos hecho por todas las fuerzas actuando sobre el sistema:
Wneto = ∑Wi
Entonces podemos concluir que para garantizar la existencia del trabajo mecánico neto es necesario que:
-Actúen fuerzas externas sobre el objeto.
-Dichas fuerzas no sean todas perpendiculares al desplazamiento (cos θ ≠ 0).
-Los trabajos hechos por cada fuerza no se cancelen entre sí.
-Exista un desplazamiento.
-Siempre que se requiera poner un objeto en movimiento partiendo del reposo, es necesario hacer trabajo mecánico. Por ejemplo empujar un refrigerador o un pesado baúl sobre una superficie horizontal.
-Otro ejemplo de situación en la que es necesario hacer trabajo mecánico es cambiar la rapidez de un balón en movimiento.
-Se precisa hacer trabajo para elevar un objeto a cierta altura sobre el piso.
Ahora bien, existen situaciones igualmente comunes en las que no se hace trabajo, aunque las apariencias indiquen lo contrario. Hemos dicho que para elevar un objeto a cierta altura hay que hacer trabajo, así que cargamos el objeto, lo elevamos por encima de nuestra cabeza y lo mantenemos ahí. ¿Estamos haciendo trabajo?
Aparentemente sí, porque si el objeto es pesado los brazos se cansarán al poco tiempo, sin embargo por más fuerza que se haga, no se está haciendo trabajo desde el punto de vista de la Física. ¿Por qué no? Pues porque el objeto no se está desplazando.
Otro caso en el cual, a pesar de haber una fuerza externa, esta no realiza trabajo mecánico es cuando la partícula tiene un movimiento circular uniforme.
Por ejemplo un niño que hace girar una piedra atada a un cordel. La tensión del cordel es la fuerza centrípeta que permite la rotación de la piedra. Pero en todo momento esta fuerza es perpendicular al desplazamiento. Luego no realiza trabajo mecánico, pese a que favorece al movimiento.
La energía cinética del sistema es la que este posee en virtud de su movimiento. Si m es la masa y v es la rapidez del movimiento, la energía cinética se denota por K y viene dada por:
K= ½ mv2
Por definición, la energía cinética de un objeto no puede ser negativa, ya que tanto la masa como el cuadrado de la velocidad siempre son cantidades positivas. La energía cinética puede ser 0, cuando el objeto se encuentra en reposo.
Para cambiar la energía cinética de un sistema, es preciso variar su rapidez –consideraremos que la masa permanece constante, aunque no siempre es así-. Para ello se requiere hacer trabajo neto sobre el sistema, por lo tanto:
Wneto = ΔK
Este es el teorema trabajo – energía cinética. Afirma que:
El trabajo neto equivale al cambio en la energía cinética del sistema
Nótese que aunque K siempre es positiva, ΔK puede ser positiva o negativa, ya que:
ΔK = Kfinal – K inicial
Si Kfinal >K inicial el sistema ha ganado energía y ΔK>0. Por el contrario, si Kfinal K inicial, el sistema ha cedido energía.
Cuando se estira (o se comprime) un resorte, es preciso hacer un trabajo. Este trabajo se almacena en el resorte, permitiendo que este a su vez haga trabajo sobre, digamos, un bloque que esté adosado a uno de sus extremos.
La ley de Hooke afirma que la fuerza ejercida por un resorte es una fuerza de restitución –es contraria al desplazamiento- y además proporcional a dicho desplazamiento. La constante de proporcionalidad depende de cómo es el resorte: suave y fácilmente deformable o rígido.
Esta fuerza viene dada por:
Fr = -kx
En la expresión, Fr es la fuerza, k es la constante del resorte y x es el desplazamiento. El signo negativo indica que la fuerza ejercida por el resorte se opone al desplazamiento.
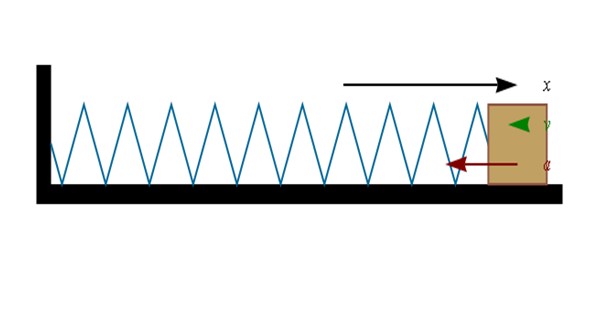
Si el resorte está comprimido (hacia la izquierda en la figura), el bloque en su extremo se desplazará hacia la derecha. Y cuando el resorte está estirado (hacia la derecha) el bloque querrá moverse hacia la izquierda.
Para comprimir o estirar el resorte, algún agente externo debe hacer el trabajo, y como se trata de una fuerza variable, para calcular dicho trabajo, hay que usar la definición que se dio al comienzo:
Es muy importante notar que este es el trabajo hecho por el agente externo (la mano de una persona, por ejemplo) para comprimir o estirar el resorte. Por eso no aparece el signo negativo. Y como las posiciones están elevadas al cuadrado, no importa si son compresiones o elongaciones.
El trabajo que hará el resorte a su vez sobre el bloque es:
Wresorte = -Wext
El bloque de la figura 4 tiene masa M = 2 kg y resbala por el plano inclinado sin fricción, con α = 36.9 º. Suponiendo que se deja resbalar desde el reposo desde lo alto del plano, cuya altura es h = 3 m, encuentre la velocidad con la que el bloque llega a la base del plano, mediante el teorema trabajo-energía cinética.
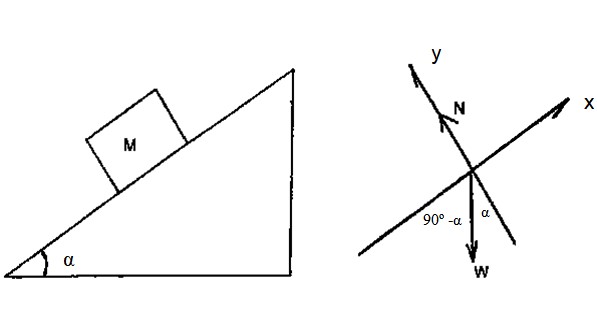
Solución
El diagrama de cuerpo libre muestra que la única fuerza capaz de hacer trabajo sobre el bloque es el peso. Más preciso: la componente del peso a lo largo del eje x.
La distancia recorrida por el bloque sobre el plano se calcula mediante trigonometría:
d = 3 / (cos 36.9º) m = 3.75 m
Wpeso = (Mg). d. cos (90-α) = 2 x 9.8 x 3.75 x cos 53.1 º J = 44.1 J
Por teorema trabajo-energía cinética:
Wneto = ΔK
Wneto = Wpeso
ΔK = ½ Mvf2– ½ Mvo2
Puesto que se suelta del reposo, vo = 0, por lo tanto:
Wneto = ½ Mvf2
Un resorte horizontal, cuya constante es k = 750 N/m se encuentra fijo por un extremo a una pared. Una persona comprime el otro extremo una distancia de 5 cm. Calcular: a) La fuerza ejercida por la persona, b) El trabajo que hizo para comprimir el resorte.
Solución
a) La magnitud de la fuerza aplicada por la persona es:
F = kx = 750 N/ m . 5 x 10 -2 m = 37.5 N.
b) Si el extremo del resorte se encuentra originalmente en x1 = 0, para llevarlo desde allí hasta la posición final x2 = 5 cm, es necesario hacer el siguiente trabajo, de acuerdo al resultado obtenido en la sección precedente:
Wext = ½ k (x22 – x12) = 0.5 x 750 x (0.052 -02) J = 0.9375 J.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 2. Dinámica. Editado por Douglas Figueroa (USB).
- Iparraguirre, L. 2009. Mecánica Básica. Colección Las Ciencias Naturales y la Matemática. Distribución gratuita online.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Physics Libretexts. Work-energy theorem. Recobrado de: phys.libretexts.org
- Work and Energy. Recobrado de: physics.bu.edu
- Work, energy and power. Recobrado de: ncert.nic.in
