x al cuadrado: qué es, ejemplos, ejercicios
La operación algebraica de “x al cuadrado” se lleva a cabo multiplicando la cantidad “x” consigo misma dos veces. Forma parte de las operaciones de potenciación, y en símbolos matemáticos, se expresa de esta forma:
x∙x = x2
Este es un caso particular de la potenciación, en la cual “x” representa la base y el “2” es el exponente. Si en una operación aparece el término x2, se lee precisamente como “x al cuadrado” o “x elevado al cuadrado”.
Naturalmente, otros exponentes son posibles, por ejemplo, si el exponente es 3, entonces la potencia se escribe como:
x∙x ∙x = x3
Y se lee como “x a la tres”, “x elevado al cubo” o simplemente “x al cubo”.
En general, el exponente al que está elevada la base puede ser cualquier número, llamado “n” y en tal caso, la potencia correspondiente se escribe:
xn = x∙x∙x∙ … ∙x
Aquí los puntos suspensivos señalan que se debe multiplicar a “x” por sí misma “n” veces, es decir, tantas veces como lo indique el exponente.
Algunos ejemplos sencillos de “x al cuadrado”, con números, son los siguientes:
32 = 3∙3 = 9
(−4)2 = (−4) ∙ (−4) = 16
Más adelante se describen diversas aplicaciones para las cuales se hace necesario calcular el cuadrado de una cantidad, pero antes que nada, conviene conocer las propiedades de la potenciación.
Propiedades de la potenciación
En general, el producto de cualquier cantidad consigo misma, n veces, recibe el nombre de potenciación. El cálculo de x al cuadrado es solamente un caso particular de potenciación, otros dos casos aparecen cuando se quiere elevar una cantidad al exponente 1, obteniéndose como resultado la misma cantidad:
Como estas operaciones son frecuentes, para trabajar con bases y exponentes se siguen algunas reglas sencillas de operación, llamadas leyes de los exponentes, que se enumeran seguidamente:
Leyes de los exponentes
En lo que sigue, “x” es la base y “n” y “m” son los exponentes.
1.- Producto de potencias de igual base
Al multiplicar dos (o más) potencias de igual base, se obtiene la base elevada a la suma de los exponentes:
xn∙xm = xn+m
En el caso de x elevada al cuadrado, esta regla se aplica de la siguiente manera, sustituyendo n y m por 1:
x1∙x1 = x1+1 = x2
2.- División de potencias de igual base
Al dividir potencias de igual base, se obtiene la base, elevada a la resta entre los respectivos exponentes del numerador y el denominador:
xn ÷ xm = xn–m
Como la división por 0 no está definida, debe cumplirse siempre que x≠0.
3.- Potencia de una potencia
El resultado de la potencia de una potencia es igual a la base elevada al producto de los exponentes:
(xm)n = xm∙n
Puede obtenerse de nuevo x al cuadrado, al hacer m = 1 y n = 2:
(x1)2 = x1∙2 = x2
4.- Exponente negativo
Para exponentes negativos, la operación a realizar es:
Siempre que x ≠ 0. Obsérvese que, en este caso, la potencia se convierte en una fracción con numerador igual a 1.
5.- Exponente fraccionario
Los exponentes fraccionarios se pueden escribir como la raíz enésima de la base:
A condición de que n sea diferente de 0. Este valor pasa a ser el índice de la raíz, mientras que m se convierte en el exponente de la cantidad bajo la raíz, que en este caso es x.
Productos y cocientes de distintas bases
Cuando hay que potenciar productos y cocientes de diferentes bases “x” y “y”, se siguen estas reglas:
1.- Potencia del producto
Para realizar esta potencia, se eleva cada cantidad al exponente n y se establece el producto resultante:
(x∙y)n = xn ⋅ yn
2.- Potencia del cociente
Nuevamente hay que elevar cada cantidad al exponente n por separado y establecer el cociente que resulta, siguiendo la norma de que la cantidad “y” sea diferente de 0, en el caso de “n” positivo:
(x ÷ y)n = xn ÷ yn
Cuando “n” es negativo, se debe tener precaución, pues de la propiedad 4 de la sección anterior, el numerador se convierte en denominador. En este caso, ambas cantidades tienen que ser distintas de 0, ya que la división por 0 debe ser evitada a toda costa.
Ejemplos
Ejemplo 1: Los cuadrados de los números naturales
Los cuadrados de los diez primeros números naturales son:
- 12= 1×1 = 1
- 22= 2×2 = 4
- 32= 3×3 = 9
- 42= 4×4 = 16
- 52= 5×5 = 25
- 62= 6×6 = 36
- 72= 7×7 = 49
- 82= 8×8 = 64
- 92= 9×9 = 81
- 102= 10×10 = 100
Ejemplo 2: El cuadrado de los números negativos
El cuadrado de un número negativo siempre es positivo, ya que se multiplican dos cantidades de igual signo, por lo tanto:
(–x)·(–x) = x∙x = x2
Por ejemplo:
(–2)·(–2) = (–2)2 = 4
Ejemplo 3: Cuadrado de la suma y de la diferencia
Con frecuencia es preciso calcular el cuadrado de la suma de dos cantidades, o su diferencia, operaciones que se incluyen en la categoría de productos notables.
La operación se resuelve con las indicaciones dadas y la ayuda de la propiedad distributiva:
Cuadrado de la suma
Sean dos cantidades “x” y “y”, y se desea hallar el cuadrado de su suma (x + y)2:
(x + y)2 = (x + y) ∙ (x + y) = x∙x + x∙y + y∙x + y∙y = x2 + 2x∙y + y2
Esta expresión se lee así: “cuadrado del primero, más el doble producto del primero por el segundo más el cuadrado del segundo”.
Cuadrado de la diferencia
Se resuelve de manera análoga, pero tomando en cuenta el signo negativo:
(x − y)2 = (x − y) ∙ (x − y) = x∙x − x∙y + y∙x − y∙y = x2 − 2x∙y + y2
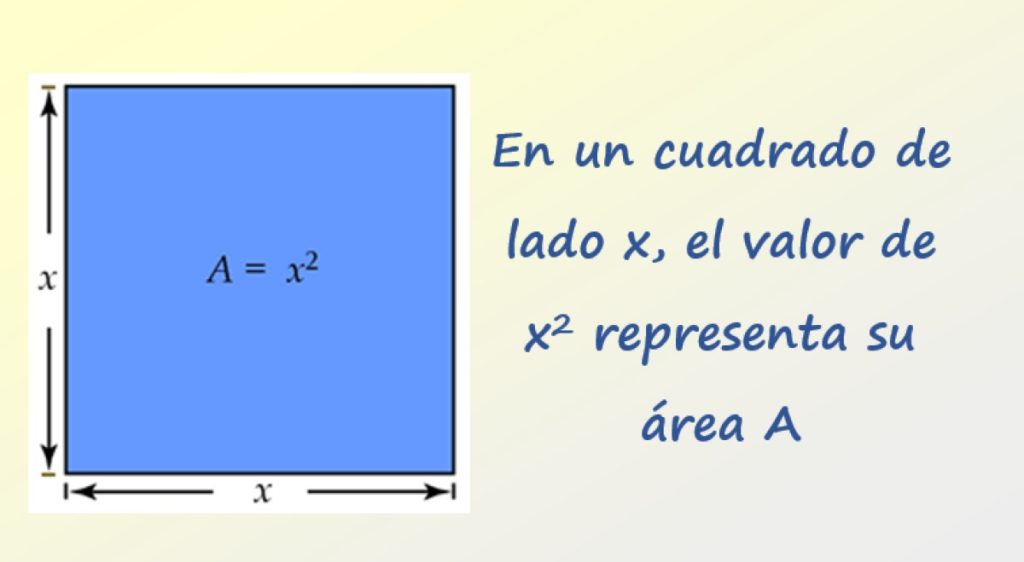
Ejemplo 4: El área de un cuadrado
El cuadrado es un polígono de 4 lados, los cuales tienen la misma medida. Sea ℓ la medida del lado, entonces el área A de la figura viene dada por:
A = ℓ2
Ejemplo 5: El teorema de Pitágoras
Este teorema se aplica a triángulos rectángulos, aquellos en los que dos de sus lados forman ángulo recto. Estos lados se conocen como “catetos” y el lado restante es la “hipotenusa”.
El teorema establece que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Llamando “a” y “b” a los catetos, y “c” a la hipotenusa, el teorema se escribe como:
c2 = a2 + b2
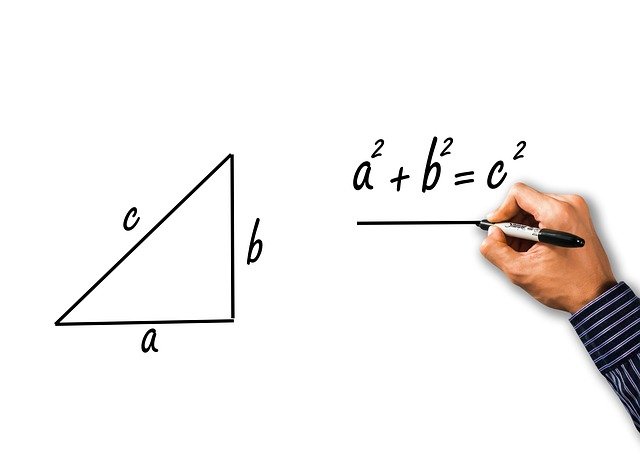
Ejercicios resueltos
Ejercicio 1
Calcular el cuadrado de la hipotenusa cuyos catetos miden 3 y 5 unidades.
Solución
Según el teorema de Pitágoras, el cuadrado de la hipotenusa es:
c2 = a2 + b2
Sustituyendo los valores:
c2 = 32 + 52= (3×3) + (5×5) = 9 + 25 = 34
Ejercicio 2
Determinar el área de un cuadrado de lado ℓ = 6 cm
Solución
A = ℓ2 = (6 cm)2 = 36 cm2
