Flujo volumétrico: concepto, cálculo y factores que lo afectan
¿Qué es el flujo volumétrico?
El flujo volumétrico permite determinar el volumen de fluido que atraviesa una sección del conducto y ofrece una medida de la velocidad con la que se desplaza el fluido por el mismo. Por tanto, su medida es especialmente interesante en ámbitos tan diversos como la industria, la medicina, la construcción y la investigación, entre otros.
Sin embargo, medir la velocidad de un fluido (ya sea un líquido, un gas o una mezcla de ambos) no es tan sencillo como lo puede ser medir la velocidad de desplazamiento de un cuerpo sólido. Por tanto, sucede que para conocer la velocidad de un fluido se hace necesario conocer su caudal.
De esta y otras muchas cuestiones relacionadas con los fluidos se ocupa la rama de la física conocida como mecánica de fluidos. El caudal se define como qué tanto fluido atraviesa una sección de un conducto, ya se trate de una tubería, un oleoducto, un río, un canal, un conducto sanguíneo, etc., tomando en consideración una unidad temporal.
Usualmente se calcula el volumen que atraviesa un área determinada en una unidad de tiempo, también llamado flujo volumétrico. También se define la masa o el flujo másico que atraviesa un área determinada en un momento específico, aunque se utiliza con menos frecuencia que el flujo volumétrico.
¿Cómo se calcula el flujo volumétrico?
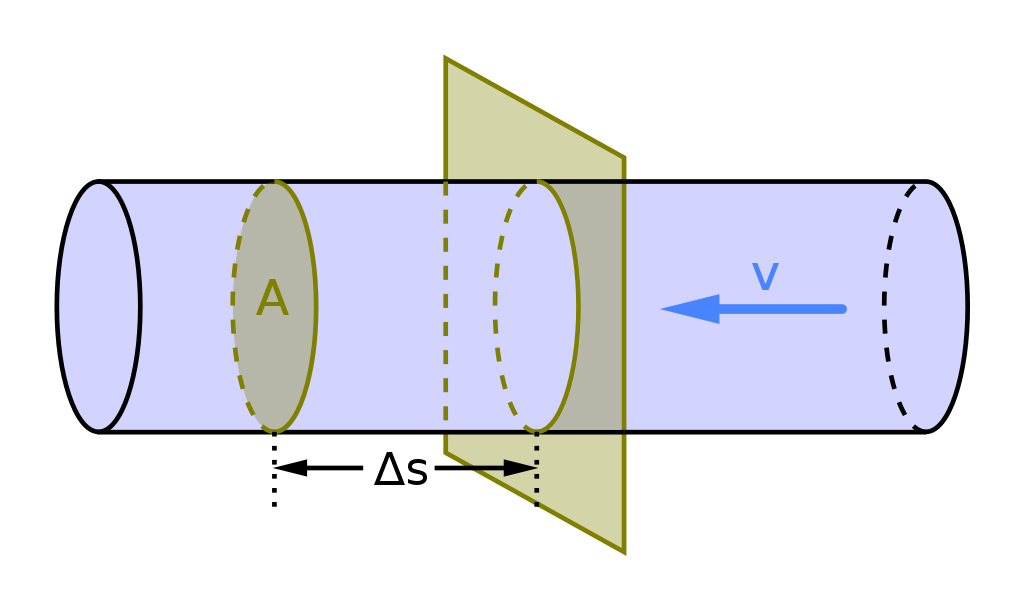
El caudal volumétrico se representa por la letra Q. Para los casos en los que el flujo se desplaza perpendicularmente a la sección del conductor, se determina con la siguiente fórmula:
Q = A = V / t
En dicha fórmula A es la sección del conductor (es la velocidad promedio que tiene el fluido), V es el volumen y t el tiempo. Dado que en el sistema internacional el área o sección del conductor se mide en m2 y la velocidad en m/s, el caudal se mide m3/s.
Para los casos en los que la velocidad del desplazamiento del fluido cree un ángulo θ con la dirección perpendicular a la sección de superficie A, la expresión para determinar el caudal es la siguiente:
Q = A cos θ
Esta es consecuente con la ecuación anterior, ya que cuando el caudal es perpendicular al área A, θ = 0 y, por consiguiente, cos θ = 1.
Las ecuaciones anteriores solo son ciertas si la velocidad del fluido es uniforme y si el área de la sección es plana. En caso contrario, el flujo volumétrico se calcula a través de la siguiente integral:
Q = ∫∫s v d S
En esta integral dS es el vector superficie, determinado por la siguiente expresión:
dS = n dS
Allí, n es el vector unitario normal a la superficie del conducto y dS un elemento diferencial de superficie.
Ecuación de continuidad
Una característica de los fluidos incompresibles es que se conserva la masa del fluido por medio de dos secciones. Por esto se cumple la ecuación de continuidad, la cual establece la siguiente relación:
ρ1 A1 V1 = ρ2 A2 V2
En esta ecuación ρ es la densidad del fluido.
Para los casos de regímenes en flujo permanente, en los que la densidad es constante y, por lo tanto, se cumple que ρ1 = ρ2, se reduce a la siguiente expresión:
A1 V1 = A2 V2
Esta equivale a afirmar que el caudal se conserva y, por tanto:
Q1 = Q2.
De la observación de lo anterior se deduce que los fluidos se aceleran cuando alcanzan una sección más estrecha de un conducto, mientras que reducen su velocidad cuando llegan a una sección más ancha de un conducto. Este hecho tiene interesantes aplicaciones prácticas, ya que permite jugar con la velocidad de desplazamiento de un fluido.
Principio de Bernoulli
El principio de Bernoulli determina que para un fluido ideal (es decir, un fluido que no tiene ni viscosidad ni rozamiento) que se desplaza en régimen de circulación por un conducto cerrado se cumple que su energía permanece constante a lo largo de todo su desplazamiento.
En última instancia, el principio de Bernoulli no es otra cosa que la formulación de la Ley de conservación de la energía para el flujo de un fluido. Así, la ecuación de Bernoulli se puede formular del siguiente modo:
h + v2 / 2g+ P/ρg = constante
En esta ecuación h es la altura y g es la aceleración de la gravedad.
En la ecuación de Bernoulli se tiene en cuenta la energía de un fluido en cualquier momento, energía que consta de tres componentes.
- Un componente de carácter cinético que incluye la energía, debida a la velocidad con la que se desplaza el fluido.
- Un componente generado por el potencial gravitatorio, como consecuencia de la altura a la que se encuentra el fluido.
- Un componente de la energía de flujo, que es la energía que posee un fluido debido a la presión.
En este caso, la ecuación de Bernoulli se expresa del siguiente modo:
h ρ g + (v2 ρ)/2 + P = constante
Lógicamente, en el caso de un fluido real la expresión de la ecuación de Bernoulli no se cumple, ya que en el desplazamiento del fluido se producen pérdidas por rozamiento y es necesario recurrir una ecuación más compleja.
¿Qué afecta al flujo volumétrico?
El flujo volumétrico se verá afectado si hay una obstrucción en el conducto.
Además, el caudal volumétrico también puede cambiar por efecto de las variaciones de temperatura y de la presión en el fluido real que se desplaza por un conducto, especialmente si este es un gas, ya que el volumen que ocupa un gas varía en función de la temperatura y la presión a las que se encuentra.
Método sencillo de medir el flujo volumétrico
Un método realmente sencillo para medir el flujo volumétrico consiste en dejar que un fluido fluya dentro de un tanque de medición durante un período de tiempo determinado.
Este método generalmente no es muy práctico, pero lo cierto es que es extremadamente sencillo y muy ilustrativo para entender el significado y la importancia de conocer el caudal de un fluido.
De este modo, se deja que el fluido fluya dentro de un tanque de medición durante un período de tiempo, se mide el volumen acumulado y se divide el resultado obtenido entre el tiempo transcurrido.
Referencias
- Caudal (Fluido) (n.d.). En Wikipedia. Recuperado de es.wikipedia.org.
- Volumetric flow rate (n.d.). En Wikipedia. Recuperado de en.wikipedia.org.
- Engineers Edge, LLC. “Fluid Volumetric Flow Rate Equation”. Engineers Edge
- Mott, Robert (1996). «1». Mecánica de fluidos aplicada (4ª edición). México: Pearson Educación.
- Batchelor, G.K. (1967). An Introduction to Fluid Dynamics. Cambridge University Press.
- Landau, L.D.; Lifshitz, E.M. (1987). Fluid Mechanics. Course of Theoretical Physics (2nd ed.). Pergamon Press.
