Curva de calibración: para qué sirve, cómo hacerla, ejemplos
La curva de calibración es una gráfica que relaciona dos variables, la cual se usa para comprobar que un equipo de medición está trabajando adecuadamente. Sin importar de qué equipo se trate, el tiempo, el uso y el desgaste natural inciden en la calidad de la medición.
Por eso es importante constatar periódicamente su buen funcionamiento. Esto se lleva a cabo comparando las medidas provistas por el equipo contra las de un dispositivo estándar usado como referencia. Este equipo de referencia es el más exacto.

Por ejemplo, en la figura 1 tenemos en verde la señal de salida de un dispositivo ideal, comparado con la magnitud medida, ambas son proporcionales.
En la misma gráfica están las curvas de dos instrumentos diferentes que no están calibrados y que tienen comportamientos ligeramente diferentes entre sí y con del estándar.
Índice del artículo
- 1 ¿Cómo funciona?
- 2 ¿Cómo hacer una curva de calibración?
- 3 Ejemplos de curva de calibración
- 4 Ejercicio resuelto
- 5 Referencias
Por ejemplo, supongamos que queremos calibrar un dinamómetro, que es un dispositivo utilizado para medir fuerzas como el peso de los objetos y las que aparecen cuando un objeto se acelera.
Para conseguir que un resorte se estire, es necesario aplicarle una fuerza, la cual es proporcional al estiramiento, de acuerdo a la ley de Hooke.
Un dinamómetro sencillo consta de un resorte dentro de un tubo provisto de un puntero y una escala para indicar el estiramiento. En uno de los extremos hay una anilla para sujetar el dinamómetro y en el otro un gancho para colgar pesas.
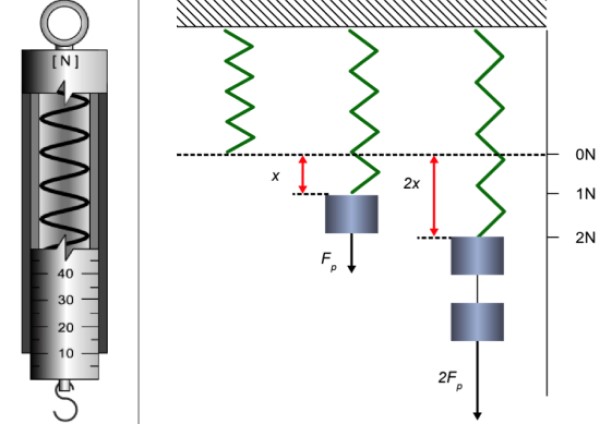
Una forma de calibrar el dinamómetro es colgando distintas pesas, cuya masa se determinó previamente con una balanza (el instrumento de referencia), y midiendo el estiramiento o elongación del resorte, que se supone liviano.
La ley de Hooke aplicada al sistema resorte-masa en equilibrio estático resulta en la siguiente ecuación, que relaciona el largo del resorte con la masa que cuelga:
L = (g/k) m + Lo
Donde:
-L: longitud total del resorte
-g: aceleración de la gravedad
-k: constante del resorte
-m: masa
-Lo: longitud natural del resorte.
Una vez que se tengan varios pares de puntos longitud-masa, se procede a graficarlos para construir la curva de calibración. Como la relación entre la longitud L y la masa m es lineal, la curva es una línea recta, donde:
Pendiente = g/k
Estos son los pasos para hacer una curva de calibración a un instrumento de medida.
Elegir el estándar de comparación a utilizar, de acuerdo al dispositivo que se quiere calibrar.
Seleccionar el rango adecuado de valores y determinar el número óptimo de medidas a realizar. Si fuésemos a calibrar un dinamómetro, tendríamos que evaluar antes el límite del peso que se le puede colgar sin que se deforme permanentemente. Si esto llegara a suceder el instrumento quedaría inservible.
Tomar pares de lecturas: una es la lectura hecha con el patrón estándar, la otra es la medida realizada con el sensor que se está calibrando.
Hacer una gráfica de los pares de lecturas obtenidos en el paso anterior. Se puede hacer a mano, sobre un papel milimetrado o mediante alguna hoja de cálculo.
La última opción es preferible, ya que el trazado a mano puede dar lugar a ligeras inexactitudes, mientras que con la hoja de cálculo se puede llevar a cabo un mejor ajuste.
Las curvas de calibración también se utilizan para convertir una magnitud en otra que sea de fácil lectura, a través de alguna propiedad o ley que las relacione.
Una alternativa al uso del mercurio es la resistencia eléctrica. La resistencia es una buena propiedad termométrica, ya que varía con la temperatura y además es fácil de medir con un ohmetro o con un amperímetro.
Pues bien, en este caso, un estándar adecuado para construir la curva de calibración sería un buen termómetro de laboratorio.
Se pueden medir parejas temperatura – resistencia y llevarlas a un gráfico, que más tarde servirá para determinar cualquier valor de temperatura conociendo la resistencia, siempre y cuando el valor de esta se encuentre dentro del rango de medidas que se haya tomado.
En la siguiente curva de calibración se tiene en el eje x la temperatura con el termómetro patrón y en el eje vertical la temperatura con un termómetro de resistencia de platino, llamado termómetro A.
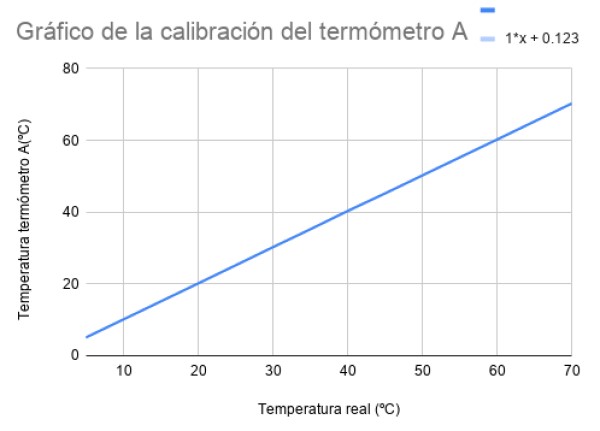
La hoja de cálculo halla la recta que se ajusta mejor a las medidas, cuya ecuación aparece en la parte de arriba a la derecha. El termómetro de platino tiene un corrimiento de 0.123 ºC respecto al patrón.
Es un método empleado en Química analítica y consiste en una curva de referencia, donde la magnitud medida es la concentración de un analito en el eje horizontal, mientras que la respuesta instrumental aparece en el eje vertical, tal como se muestra en el siguiente ejemplo.

La curva se emplea para encontrar, por interpolación, la concentración de analito presente en una muestra desconocida, a través de dicha respuesta instrumental.
La respuesta instrumental puede ser una corriente eléctrica o un voltaje. Ambas magnitudes son fáciles de medir en el laboratorio. Luego la curva se usa para averiguar la concentración del analito desconocido de esta manera:
Supongamos que la corriente sea de 1500 mA en la curva de calibración. Nos ubicamos sobre este punto en el eje vertical y dibujamos una línea horizontal hasta la curva. De este punto proyectamos una línea verticalmente hacia el eje x, donde se lee la respectiva concentración del analito.
Construir la curva de calibración de un resorte de constante elástica k y a partir de la gráfica, determinar el valor de dicha constante, todo ello a partir de los siguientes datos experimentales de parejas longitud – masa:

Cada pareja de valores se interpreta del siguiente modo:
Cuando se cuelga una masa de 1 kg, el resorte se estira hasta alcanzar 0.32 m. Si se cuelga una masa de 2 kg, el resorte llega a medir 0.40 m y así sucesivamente.
Mediante una hoja de cálculo se elabora la gráfica longitud versus masa, que resulta ser una línea recta, tal como se esperaba de la ley de Hooke, ya que la relación entre longitud L y masa m viene dada por:
L = (g/k) m + Lo
Según lo explicado en apartados anteriores. La gráfica que se obtiene es la siguiente:

Debajo del título, la hoja de cálculo muestra la ecuación de la recta que mejor ajusta los datos experimentales:
L = 0.0713 m + 0.25
El corte de la recta con el eje vertical es la longitud natural del resorte:
Lo = 0.25 m
Por su parte la pendiente es el cociente g/k:
g/k = 0.0713
Por lo tanto, tomando g = 9.8 m/s2, el valor de la constante del resorte es:
k = (9.8 /0.0713) N/m
k = 137.45 N/m
Teniendo este valor, nuestro resorte queda calibrado y el dinamómetro listo para medir fuerzas de la siguiente forma: se cuelga una masa desconocida que produce un determinado estiramiento, que se lee en el eje vertical.
De este valor se dibuja una línea horizontal hasta llegar a la curva y en dicho punto se proyecta una línea vertical hasta el eje x, donde se lee el valor de la masa. Teniendo la masa, tenemos su peso, que es la fuerza causante de la elongación.
- Serway, R., Vulle, C. 2011. Fundamentos de Física. 9na Ed. Cengage Learning.
- Tipler, P. 1987. Física Preuniversitaria. Editorial Reverté.
- Tippens, P. 2011. Física: Conceptos y Aplicaciones. 7ma Edición. McGraw Hill
- Wilson, J. 2010. Physics Laboratory Experiments. 7th. Ed. Brooks Cole.
- Wikipedia. Curva de calibración. Recuperado de: es.wikipedia.org.
