Diagrama de Moody: ecuaciones, para qué sirve, aplicaciones
El diagrama de Moody consiste en una serie de curvas dibujadas sobre papel logarítmico, que se emplean para calcular el factor de fricción presente en el flujo de un fluido turbulento a través de un conducto circular.
Con el factor de fricción f se evalúa la pérdida de energía por fricción, un valor importante para determinar el desempeño adecuado de las bombas que distribuyen fluidos tales como el agua, la gasolina, el crudo y otros.

Para conocer la energía en el flujo de un fluido es necesario conocer las ganancias y las pérdidas debido a factores como la velocidad, la altura, la presencia de dispositivos (bombas y motores), los efectos de la viscosidad del fluido y los rozamientos entre este y las paredes de la tubería.
Índice del artículo
- 1 Ecuaciones para la energía de un fluido en movimiento
- 2 ¿Para qué sirve?
- 3 ¿Cómo se hace y cómo se usa?
- 4 Aplicaciones
- 5 Referencias
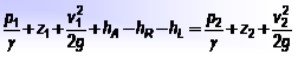
– p1 y p2 son las presiones en cada punto,
– z1 y z2 son las alturas respecto a punto de referencia,
– v1 y v2 son las respectivas velocidades del fluido,
– hA es la energía añadida mediante bombas, hR es la energía tomada por algún dispositivo tal como un motor, y hL abarca las pérdidas de energía del fluido debidas a la fricción entre este y las paredes de las tuberías, así como otras pérdidas menores.
El valor de hL se calcula mediante la ecuación de Darcy-Weisbach:
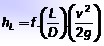
Donde L es la longitud de la tubería, D es su diámetro interior, v es la velocidad del fluido y g es el valor de la aceleración de la gravedad. Las dimensiones de hL son de longitud, y usualmente las unidades en que se representa son metros o pies.
Para calcular f se pueden usar ecuaciones empíricas obtenidas a partir de datos experimentales. Es necesario distinguir si se trata de un fluido en régimen laminar o en régimen turbulento. Para el régimen laminar f se evalúa fácilmente:
f = 64/NR
Donde NR es el número de Reynolds, cuyo valor depende del régimen en que se encuentra el fluido. El criterio es:
Flujo laminar: NR 2000 el flujo es laminar; Flujo turbulento NR > 4000; Régimen de transición: 2000 NR 4000
El número de Reynolds (adimensional) a su vez depende de la velocidad del fluido v, el diámetro interno de la tubería D y la viscosidad cinemática n del fluido, cuyo valor se obtiene mediante tablas:
NR = v.D /n
Ecuación de Colebrook
Para un flujo turbulento la ecuación más aceptada en tuberías de cobre y vidrio es la de Cyril Colebrook (1910-1997), pero tiene el inconveniente de que f no está explícito:
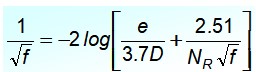
En esta ecuación el cociente e/D es la rugosidad relativa de la tubería y NR es el número de Reynolds. Al observarla cuidadosamente se advierte que no es sencillo dejar a f al lado izquierdo de la igualdad, por lo que no es conveniente para cálculos inmediatos.
El mismo Colebrook sugirió esta aproximación que sí es explícita, válida con algunas limitaciones:
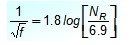
El diagrama de Moody es útil para encontrar el factor de fricción f incluido en la ecuación de Darcy, en vista de que en la ecuación de Colebrook no es sencillo expresar f directamente en términos de otros valores.
Su uso simplifica la obtención del valor de f, al contener la representación gráfica de f en función de NR para distintos valores de la rugosidad relativa sobre una escala logarítmica.
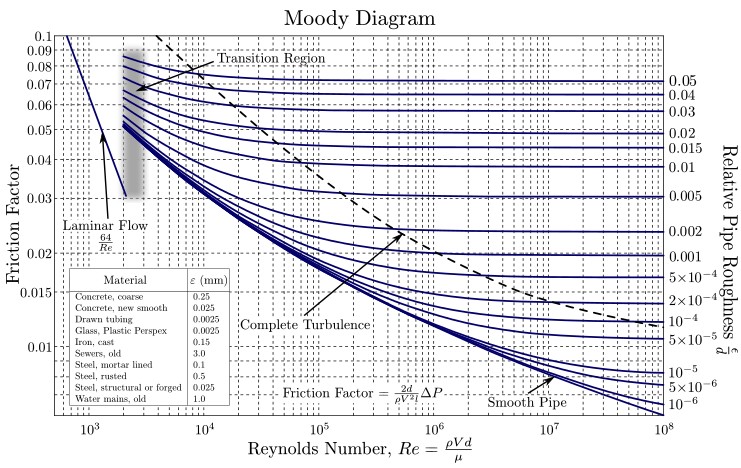
Estas curvas han sido creadas a partir de datos experimentales con diversos materiales de uso común en la fabricación de tuberías. El uso de una escala logarítmica tanto para f como para NR es necesario, puesto que abarcan un muy amplio rango de valores. De esta forma se facilita la graficación de valores de distintos órdenes de magnitud.
La primera gráfica de la ecuación de Colebrook la obtuvo el ingeniero Hunter Rouse (1906-1996) y poco después fue modificada por Lewis F. Moody (1880-1953) en la forma en que se usa actualmente.
Se utiliza tanto para tuberías circulares como para las no circulares, bastando con sustituir para estas el diámetro hidráulico.
Tal como se explicó anteriormente, el diagrama de Moody se confecciona a partir de numerosos datos experimentales, presentados en forma gráfica. Aquí están los pasos para utilizarlo:
– Calcular el número de Reynolds NR para determinar si el flujo es laminar o turbulento.
– Calcular la rugosidad relativa mediante la ecuación er = e/D, donde e es la rugosidad absoluta del material y D es el diámetro interno de la tubería. Estos valores se obtienen mediante tablas.
– Ahora que se dispone de ery NR, proyectar verticalmente hasta llegar a la curva correspondiente al er obtenido.
– Proyectar horizontalmente y hacia la izquierda para leer el valor de f.
Un ejemplo ayudará visualizar fácilmente cómo se usa el diagrama.
Determinar el factor de fricción para agua a 160º F fluyendo a razón de 22 pies/s en un ducto hecho de hierro forjado no recubierto y diámetro interno de 1 pulgada.
Solución
Datos necesarios (se encuentran en las tablas):
Viscosidad cinemática del agua a 160 ºF: 4.38 x 10-6 pie2/s
Rugosidad absoluta del hierro forjado no recubierto: 1.5 x 10 -4 pies
Primer paso
Se calcula el número de Reynolds, no sin antes pasar el diámetro interno de 1 pulgada a pies:
1 pulgada = 0.0833 pies
NR = (22 x 0.0833)/ 4.38 x 10-6= 4.18 x 10 5
De acuerdo al criterio mostrado antes se trata de un flujo turbulento, entonces el diagrama de Moody permite obtener el factor de fricción correspondiente, sin tener que utilizar la ecuación de Colebrook.
Segundo paso
Hay que encontrar la rugosidad relativa:
er = 1.5 x 10 -4 / 0.0833 = 0.0018
Tercer paso
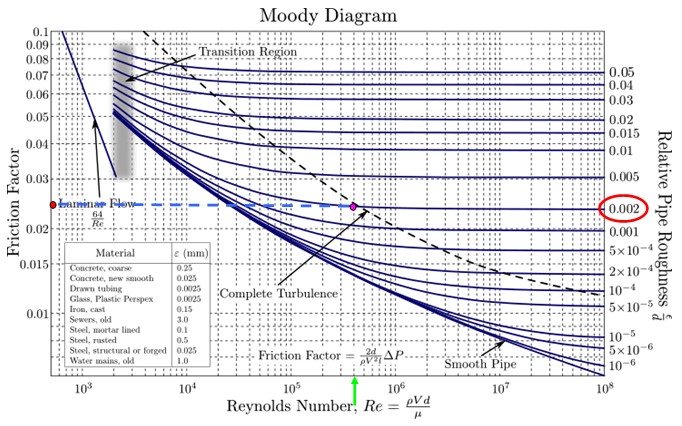
En el diagrama de Moody suministrado es necesario ubicarse a la extrema derecha y buscar la rugosidad relativa más cercana al valor obtenido. No hay ninguna que corresponda exactamente a 0.0018 pero sí hay una que se aproxima bastante, la de 0.002 (óvalo rojo de la figura).
Simultáneamente se busca el número de Reynolds correspondiente en el eje horizontal. El valor más parecido a 4.18 x 10 5 es 4 x 10 5 (flecha verde en la figura). La intersección de ambos es el punto fucsia.
Cuarto paso
Proyectar hacia la izquierda siguiendo la línea punteada azul y llegar hasta el punto naranja. Ahora estimar el valor de f, teniendo en cuenta que las divisiones no tienen el mismo tamaño al tratarse de una escala logarítmica tanto en el eje horizontal como el vertical.
El diagrama de Moody suministrado en la figura no posee divisiones horizontales finas, por lo que se estima el valor de f en 0.024 (está entre 0.02 y 0.03 pero no es la mitad sino un poco menos).
Existen calculadores en línea que utilizan la ecuación de Colebrook. Uno de ellos (ver Referencias) suministró el valor 0.023664639 para el factor de fricción.
El diagrama de Moody se puede aplicar para resolver tres tipos de problemas, siempre que se conozca el fluido y la rugosidad absoluta de la tubería:
– Cálculo de la caída de presión o de la diferencia de presiones entre dos puntos, suministradas la longitud de la tubería, la diferencia de altura entre los dos puntos a considerar, la velocidad y el diámetro interno de la tubería.
– Determinación del caudal, conocidos la longitud y el diámetro de la tubería, más la caída de presión específica.
– Evaluación del diámetro de la tubería cuando se conocen la longitud, el caudal y la caída de presión entre los puntos a considerar.
Los problemas del primer tipo se resuelven directamente mediante el uso del diagrama, mientras que los del segundo y tercer tipo requieren el uso de un paquete computacional. Por ejemplo en los del tercer tipo si no se conoce el diámetro de la tubería no se puede evaluar el número de Reynolds directamente, ni tampoco la rugosidad relativa.
Una forma para resolverlos es suponer un diámetro interno inicial y de allí ajustar sucesivamente los valores para obtener la caída de presión especificada en el problema.
Se tiene agua a 160 °F fluyendo estacionariamente a lo largo de una tubería de 1 pulgada de diámetro de hierro forjado no recubierto, a razón de 22 pies/s. Determine la diferencia de presión causada por la fricción y la potencia de bombeo necesaria para mantener el flujo en un tramo de tubería horizontal de L = 200 pies de largo.
Solución
Datos necesarios: la aceleración de gravedad es 32 pies/s2 ; el peso específico del agua a 160 ºF es γ = 61.0 lb-fuerza/pie3
Se trata de la tubería del ejemplo resuelto 1, por lo tanto ya se conoce el factor de fricción f, el cual se ha estimado en 0.0024. Este valor se lleva a la ecuación de Darcy para evaluar las pérdidas por fricción:

La potencia de bombeo necesaria es:
W = v. A. (p1 – p2)
Donde A es el área de la sección transversal del tubo: A = p. (D2/4) = p. (0.08332/4) pie2 = 0.00545 pie2
W = 22 pies /s . 2659.6 lb-fuerza / pie2. 0.00545 pie2= 318.9 lb-fuerza . pie/s
La potencia se expresa mejor en Watts, para lo cual se requiere del factor de conversión:
1 Watt = 0.737 lb-fuerza . pie/s
Por lo tanto la potencia requerida para mantener el flujo es W = 432.7 W
- Cimbala, C. 2006. Mecánica de Fluidos, Fundamentos y Aplicaciones. Mc. Graw Hill. 335- 342.
- Franzini, J. 1999. Mecánica de Fluidos con Aplicación es en Ingeniería. Mc. Graw Hill.176-177.
- LMNO Engineering. Moody Friction Factor Calculator. Recobrado de: lmnoeng.com.
- Mott, R. 2006. Mecánica de Fluidos. 4ta. Edición. Pearson Educación. 240-242.
- The Engineering Toolbox. Moody Diagram. Recobrado de: engineeringtoolbox.com
- Wikipedia. Moody Chart. Recobrado de: en.wikipedia.org
