Centro de gravedad: propiedades, cálculo, ejemplos
El centro de gravedad de un cuerpo de tamaño mensurable es el punto donde se considera que está aplicado su peso. Se trata por tanto de uno de los conceptos primordiales de la Estática.
El primer acercamiento en los problemas de Física elemental consiste en suponer que cualquier objeto se comporta como una masa puntual, es decir, carece de dimensiones y toda la masa se concentra en un solo punto. Esto es válido para una caja, un automóvil, un planeta o una partícula subatómica. A este modelo se le conoce como modelo de partícula.

Naturalmente esto se trata de una aproximación, que da muy buenos resultados para muchas aplicaciones. No es tarea fácil considerar el comportamiento individual de los miles y millones de partículas que un objeto cualquiera pude contener.
Sin embargo las dimensiones reales de las cosas deben ser tomadas en cuenta si se quieren obtener resultados que se acerquen más a la realidad. Ya que por lo general nos encontramos en las inmediaciones de la Tierra, la fuerza siempre presente sobre cualquier cuerpo es precisamente el peso.
Índice del artículo
- 1 Consideraciones para encontrar el centro de gravedad
- 2 ¿Cómo se calcula el centro de gravedad?
- 3 Propiedades
- 4 Diferencia con el centro de masa
- 5 Ejemplos de centro de gravedad
- 6 Referencias
Si se va a tomar en cuenta el tamaño del cuerpo, ¿en qué lugar de este específicamente se va a aplicar el peso? Cuando se tiene un objeto continuo de forma arbitraria, su peso es una fuerza distribuida entre cada una de sus partículas constituyentes.
Sean estas partículas m1, m2, m3… Cada una de ellas experimenta su correspondiente fuerza gravitatoria m1g, m2g, m3g…, todas ellas paralelas. Esto es así, puesto que el campo gravitatorio de la Tierra se considera constante en la inmensa mayoría de los casos, en vista de que los objetos son pequeños en comparación al tamaño del planeta y están cerca de su superficie.
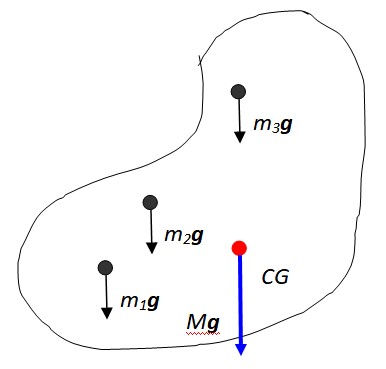
La suma vectorial de estas fuerzas da como resultado el peso del objeto, aplicado al punto llamado centro de gravedad denotado en la figura como CG, el cual coincide entonces con el centro de masas. El centro de masas a su vez es el punto donde podría considerarse concentrada toda la masa.
El peso resultante tiene magnitud Mg donde M es la masa total del objeto, y por supuesto está dirigido verticalmente hacia el centro de la Tierra. La notación de sumatoria es útil para expresar la masa total del cuerpo:
El centro de gravedad no siempre coincide con un punto material. Por ejemplo el CG de un aro está en su centro geométrico, en donde no existe masa propiamente dicha. Aún así, si se quieren analizar las fuerzas que actúan sobre un aro, hay que aplicar el peso a este punto preciso.
En los que casos en que el objeto tiene forma arbitraria, si es homogéneo aún puede calcularse su centro de masas encontrando el centroide o baricentro de la figura.
En principio si el centro de gravedad (CG) y el centro de masas (cm) coinciden al ser uniforme el campo gravitatorio, entonces puede calcularse el cm y sobre él aplicar el peso.
Consideremos dos casos: el primero es uno en el cual la distribución de masas es discreta; es decir, se puede contar cada masa que conforma el sistema y asignarle un número i, tal como se hizo en el ejemplo anterior.
Las coordenadas del centro de masa para una distribución discreta de masas son:
Naturalmente la sumatoria de todas las masas equivale a la masa total del sistema M, tal como se indicó más arriba.
Las tres ecuaciones se reducen a una forma compacta al considerar el vector rcm o vector de posición del centro de masas:
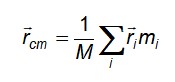
Y en caso de una distribución continua de masas, donde las partículas sean de tamaño diferencial y no se las pueda distinguir para contarlas, la sumatoria es reemplazada por una integral que se hace sobre el volumen que ocupa el objeto en cuestión:
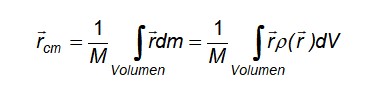
Donde r es el vector de posición de una masa diferencial dm y se ha hecho uso de la definición de densidad de masa para expresar el diferencial de masa dm contenida en un diferencial de volumen dV:
Algunas consideraciones importantes acerca del centro de masas son las siguientes:
– Si bien se requiere un sistema de referencias para establecer las posiciones, el centro de masa no depende la elección que se haga del sistema, ya que es una propiedad del objeto.
– Cuando el objeto tiene un eje o un plano de simetría, el centro de masas se encuentra sobre dicho eje o plano. Aprovechar esta circunstancia ahorra tiempo de cálculo.
– Todas las fuerzas externas que actúan sobre el objeto pueden aplicarse al centro de masas. Seguir la pista del movimiento de este punto da una idea global del movimiento del objeto y facilita el trabajo de estudiar su comportamiento.
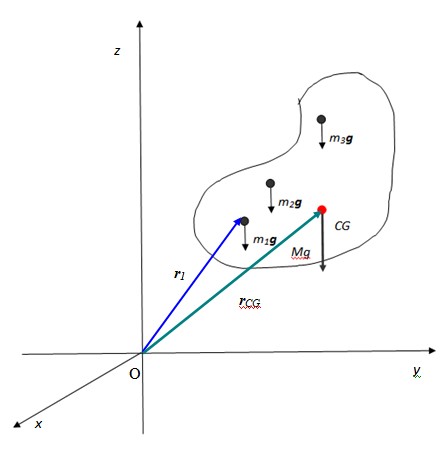
Supóngase que se desea hacer que el cuerpo de la figura anterior se encuentre en equilibrio estático, es decir, no se traslade ni tampoco rote respecto a un eje de rotación arbitrario que puede ser O.
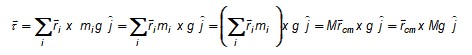
Una barra delgada de material uniforme tiene una longitud de 6 m y pesa 30 N. En su extremo izquierdo se cuelga una pesa de 50 N y otra de 20 N en su extremo derecho. Encuentre: a) La magnitud de la fuerza ascendente necesaria mantener el equilibrio de la barra, b) El centro de gravedad del conjunto.
Solución
El diagrama de fuerzas se muestra en la siguiente figura. El peso de la barra se aplica en su centro de gravedad, que coincide con su centro geométrico. La única dimensión de la barra tomada en cuenta es su longitud, ya que el enunciado informa de que es delgada.
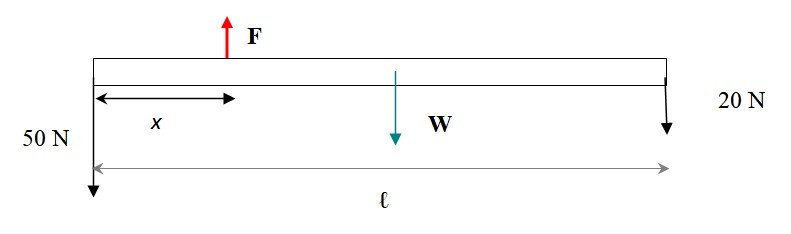
Para que el sistema de barra + pesas se mantenga en equilibrio de traslación, la sumatoria de las fuerzas debe ser nula. Las fuerzas son verticales, si consideramos hacia arriba con signo + y hacia abajo con signo – entonces:
F- 50 – 20 – 30 N = 0
F = 100 N
Esta fuerza garantiza el equilibrio de traslación. Tomando los momentos de torsión de todas las fuerzas respecto a un eje que pasa por el extremo izquierdo del sistema y aplicando la definición:
t = r x F
Los momentos de todas estas fuerzas respecto al punto seleccionado son perpendiculares al plano de la barra:
tF = xF = 100x
tW = -(l/2)mg =-3m . 30 N = -90 N.m
t1 = 0 (ya que la fuerza de 50 N pasa por el eje de giro seleccionado y no ejerce momento)
t2 = -lF2 = 6 m . 20 N = -120 N.m
Por lo tanto:
100 x -90 -120 N.m = 0
x = 2.10 m
El centro de gravedad del conjunto barra + pesas está ubicado a 2.10 metros del extremo izquierdo de la barra.
El centro de gravedad coincide con el centro de masas, tal como se ha indicado, con tal de que el campo gravitatorio terrestre sea constante para todos los puntos del objeto a considerar. El campo gravitatorio de la Tierra no es otra cosa que el conocido y familiar valor de g = 9.8 m/s2 dirigido verticalmente hacia abajo.
Aunque el valor de g experimenta variaciones con la latitud y la altitud, usualmente estas no afectan a los objetos acerca de los cuales se trata la mayor parte de las veces. Muy diferente sería si se considera un cuerpo de grandes dimensiones en las cercanías de la Tierra, por ejemplo un asteroide que se acercara mucho al planeta.
El asteroide tiene un centro de masas propio, pero su centro de gravedad ya no tendría por qué coincidir con este, puesto que g probablemente experimentaría variaciones sustanciales en magnitud, dado el tamaño del asteroide y que los pesos de cada partícula podrían no ser paralelos.
Otra diferencia fundamental es que el centro de masa se halla independientemente de si hay o no una fuerza llamada peso aplicada sobre el objeto. Es una propiedad intrínseca del objeto que nos revela cómo su masa está distribuida en relación a su geometría.
El centro de masas existe tanto si hay peso aplicado como si no. Y se ubica en la misma posición aunque el objeto se traslade a otro planeta en el cual el campo gravitatorio sea diferente.
En cambio el centro de gravedad está claramente vinculado a la aplicación del peso, tal como hemos podido apreciar a lo largo de los párrafos anteriores.
Es muy sencillo averiguar dónde está el centro de gravedad de un objeto irregular como una taza. Primero se la suspende desde un punto cualquiera y desde allí se traza una línea vertical (en la figura 5 es la línea fucsia en la imagen izquierda).
Seguidamente se la suspende desde otro punto y se traza una nueva vertical (línea turquesa en la imagen derecha). La intersección de ambas líneas es el centro de gravedad de la taza.

Analicemos la estabilidad de un camión que circula por la carretera. Cuando el centro de gravedad se encuentra por encima de la base del camión, este no volcará. La imagen de la izquierda es la posición más estable.
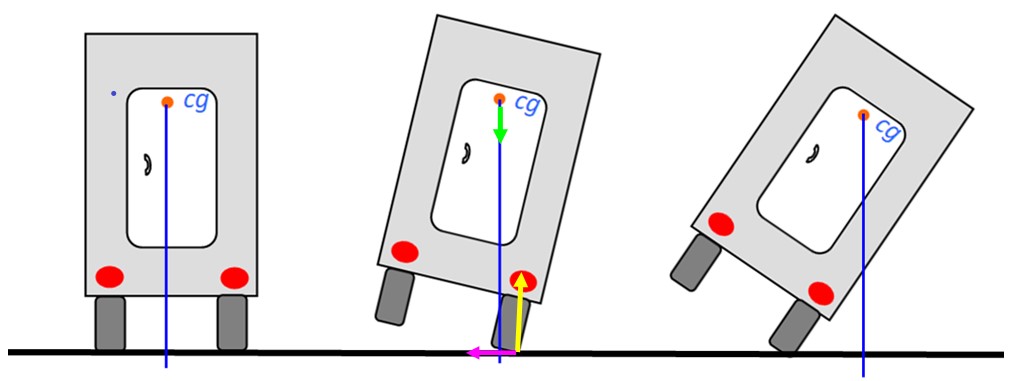
Aún cuando el camión se incline hacia la derecha podrá volver a la posición de equilibrio estable, como en el dibujo del medio, pues la vertical todavía pasa por la base. Sin embargo cuando esta línea pasa por fuera el camión se volcará.
El diagrama muestra las fuerzas en el punto de apoyo: la normal en amarillo, el peso en verde y el roce estático hacia la izquierda en fucsia. La normal y el roce están aplicadas sobre el eje de giro, por lo que no ejercen momento de torsión. Por lo tanto no van a contribuir a volcar el camión.
Queda el peso, que sí ejerce un momento de torsión, por suerte en sentido antihorario y que tiende a regresar al camión a su posición de equilibrio. Nótese que la línea de la vertical pasa por la superficie de apoyo, que es el neumático.
Cuando el camión se encuentra en la posición de la extrema derecha, el momento de torsión del peso cambia y pasa a ser en sentido horario. Al no poder ser contrarrestado por otro momento, el camión volcará.
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill. 247-253.
- Giancoli, D. 2006. Physics: Principles with Applications. 6th.. Ed Prentice Hall. 229-238.
- Resnick, R. (1999). Física. Vol. 1. 3ra Ed. en español. Compañía Editorial Continental S.A. de C.V. 331-341.
- Rex, A. 2011. Fundamentos de Física. Pearson.146-155.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1.340-346.
