Segunda ley de la termodinámica: fórmulas, ecuaciones, ejemplos
La segunda ley de la termodinámica tiene varias formas de expresión. Una de ellas afirma que ninguna máquina térmica es capaz de convertir completamente toda la energía que absorbe en trabajo utilizable (formulación de Kelvin-Planck). Otra manera de enunciarla es decir que los procesos reales ocurren en un sentido tal, que la calidad de la energía es menor porque la entropía tiende a aumentar.
Esta ley, también conocida como segundo principio de la termodinámica, se ha expresado de diferentes maneras con el pasar del tiempo, desde los comienzos del siglo XIX hasta la actualidad, si bien sus orígenes datan de la creación de las primeras máquinas de vapor en Inglaterra, a comienzos del siglo XVIII.

Pero aunque se la exprese de muchas formas, en todas subyace la idea de que la materia tiende a desordenarse y que ningún proceso tiene eficiencia del 100%, ya que las pérdidas siempre existirán.
Todos los sistemas termodinámicos se apegan a este principio, comenzando por el universo mismo hasta la taza de café mañanero que espera tranquilamente sobre la mesa intercambiando calor con el entorno.
El café se enfría conforme pasa el tiempo, hasta quedar en equilibrio térmico con el ambiente, así que sería muy sorprendente que un día pasara lo contrario y el ambiente se enfriara mientras que el café se calentara por sí mismo. Es improbable que suceda, algunos dirán que imposible, pero basta con imaginarlo para tener una idea del sentido en que las cosas pasan espontáneamente.
En otro ejemplo, si hacemos deslizar un libro sobre la superficie de una mesa, este eventualmente se detendrá, debido a que su energía cinética se perderá en forma de calor debido al rozamiento.
La primera y la segunda ley de la termodinámica se establecieron alrededor de 1850, gracias a científicos de la talla de lord Kelvin –creador del término “termodinámica”-, William Rankine –autor del primer texto formal de termodinámica- y Rudolph Clausius.
Índice del artículo
La entropía -mencionada al comienzo-, nos ayuda a establecer el sentido en que las cosas ocurren. Volvamos al ejemplo de los cuerpos en contacto térmico.
Cuando dos objetos a diferentes temperaturas se ponen en contacto y finalmente después de un tiempo llegan al equilibrio térmico, son impulsados a ello por el hecho de que la entropía alcanza su máximo, cuando la temperatura de ambos es la misma.
Denotando a la entropía como S, el cambio en la entropía ΔS de un sistema viene dado por:
El cambio de la entropía ΔS señala el grado de desorden en un sistema, pero existe una restricción en el uso de esta ecuación: es aplicable únicamente a procesos reversibles, es decir, aquellos en los que el sistema puede retornar a su estado original sin dejar huella de lo sucedido-.
En los procesos irreversibles, la segunda ley de la termodinámica se manifiesta así:
La taza de café siempre se enfría y es un buen un ejemplo de proceso irreversible, ya que ocurre siempre en una sola dirección. Si se agrega crema al café y agita, se obtendrá una combinación muy agradable, pero por más que se agite de nuevo, no se volverá a tener el café y la crema por separado, porque revolver es irreversible.

Pese a que la mayor parte de los procesos cotidianos son irreversibles, algunos son casi reversibles. La reversibilidad es una idealización. Para que se lleve a cabo, el sistema debe cambiar muy lentamente, de tal manera que en cada punto siempre se encuentre en equilibrio. De esta forma es posible retornarlo a un estado anterior sin dejar huella en los alrededores.
Los procesos que se acercan bastante a este ideal son más eficientes, ya que entregan una mayor cantidad de trabajo con menos consumo de energía.
La fuerza de fricción es la responsable de buena parte de la irreversibilidad, porque el calor generado por ella no es el tipo de energía que se busca. En el libro deslizando por encima de la mesa, el calor por fricción es energía que no se recupera.
Aunque el libro vuelva a su posición original, la mesa habrá quedado caliente como huella del ir y venir sobre ella.
Ahora observe un bombillo incandescente: la mayor parte del trabajo hecho por la corriente que atraviesa el filamento se desperdicia en calor por efecto Joule. Apenas un pequeño porcentaje se usa para emitir luz. En ambos procesos (libro y bombillo), la entropía del sistema ha aumentado.
Un motor ideal es el aquel que se construye mediante procesos reversibles y carece de rozamientos que ocasionan desperdicios de energía, convirtiendo casi toda la energía térmica en trabajo utilizable.
Hacemos énfasis en la palabra casi, porque ni siquiera el motor ideal, que es el de Carnot, tiene eficiencia de 100%. La segunda ley de la termodinámica se ocupa de que no sea así.
El motor de Carnot es el motor más eficiente que se puede idear. Opera entre dos depósitos de temperatura en dos procesos isotérmicos – a temperatura constante- y dos procesos adiabáticos –sin transferencia de energía térmica-.
Las gráficas llamadas PV –diagramas de presión – volumen– aclaran de un vistazo la situación:
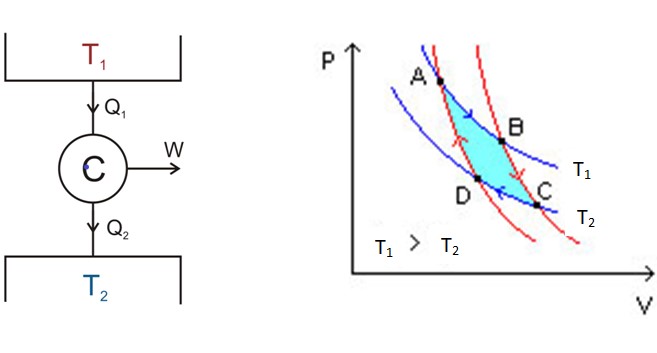
A la izquierda, en la figura 3 está el esquema del motor de Carnot C, el cual toma calor Q1 del depósito que está a temperatura T1, convierte ese calor en trabajo W y cede el desecho Q2 al depósito más frío, que está a temperatura T2.
Partiendo de A, el sistema se expande hasta llegar a B, absorbiendo calor a la temperatura fija T1. En B, el sistema comienza una expansión adiabática en la cual no gana ni se pierde calor, para llegar hasta C.
En C empieza otro proceso isotérmico: el de ceder calor al otro depósito térmico más frío que está a T2. A medida que esto sucede el sistema se comprime y se llega al punto D. Allí empieza un segundo proceso adiabático para retornar al punto de partida A. De esta manera se completa un ciclo.
La eficiencia del motor de Carnot depende de las temperaturas en kelvin de los dos depósitos térmicos:
Eficiencia máxima = (Qentrada – Qsalida) /Qentrada = 1 – (T2/T1)
El teorema de Carnot afirma que esta es la máquina térmica más eficiente que hay, pero no se apresure a comprarla. ¿Recuerda lo que dijimos acerca de la reversibilidad de los procesos? Tienen que ocurrir muy, muy lentamente, así que la potencia de salida de esta máquina es prácticamente nula.
Los seres humanos necesitan energía para mantener funcionando todos sus sistemas, por lo tanto se comportan como máquinas térmicas que reciben energía y la transforman en energía mecánica para, por ejemplo, moverse.
La eficiencia e del cuerpo humano al hacer un trabajo se puede definir como el cociente entre la potencia mecánica que puede proporcionar y la entrada total de energía, que llega con los alimentos.
Como la potencia media Pm es trabajo W realizado en un intervalo de tiempo Δt, se puede expresar como:
Pm = W/Δt
Si ΔU/Δt es la tasa a la que se agrega la energía, la eficiencia corporal queda como:
Mediante numerosas pruebas con voluntarios se ha llegado a obtener eficiencias de hasta un 17%, entregando unos 100 watts de potencia durante varias horas.
Claro que eso va a depender en gran medida de la tarea que se haga. Pedalear una bicicleta tiene una eficiencia un poco mayor, de alrededor del 19%, mientras que tareas repetitivas que incluyen palas, picos y azadones tienen una eficiencia tan baja como un 3 % aproximadamente.
La segunda ley de la termodinámica se encuentra implícita en todos los procesos que ocurren en el Universo. La entropía siempre es creciente, aunque en algunos sistemas parezca disminuir. Para que esto suceda ha debido aumentar en otra parte, de manera que en el balance total es positivo.
– En el aprendizaje hay entropía. Hay personas que aprenden las cosas bien y rápido, además de ser capaces de recordarlas luego con facilidad. Se dice que son personas con aprendizaje de baja entropía, pero seguramente son menos numerosas que las de alta entropía: aquellas a las que le cuesta más acordarse de las cosas que estudian.
– Una empresa con trabajadores desorganizados tiene más entropía que una en la cual los trabajadores lleven a cabo las tareas de forma ordenada. Está claro que esta última será más eficiente que la primera.
– Las fuerzas de fricción generan menos eficiencia en el funcionamiento de las maquinarias, porque aumentan la cantidad de energía disipada que no puede emplearse eficientemente.
– Lanzar un dado tiene una mayor entropía que lanzar una moneda al aire. Después de todo, lanzar una moneda solamente tiene 2 resultados posibles, mientras que lanzar el dado tiene 6. Cuantos más eventos sean probables, más entropía existe.
Un cilindro con pistón se llena con una mezcla de líquido y vapor de agua a 300 K y se le transfieren al agua 750 kJ de calor mediante un proceso a presión constante. Como resultado, el líquido dentro del cilindro se vaporiza. Calcular el cambio de la entropía en el proceso.
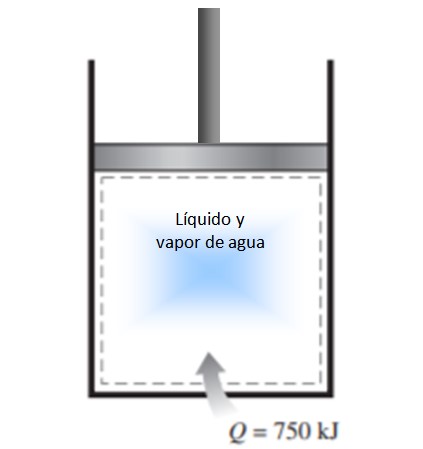
Solución
El proceso descrito en el enunciado se lleva a cabo a presión constante en un sistema cerrado, que no experimenta intercambio de masa.
Puesto que se trata de una vaporización, durante la cual la temperatura tampoco cambia (durante los cambios de fase la temperatura es constante), se puede aplicar la definición de cambio de entropía dada anteriormente y la temperatura puede salir fuera de la integral:
ΔS= 750.000 J / 300 K = 2500 J/K.
Dado que al sistema entra calor, el cambio en la entropía es positivo.
Un gas sufre un aumento de presión de 2.00 a 6.00 atmósferas (atm), manteniendo un volumen constante de 1.00 m3, para después expandirse a presión constante hasta llegar a un volumen de 3.00 m3. Finalmente regresa a su estado inicial. Calcular cuánto trabajo se lleva a cabo en 1 ciclo.
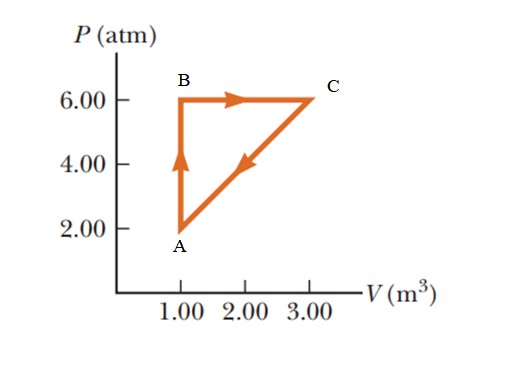
Solución
Se trata de un proceso cíclico en el cual la variación de energía interna es nula, según la primera ley de la termodinámica, por lo tanto Q = W. En un diagrama P-V (presión – volumen), el trabajo realizado durante un proceso cíclico equivale al área encerrada por la curva. Para dar los resultados en el Sistema Internacional es necesario efectuar un cambio de unidades en la presión mediante el siguiente factor de conversión:
1 atm = 101.325 kPa = 101.325 Pa.
El área encerrada por la gráfica corresponde a la de un triángulo cuya base (3 – 1 m3) = 2 m3 y cuya altura es (6 – 2 atm) = 4 atm = 405.300 Pa
WABCA = ½ (2 m3 x 405300 Pa) = 405300 J = 405.3 kJ.
Se dice que una de las máquinas más eficientes que se han construido es una turbina de vapor alimentada por carbón en el río Ohio, la cual se usa para accionar un generador eléctrico operando entre 1870 y 430 °C.
Calcular: a) La máxima eficiencia teórica, b) La potencia mecánica que entrega la máquina si absorbe 1.40 x 105 J de energía cada segundo desde el depósito caliente. Se sabe que la eficiencia real es de 42.0%.
Solución
a) La máxima eficiencia se calcula con la ecuación dada anteriormente:
Eficiencia máxima= (Qentrada – Q salida) /Qentrada = 1 – (T2/T1)
Para pasar los grados centígrados a kelvin basta con sumar 273.15 a la temperatura centígrada:
Multiplicando por 100% se tiene la máxima eficiencia porcentual, que es del 67.2%
c) Si la eficiencia real es de 42%, se cuenta con una eficiencia máxima de 0.42.
La potencia mecánica entregada es: P = 0.42 x 1.40 x10 5 J/s = 58800 W.
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.
- Cengel, Y. 2012. Termodinámica. 7ma Edición. McGraw Hill.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 4. Fluidos y Termodinámica. Editado por Douglas Figueroa (USB).
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach.
- López, C. La Primera Ley de la Termodinámica. Recobrado de: culturacientifica.com.
- Serway, R. 2011. Fundamentos de Física. 9na Cengage Learning.
- Universidad de Sevilla. Máquinas Térmicas. Recobrado de: laplace.us.es
