Variación proporcional directa e inversa: ejemplos y ejercicios

¿Qué es la variación proporcional?

La variación proporcional entre dos variables “x” e “y” tiene lugar cuando, al multiplicar una de ellas por una constante, la otra queda asimismo multiplicada o dividida por esa misma constante. Muchas situaciones del mundo real se pueden describir adecuadamente con ellas.

La proporcionalidad entre las variables puede ser directa o inversa. En la proporcionalidad directa, la relación es del tipo:

y = k∙x

O equivalentemente:

k = y/x

Donde k es una constante llamada constante de proporcionalidad o razón de proporcionalidad. Nótese que si “x” aumenta, “y” lo hace en la misma proporción, y si “x” disminuye, también lo hará “y”. Cuando se grafica la relación entre las variables se obtiene una línea recta que pasa por el origen del sistema de coordenadas (ver el ejercicio resuelto más adelante).

La variación directa también puede darse entre una variable y una potencia de la otra, por ejemplo, “y” puede ser directamente proporcional a x², x³ y así.

Por otra parte, en la proporcionalidad inversa, las variables se vinculan a través de la expresión:

x∙y= k

Esta expresión quiere decir que el producto de las variables es una constante. Al graficar la relación entre las variables resulta una hipérbola. Asimismo, si el producto de una variable con una potencia de la otra es constante, también representa un caso de proporcionalidad inversa, por ejemplo:

x²∙y= k ; x³∙y= k …

Ejemplos

Muchas leyes de la física y la química se expresan matemáticamente como proporciones. Por ejemplo, la fuerza que ejerce un resorte y la elongación del mismo, la relación entre la presión y el volumen en un gas a temperatura constante, el período de un péndulo simple y la raíz cuadrada de su longitud y muchos más. Conociendo el modelo que rige el fenómeno, se puede averiguar su comportamiento para cualquier valor de las variables.

Y no solo eso, también se aplican en innumerables situaciones como estas:

• Pasar el patrón de una prenda de vestir de una talla más pequeña a una talla más grande (o viceversa).
• En los factores de conversión, para pasar de una unidad a otra, como por ejemplo kilómetros a millas, galones a litros y más.
• Calcular los ingredientes de una receta para 6 personas conociendo el requerimiento para 4 personas.
• Determinar el monto de ciertos impuestos conforme a los ingresos obtenidos.
• En el cálculo del interés simple.
• Al dibujar planos a escala.
• Cuando hay que calcular el precio de una cantidad de productos conociendo el precio unitario.
• En la semejanza de triángulos.

A continuación, en detalle, hay dos interesantes situaciones donde se aplican las variaciones proporcionales:

Ejemplo 1

Sobre el plano a escala de una ciudad, la avenida de La Ermita mide 3.2 cm, siendo su longitud real de 400 m. En cambio, la calle de La Fuente, que realmente mide 180 m de largo tiene que dibujarse con un trazo proporcionalmente más corto. ¿Cuál es el tamaño del trazo?

El enunciado ofrece la información completa de la avenida de La Ermita: sea L la longitud real de la avenida y ℓ su longitud sobre el plano, como la variación es de proporcionalidad directa, se tiene que:

L = k∙ℓ

A partir de los datos de la avenida de La Ermita se puede conocer el valor de la constante de proporcionalidad k, pero antes es necesario dejar todas las longitudes en las mismas unidades:

3.2 cm = 0.032 m

Entonces:

400 m = k∙ 0.032 m

Por lo tanto la constante de proporcionalidad es:

k = 400 / 0.032 = 12500

Ahora se sabe que:

L = 12500 ∙ℓ

Este resultado se interpreta así: la longitud de las calles sobre este mapa son 12500 veces más pequeñas que su longitud real. Por lo tanto el trazo de la calle de La Fuente mide:

ℓ = 180 m/ 12500 = 0.0144 m = 1.44  cm

Ejemplo 2

Un analista tiene la siguiente tabla de valores para las variables “x” e “y” obtenidas experimentalmente y quiere saber si estos datos se ajustan a un modelo de variación proporcional directa o a uno de variación proporcional inversa.

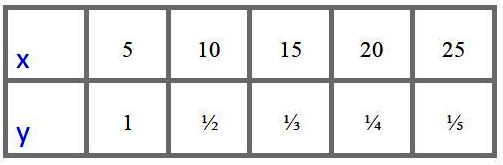
¿Qué debe hacer para saberlo?

En primer lugar se observa que cuando “x” aumenta, “y” disminuye, por lo que sospecha una proporcionalidad inversa, de todas formas, para asegurarse, el analista tiene la opción de evaluar si el cociente y/x es constante (variación proporcional directa) o si el producto x.y es constante (variación proporcional inversa).

Probando con la primera opción:

1÷5 = 0.2

½ ÷ 10 = 0.05

⅓ ÷ 15 = 0.022…

Se concluye que no es una variación proporcional directa, porque el cociente y/x da distintos valores para cada pareja de datos.

Falta comprobar si el producto x∙y es constante:

5×1 = 5

10 × ½ = 5

15 × ⅓ = 5

20 × ¼ = 5

25 × ⅕ = 5

Y como el producto x∙y = 5 se concluye que la variación es de proporcionalidad inversa.

Esta información sirve para conocer valores que no están en la tabla, por ejemplo, ¿Cuál sería el valor de “y” cuando x = 30?

A partir de x∙y = 5, se despeja “y” y se sustituye x = 30:

y = 5/x

y = 5/30 = 1/6

Ejercicio resuelto

Si un metro de tela cuesta 6.75 $, y sabiendo que el precio es directamente proporcional a la cantidad de metros a comprar, hallar:

a) La expresión algebraica que vincula las variables “precio en $” y “cantidad de metros de tela”.

b) Elaborar una tabla de valores con los precios para 3, 6, 9, 12, 15 y 18 metros de tela.

c) Graficar los valores obtenidos.

Respuesta a

Sea “y” la variable “precio en $” y “x” la variable “cantidad de metros de tela”. Como son  directamente proporcionales, se tiene que:

y = k∙x

Para x = 1 metro, y = 6.75$, por lo tanto k = 6.75 $/metro. Este es el precio unitario de la tela, el precio de cualquier otra cantidad de tela “x” se obtiene multiplicando por este valor, luego, la expresión algebraica buscada es:

y = 6.75∙x

Respuesta b

La tabla de valores con los precios en $ para 3, 6, 9, 12, 15 y 18 metros es:

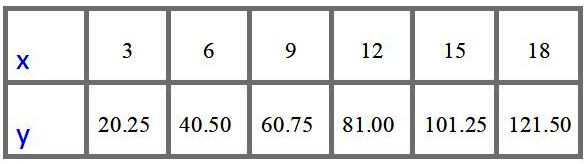
Respuesta c

Finalmente, la gráfica de los valores en la tabla anterior corrobora que se trata de una variación proporcional directa:

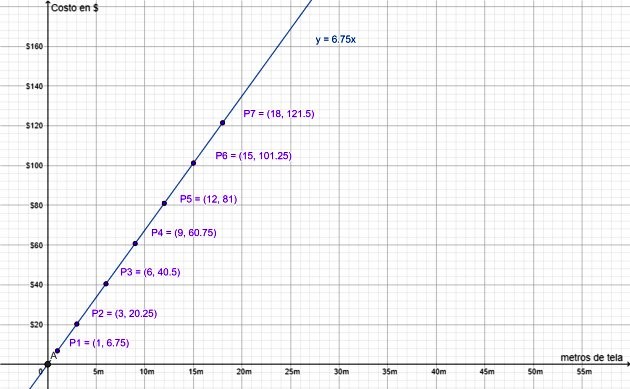
Obsérvese que el valor (0,0) está incluido, ya que la recta y = 6.75∙x pasa por el origen del sistema de coordenadas, como se explicó antes. Tiene sentido, puesto que no hacer compra alguna equivale a comprar 0 m de tela, cuyo valor es 0 $.

Referencias

1. Larson, R. 2012. Pre-cálculo. 8va. Edición. Cengage Learning.
2. Secretaría de Educación Pública de México. La variación proporcional. Recuperado de: pps.k12.or.us.
3. Stewart, J. 2007. Pre-cálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.
4. UNAM. Guías de Estudio: Matemáticas I. Recuperado de: dgire.unam.mx.
5. Zill, D. 2008. Pre-cálculo con avances de Cálculo. 4ta. Edición. McGraw Hill.