Variable continua: características, ejemplos y ejercicios
La variable continua es aquella que puede tomar un número infinito de valores numéricos entre dos valores dados, incluso si esos dos valores son arbitrariamente cercanos. Se usan para describir atributos medibles; por ejemplo la estatura y el peso. Los valores que toma una variable continua pueden ser números racionales, números reales o números complejos, aunque este último caso es menos frecuente en estadística.
La característica principal de las variables continuas es que entre dos valores racionales o reales siempre se puede encontrar otro, y entre ese otro y el primero se puede hallar otro valor, y así indefinidamente.

Por ejemplo, supongamos la variable peso en un grupo donde el de mayor peso tiene 95 Kg y el de menor peso 48 Kg; ese sería el rango de la variable y el número de valores posibles es infinito.
Por ejemplo entre 50,00 kg y 50,10 kg puede estar 50,01. Pero entre 50,00 y 50,01 puede estar la medida 50,005. Eso es una variable continua. En cambio, si en las medidas posibles de peso se estableciera una precisión de un solo decimal entonces la variable usada sería discreta.
Las variables continuas pertenecen a la categoría de variables cuantitativas, porque tienen asociado un valor numérico. Con este valor numérico es posible realizar operaciones matemáticas que van desde aritméticas hasta los métodos del cálculo infinitesimal.
Índice del artículo
- 1 Ejemplos
- 2 Ejercicio de variables continuas
- 3 Ejercicio de distribución de probabilidad
- 4 Referencias
La mayor parte de las variables de la física son variables continuas, entre ellas podemos nombrar: longitud, el tiempo, la rapidez, la aceleración, la energía, la temperatura y otras.
En estadística se pueden definir diversos tipos de variables, tanto las cualitativas como las cuantitativas. Las variables continuas pertenecen a esta última categoría. Con ellas es posible realizar operaciones aritméticas y de cálculo.
Por ejemplo la variable h, correspondiente a las personas con estatura entre 1,50 m y 1,95 m, es una variable contínua.
Comparemos esta variable con esta otra: el número de veces que sale cara en el lanzamiento de una moneda, a la cual llamaremos n.
La variable n puede tomar valores entre 0 e infinito, sin embargo n no es una variable contínua ya que no puede tomar el valor 1,3 o 1,5, debido a que entre valores 1 y 2 no hay ningún otro. Este es un ejemplo de variable discreta.
Considérese el siguiente ejemplo: una máquina produce cerillos de fósforo y los empaca en su caja. Se definen dos variables estadísticas:
Variable 1: L= Longitud del cerillo.
Variable 2: N= Número de cerillos por caja.
La longitud del cerillo nominal es 5,0 cm con una tolerancia de 0,1 cm. El número de cerillos por caja es 50 con una tolerancia de 3.
a) Indique el rango de valores que pueden tomar L y N.
b) ¿Cuántos valores puede tomar L?
c) ¿Cuántos valores puede tomar n?
Diga en cada caso si se trata de una variable discreta o continua.
Los valores de L están comprendidos en el intervalo [5,0-0,1 ; 5,0+0,1]; es decir que el valor de L está en intervalo [4,9 cm ; 5,1 cm] y la variable L puede tomar infinitos valores entre estas dos medidas. Se trata entonces de una variable continua.
El valor de la variable n está en el intervalo [47; 53]. La variable n solo puede tomar 6 valores posibles en el intervalo de tolerancia, se trata entonces de una variable discreta.
Si además de ser continua, los valores que toma la variable tienen asociada una determinada probabilidad de ocurrencia, entonces se trata de una variable aleatoria continua. Es muy importante distinguir si la variable es discreta o es continua, ya que los modelos probabilísticos aplicables a unas y otras son diferentes.
Una variable aleatoria continua queda completamente definida cuando se conocen los valores que puede asumir, y la probabilidad que tiene cada uno de ellos de suceder.
La fábrica de cerillas las hace de tal forma que la longitud de los palitos siempre está entre los valores 4,9 cm y 5,1 cm, y cero fuera de estos valores. Existe la probabilidad de obtener un palito que mida entre 5,00 y 5,05 cm, aunque también podríamos extraer uno de 5.0003 cm. ¿Son igualmente probables estos valores?.
Solución
Supongamos que la densidad de probabilidad es uniforme. A continuación se listan las probabilidades de encontrar un fósforo con determinada longitud:
-Que un fósforo se encuentre en el rango [4,9 ; 5,1] tiene probabilidad = 1 (o del 100%), ya que la máquina no saca cerillas fuera de esos valores.
-Hallar un fósforo que esté entre 4,9 y 5,0 tiene probabilidad = ½=0,5 (50%), puesto que es la mitad del rango de longitudes.
-Y la probabilidad de que la cerilla tenga longitud entre 5,0 y 5,1 también es 0,5 (50%)
-Se sabe que no hay palitos de fósforo que tengan una longitud comprendida entre 5,0 y 5,2. Probabilidad: cero (0%).
Probabilidad de encontrar un palillo en un rango determinado
Ahora observemos las siguientes probabilidades P de obtener palitos cuya longitud esté comprendida entre l1 y l2:
P = (l2 -l1) /(Lmax – Lmin)
-P de que un cerillo tenga una longitud comprendida entre 5,00 y 5,05 se denota como P([5,00 ; 5,05]):
P([5,00 ; 5,05])=(5,05 – 5,00)/(5,1 – 4,9)= 0,05/0,2= ¼ = 0,25 (25%)
-P de que el cerrillo tenga longitud entre 5,00 y 5,01 es:
P([5,00 ; 5,01])=(5,00 – 5,01)/(5,1 – 4,9)= 0,01/0,2= 1/20 = 0,05 (5%)
-P de que el cerrillo tenga longitud entre 5,000 y 5,001 es aún menor:
P(5,000 ; 5,001)= 0,001/0,2 = 1/200=0,005 (0,5%)
Si seguimos disminuyendo el intervalo para acercarnos más y más a 5,00, la probabilidad que un palillo tenga exactamente 5,00 cm es cero (0%). Lo que sí tenemos es la probabilidad de encontrar un cerilla dentro de un rango determinado.
Probabilidad de encontrar varios palillos en un rango determinado
Si los eventos son independientes la probabilidad de que dos palillos estén en determinado rango es el producto de sus probabilidades.
-La probabilidad que dos palillos estén entre 5,0 y 5,1 es 0,5*0,5=0,25 (0,25%)
-La probabilidad que 50 palillos estén entre 5,0 y 5,1 es (0,5)^50=9×10^-16, es decir casi nula.
-La probabilidad que 50 palillos estén entre 4,9 y 5,1 es (1)^50= 1 (100%)
En el ejemplo anterior se hizo la suposición que la probabilidad es uniforme en el intervalo dado, sin embargo no siempre es así.
En el caso de la máquina real que produce los palillos, la posibilidad de que el palillo esté en el valor central es mayor a que esté en uno de los valores extremos. Desde el punto de vista matemático esto se modela con una función f(x) conocida como densidad de probabilidad.
La probabilidad que la medida L este comprendida entre a y b se calcula mediante la integral definida de la función f(x) entre a y b.
Como ejemplo supongamos que queremos encontrar la función f(x), que representa una distribución uniforme entre los valores 4,9 y 5,1 del ejercicio 1.
Si la distribución de probabilidad es uniforme, entonces f(x) es igual a la constante c, que se determina tomando la integral entre 4,9 y 5,1 de c. Como esta integral es la probabilidad, entonces el resultado ha de ser 1.

Lo que significa que c vale 1/0,2= 5. Es decir la función densidad de probabilidad uniforme es f(x)={5 si 4,9≤x≤5,1 y 0 fuera de este rango. En la figura 2 se muestra una función de densidad de probabilidad uniforme.
Nótese como en intervalos del mismo ancho (por ejemplo 0,02) la probabilidad es la misma en el centro que en extremo del rango de la variable continua L (largo de palillo).
Un modelo más realista sería una función de densidad de probabilidad como el siguiente:
-f(x)=-750((x-5,0)^2-0,01) si 4,9≤x≤5,1
-0 fuera de este rango
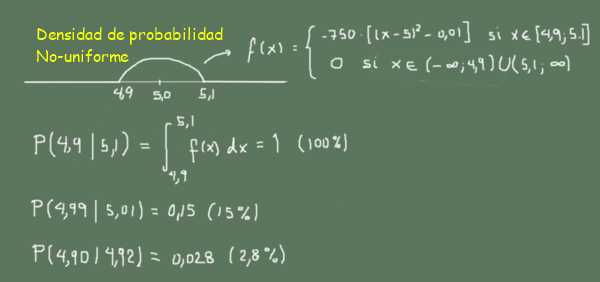
En la figura 3 puede observarse como la probabilidad de encontrar palillos entre 4,99 y 5,01 (ancho 0,02) es mayor que la de encontrar palillos entre 4,90 y 4,92 (ancho 0,02)
- Dinov, Ivo. Discrete Random Variables and Probability Distributions. Recobrado de: stat.ucla.edu
- Discrete and Continuous Random Variables. Recobrado de: ocw.mit.edu
- Discrete Random Variables and Probability Distributions. Recobrado de: homepage.divms.uiowa.edu
- H. Pishro. Introduction to Probability. Recuperado de: probability course.com
- Mendenhall, W. 1978. Estadística para Administración y Economía. Grupo Editorial Iberoamericana. 103-106.
- Problemas de Variables Aleatorias y Modelos de Probabilidad. Recobrado de: ugr.es.
- Wikipedia. Variable continua. Recuperado de wikipedia.com
- Wikipedia. Variable estadísticas. Recuperado de wikipedia.com.
