Ventaja mecánica: fórmula, ecuaciones, cálculo y ejemplos

La ventaja mecánica es el factor adimensional que cuantifica la capacidad de un mecanismo para amplificar -en algunos casos disminuir- la fuerza que se ejerce a través de él. El concepto se aplica para cualquier mecanismo: desde unas tijeras hasta el motor de un auto deportivo.

La idea es que una maquinaria transforme la fuerza que el usuario aplica sobre ella en una fuerza mucho mayor que represente provecho, o bien reducirla para llevar a cabo una tarea delicada.

Hay que tener presente que al accionar un mecanismo, una parte de la fuerza aplicada inevitablemente se invierte en contrarrestar el rozamiento. Por eso la ventaja mecánica se clasifica en ventaja mecánica real y ventaja mecánica ideal.

Índice del artículo

• 1 Definición y fórmulas
• 2 Ventaja mecánica ideal VMI
  • 2.1 Eficiencia o rendimiento de una máquina
• 3 Ventaja mecánica real VMR
  • 3.1 Relación entre VMI, VMR y la eficiencia
  • 3.2 Cálculo de VMR conociendo la eficiencia
• 4 ¿Cómo se calcula la ventaja mecánica?
• 5 Ejemplos
  • 5.1 – Ejemplo 1
  • 5.2 – Ejemplo 2
• 6 Referencias

Definición y fórmulas

La ventaja mecánica real de una máquina se define como la razón entre la magnitud de la fuerza ejercida por la máquina sobre la carga (fuerza de salida) y la fuerza requerida para operar la máquina (fuerza de entrada):

Ventaja mecánica real VMR = Fuerza de salida/Fuerza de entrada

Mientras que por su parte, la ventaja mecánica ideal depende de la distancia que recorre la fuerza de entrada y la que recorre la fuerza de salida:

Ventaja mecánica ideal VMI = Distancia de entrada/Distancia de salida

Al ser cocientes entre cantidades con las mismas dimensiones, ambas ventajas son adimensionales (sin unidades) y además positivas.

En muchos casos, como la carretilla y prensa hidráulica, la ventaja mecánica es mayor que 1, y en otros, la ventaja mecánica es menor que 1, por ejemplo en la caña de pescar y las pinzas.

Ventaja mecánica ideal VMI

La VMI está relacionada con el trabajo mecánico que se lleva a cabo en la entrada y en la salida de una máquina. El trabajo a la entrada, al que llamaremos W_i, se desglosa en dos componentes:

W_i = Trabajo para vencer la fricción + Trabajo de salida

Una máquina ideal no necesita hacer trabajo para vencer la fricción, por lo tanto el trabajo a la entrada sería el mismo que el de la salida, denotado como W_o:

Trabajo a la entrada = Trabajo a la salida →W_i = W_o.

Puesto que en este caso el trabajo es fuerza por distancia, se tiene: W_i = F_i . s_i

Donde F_i y s_i son respectivamente la fuerza y la distancia iniciales. El trabajo de salida se expresa de manera análoga:

W_o=F_o . s_o

En este caso F_o y s_o son la fuerza y la distancia que la maquinaria entrega, respectivamente. Ahora se igualan ambos trabajos:

F_i . s_i =   F_o . s_o

Y el resultado se puede reescribir en forma de cocientes de fuerzas y distancias:

(s_i /s_o) = (F_o /F_i)

Precisamente el cociente de distancias es la ventaja mecánica ideal, de acuerdo a la definición dada al comienzo:

VMI = s_i /s_o

Eficiencia o rendimiento de una máquina

Es razonable pensar en la eficiencia de la transformación entre ambos trabajos: el de la entrada y el de salida. Denotando como e a la eficiencia, esta se define como:

e = Trabajo de salida /Trabajo de entrada = W_o /W_i = F_o . s_o / F_i . s_i

A la eficiencia también se la conoce como rendimiento mecánico. En la práctica el trabajo de salida nunca supera al de entrada a causa de las pérdidas por fricción, por lo tanto el cociente dado por e ya no es igual a 1, sino menor.

Una definición alternativa involucra la potencia, que es el trabajo realizado por unidad de tiempo:

e = Potencia de salida /Potencia de entrada = P_o /P_i

Ventaja mecánica real VMR

La ventaja mecánica real se define simplemente como el cociente entre la fuerza de salida F_o y la de entrada F_i:

VMR = F_o/F_i

Relación entre VMI, VMR y la eficiencia

La eficiencia e puede reescribirse en términos de VMI y VMR:

e = F_o . s_o / F_i . s_i  = (F_o /F_i).(s_o/s_i) = VMR /VMI

Por lo tanto la eficiencia es el cociente entre la ventaja mecánica real y la ventaja mecánica ideal, siendo la primera menor que la segunda.

Cálculo de VMR conociendo la eficiencia

En la práctica, la VMR se calcula determinando la eficiencia y conociendo la VMI:
VMR = e. VMI

¿Cómo se calcula la ventaja mecánica?

El cálculo de la ventaja mecánica depende del tipo de maquinaria. En algunos casos conviene llevarlo a cabo mediante la transmisión de las fuerzas, pero en otro tipo de máquinas, como las poleas por ejemplo, es el torque o momento de torsión τ lo que se transmite.

En este caso, la VMI se calcula igualando los momentos:

Momento de torsión de salida = Momento de torsión de entrada

La magnitud del momento de torsión es τ = F.r.sen θ. Si la fuerza y el vector de posición son perpendiculares, entre ambos hay un ángulo de 90º y sen θ  = sen 90º = 1, obteniéndose:

F_o . r_o = F_i . r_i

En mecanismos como la prensa hidráulica, que consta de dos cámaras interconectadas por un tubo transversal y llenas de un fluido, se puede transmitir presión mediante pistones que se mueven libremente en cada cámara. En ese caso, la VMI se calcula mediante:

Presión en la salida = Presión en la entrada

Ejemplos

– Ejemplo 1

La palanca consiste en una barra delgada apoyada en un soporte llamado fulcro, que puede posicionarse de varias formas. Al aplicar una cierta fuerza, llamada “fuerza de potencia”, se vence con ella una mucho mayor, que es la carga o resistencia.

Hay varias formas de ubicar el fulcro, la fuerza de potencia y la carga para conseguir una ventaja mecánica. En la figura 3 se muestra la palanca de primera clase, semejante a un balancín, con el fulcro ubicado entre la fuerza de potencia y la carga.

Por ejemplo, dos personas de diferente peso pueden estar en equilibrio en el balancín o sube y baja si se sientan a distancias adecuadas del fulcro.

Para calcular la VMI de la palanca de primer grado, puesto que no hay traslación ni se consideran rozamientos, pero sí rotación, se igualan los momentos, sabiendo que ambas fuerzas son perpendiculares a la barra. Aquí F_i es la fuerza de potencia y F_o es la carga o resistencia:

F_o . r_o = F_i . r_i

F_o /F_i  = r_i / r_o

Por definición VMI = F_o /F_i , entonces:

VMI = r_i / r_o

En ausencia de rozamientos: VMI =VMR. Nótese que VMI puede ser mayor o menor a 1.

– Ejemplo 2

La ventaja mecánica ideal de la prensa hidráulica se calcula a través de la presión, que según el principio de Pascal, se transmite íntegramente a todos los puntos del fluido confinado en el recipiente.

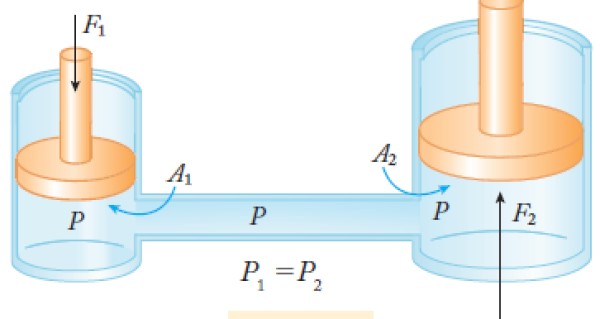
La fuerza de entrada F₁ en la figura 2, se aplica en el pistón pequeño de área A₁ a la izquierda, y la fuerza de salida F₂ se obtiene en el pistón grande de área A₂ a la derecha. Entonces:

Presión de entrada = Presión de salida

La presión se define como fuerza por unidad de área, por lo tanto:

(F₁ / A₁) = (F₂ / A₂) → A₂ / A₁  = F₂ / F₁ 

Dado que VMI = F₂ / F₁, se tiene la ventaja mecánica a través del cociente entre las áreas:

VMI = A₂ / A₁

Como A₂ > A₁, la VMI es mayor que 1 y el efecto de la prensa es multiplicar la fuerza aplicada en el pistón pequeño F₁.

Referencias

1. Cuéllar, J. 2009. Física II. 1ra. Edición. McGraw Hill.
2. Kane, J. 2007. Física. 2da. Edición. Editorial Reverté.
3. Tippens, P. 2011. Física: Conceptos y Aplicaciones. 7ma Edición. McGraw Hill
4. Wikipedia. Palanca. Recuperado de: es.wikipedia.org.
5. Wikipedia. Ventaja mecánica. Recuperado de: es.wikipedia.org.