Ley de Ohm: unidades y fórmula, cálculo, ejemplos, ejercicios
La ley de Ohm, en su forma macroscópica, señala que el voltaje y la intensidad de la corriente en un circuito son directamente proporcionales, siendo la resistencia la constante de proporcionalidad. Denotando a estas tres magnitudes como V, I y R respectivamente, la ley de Ohm establece que: V = I.R.
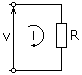
Asimismo, la ley de Ohm se generaliza para incluir elementos de circuito que no son puramente resistivos en circuitos de corriente alterna, de esta manera adopta la siguiente forma: V = I. Z.

Donde Z es la impedancia, que igualmente representa la oposición al paso de la corriente alterna por parte de un elemento de circuito, por ejemplo un condensador o una inductancia.
Hay que señalar que no todos los materiales y elementos de circuito cumplen con la ley de Ohm. A aquellos en los cuales es válida se denominan elementos óhmicos, y en los que no se cumple, son llamados no-óhmicos o no lineales.
Las resistencias eléctricas comunes son de tipo óhmico, pero los diodos y los transistores no lo son, ya que la relación entre voltaje y corriente no es lineal en ellos.
La ley de Ohm debe su nombre al físico y matemático alemán nacido en Baviera George Simon Ohm (1789-1854), quien se dedicó durante su carrera a estudiar el comportamiento de los circuitos eléctricos. En su honor se ha nombrado la unidad para resistencia eléctrica en el Sistema Internacional SI: el ohm, que también se expresa por la letra griega Ω.
Índice del artículo
Aunque la forma macroscópica de la ley de Ohm es la más conocida, ya que vincula cantidades que son fácilmente medibles en el laboratorio, la forma microscópica relaciona dos importantes cantidades vectoriales: el campo eléctrico E y la densidad de corriente J:
J = σ.E
Donde σ es la conductividad eléctrica del material, una propiedad que indica la facilidad que tiene para conducir corriente. Por su parte J es un vector cuya magnitud es el cociente entre la intensidad de corriente I y el área de la sección transversal A por la cual circula.
Es lógico suponer que existe una conexión natural entre el campo eléctrico en el interior de un material y la corriente eléctrica que circula por él, tal que a mayor más corriente.
Pero la corriente no es un vector, ya que no posee una dirección en el espacio. En cambio el vector J es perpendicular –o normal- al área de sección transversal del conductor y su sentido es el de la corriente.
A partir de esta forma de la ley de Ohm se llega a la primera ecuación, suponiendo un conductor de longitud ℓ y sección transversal A, y sustituyendo las magnitudes de J y E por:
J = I/A
E= V/ℓ
J = σ.E → I/A = σ. (V/ℓ)
V =( ℓ/σ.A).I
Al inverso de la conductividad se le denomina resistividad y se denota con la letra griega ρ:
1/ σ = ρ
Por lo tanto:
V = (ρℓ/ A).I = R.I
En la ecuación V =(ρℓ/ A).I, la constante (ρℓ/ A) es la resistencia, por lo tanto:
R = ρℓ/ A
La resistencia del conductor depende de tres factores:
-Su resistividad ρ, propia del material con el que está fabricado.
-La longitud ℓ.
-El área A de su sección transversal.
A mayor ℓ, mayor resistencia, pues los portadores de corriente tienen más oportunidades de colisionar con las demás partículas en el interior del conductor y perder energía. Y por el contrario, a mayor A, más fácil es para los portadores de corriente moverse de manera ordenada por el material.
Finalmente, en la estructura molecular de cada material reside la facilidad con que una sustancia deja que pase la corriente eléctrica. Así por ejemplo, los metales como el cobre, el oro, la plata y el platino, con baja resistividad, son buenos conductores, mientras que la madera, la goma y el aceite no lo son, por eso tienen mayor resistividad.
He aquí dos ejemplos ilustrativos de la ley de Ohm.
Una sencilla experiencia ilustra la ley de Ohm, para ello se necesita un trozo de material conductor, una fuente de voltaje variable y un multímetro.
Entre los extremos del material conductor se establece un voltaje V que se debe ir variando poco a poco. Con la fuente de poder variable se pueden ir fijando los valores de dicho voltaje, los cuales se miden con el multímetro, así como también la corriente I que circula por el conductor.
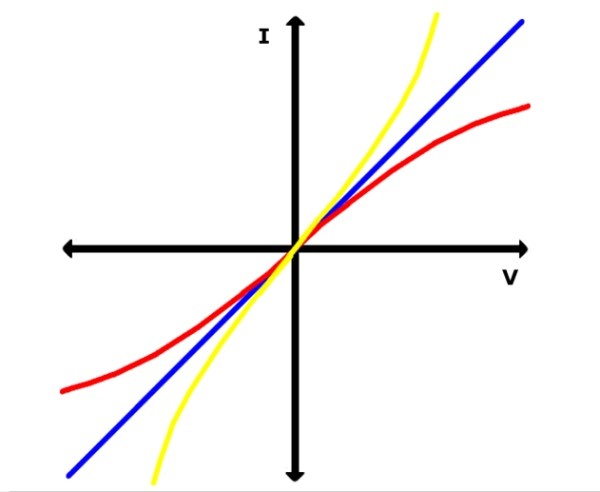
Las parejas de valores V e I se anotan en una tabla y con ellas se construye una gráfica sobre papel milimetrado. Si la curva resultante es una recta, el material es óhmico, pero si se trata de cualquier otra curva, el material es no óhmico.
En el primer caso, se puede determinar la pendiente de la recta, que equivale a la resistencia R del conductor o bien a su inverso, la conductancia.
En la siguiente imagen, la línea azul representa una de estas gráficas para un material óhmico. Mientras, las curvas amarilla y roja son de materiales no-óhmicos, como un semiconductor, por ejemplo.
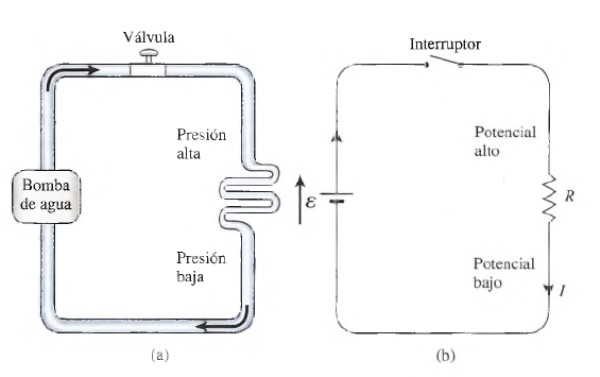
Es interesante saber que la corriente eléctrica en la ley de Ohm tiene un comportamiento parecido en cierta forma al del agua circulando por una tubería. El físico inglés Oliver Lodge fue el primero en proponer la simulación del comportamiento de la corriente mediante elementos de la hidráulica.
Por ejemplo las tuberías representan a los conductores, ya que por aquellas circula el agua y por los últimos los portadores de corriente. Cuando hay un estrechamiento en la tubería, se dificulta el paso de agua, así que esto equivaldría a una resistencia eléctrica.
La diferencia de presión en dos extremos del tubo permite que el agua fluya, la cual provee una diferencia de alturas o una bomba de agua, y de forma análoga, la diferencia de potencial (la batería) es la que mantiene a la carga en movimiento, equivalente al caudal o volumen de agua por unidad de tiempo.
Una bomba con pistón representaría el papel de una fuente de voltaje alterno, pero la ventaja de poner una bomba de agua es que así el circuito hidráulico estaría cerrado, tal como debe estar un circuito eléctrico para que fluya corriente.
Resistencias e interruptores
El equivalente de un interruptor en un circuito, vendría a ser una llave de paso. Se interpreta de esta manera: si el circuito está abierto (llave de paso cerrada), la corriente, lo mismo que el agua, no puede fluir.
En cambio, con el interruptor cerrado (llave de paso completamente abierta) tanto la corriente como el agua pueden circular sin problemas por el conductor o tubería.
La llave de paso o válvula también puede representar una resistencia: cuando la llave se abre completamente equivale a tener un a resistencia nula o cortocircuito. Si se cierra del todo es como tener el circuito abierto, mientras que cerrada parcialmente es como tener una resistencia de cierto valor (ver figura 3).
Se sabe que una plancha eléctrica requiere 2 A a 120 V para funcionar correctamente. ¿Cuál es su resistencia?
Solución
Se despeja la resistencia a partir de la ley de Ohm:
R = V/I = 120 V/ 2 A = 60 Ω
Un alambre de 3 mm de diámetro y 150 m de longitud posee resistencia eléctrica de 3.00 Ω a 20°C. Encuentre la resistividad del material.
Solución
La ecuación R = ρℓ/ A es apropiada, por lo tanto se necesita hallar primero el área de la sección transversal:
A = π(D/2)2 = π (3 x 10-3 m/2)2 = 4.5π x 10 -6 m2
Finalmente al sustituir se obtiene:
ρ = A.R /ℓ = 4.5π x 10 -6 m2 x 3 Ω / 150 m =2.83 x 10 -7 Ω.m
- Resnick, R. 1992.Física. Tercera edición ampliada en español. Volumen 2. Compañía Editorial Continental S.A. de C.V.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 2. 817-820.
- Serway, R., Jewett, J. 2009. Física para Ciencias e Ingeniería con Física Moderna. 7ma Edición. Volumen 2. Cengage Learning. 752-775.
- Tippens, P. 2011. Física: Conceptos y Aplicaciones. 7ma Edición. McGraw Hill.
- Universidad de Sevilla. Departamento de Física Aplicada III. Densidad e intensidad de corriente. Recobrado de: us.es.
- Walker, J. 2008. Physics. 4th Ed. Pearson.725-728
