Ley de Darcy: ecuaciones, aplicaciones, limitaciones, ejercicio
¿Qué es la ley de Darcy?
La ley de Darcy es una relación matemática aplicable al flujo de fluidos en medios permeables o porosos, por ejemplo, el agua que drena en la arena.
A medida que el fluido avanza por el medio poroso, su presión hidrostática va variando, específicamente es mayor en los puntos más cercanos a la fuente y menor en los puntos más cercanos al drenaje. De esta forma aparece el concepto de gradiente hidráulico, una cantidad física que se denotará con la letra I.
Por otra parte, el medio poroso se caracteriza por una cantidad llamada conductividad hidráulicaK. Claramente existe una relación entre la porosidad, determinada por K, el gradiente hidráulico I y el caudal por unidad de área de sección transversal q.
La relación entre ellas fue descubierta por el ingeniero hidráulico francés Henry Darcy (1803-1858), quien estuvo a cargo del suministro de agua de su ciudad natal: Dijon.
La ley de Darcy fue presentada en 1856, en un minucioso trabajo en el que se detalla las cantidades físicas involucradas en la ley, los experimentos realizados y muy particularmente, un aparato llamado permeámetro.
Ecuaciones de la ley de Darcy
La ley de Darcy muestra la relación entre varias cantidades físicas que describen el flujo a través de un medio poroso. En ella se indica que el caudal de agua Q que se mueve a través de un determinado medio poroso es directamente proporcional a la sección transversal atravesada A y al gradiente hidráulico I:
Q ∝ A∙I
La constante de proporcionalidad es la permeabilidad K del medio poroso, también llamada conductividad hidráulica. De esta manera, la ley de Darcy se presenta como:
Q = K∙A∙I
Forma diferencial de la ley de Darcy
La ecuación de Darcy se puede expresar como una relación diferencial entre la velocidad del flujo en cada punto y el gradiente hidráulico local:
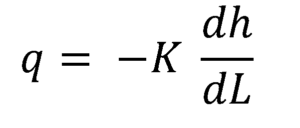
Como el gradiente hidráulico es una cantidad negativa cuando se calcula en la dirección del flujo, es necesario entonces multiplicar por el negativo de la conductividad hidráulica para obtener la velocidad de flujo medio q, en cada sección transversal.
Seguidamente se analiza con mayor detalle las magnitudes presentes en la ley de Darcy.
Caudal, gradiente hidráulico y permeabilidad
1.- Caudal Q
Se define el caudal como el volumen de agua que circula a través de una determinada área de sección transversal a la dirección del flujo, por unidad de tiempo:
Q = ΔV / Δt
En el Sistema Internacional de Unidades SI, el caudal se mide en metros cúbicos por segundo, pero frecuentemente se expresa también en litros por minuto o litros por segundo.
Con frecuencia se requiere el caudal por unidad de área q, que es el cociente entre el caudal Q y el área de sección transversal:
q = Q / A
En el SI, q se expresa en m/s, razón por la cual q representa la velocidad promedio del fluido en la sección transversal de la tubería.
Es importante destacar que, mientras el caudal Q es el mismo en todas las secciones de la tubería, el caudal por unidad de área q o simplemente la velocidad de flujo es mayor en las secciones más estrechas y menor en las más anchas.
2.- Gradiente hidráulico I
Cuando un fluido circula a lo largo de un medio poroso, la presión hidrostática decrece en la misma dirección del flujo.
Se sabe que la presión hidrostática, en un determinado punto de la tubería, es proporcional a la altura h que marca un manómetro de tubo abierto en ese lugar. La constante de proporcionalidad es el producto de la densidad del fluido por la aceleración de gravedad.
De esta manera, se define el gradiente hidráulico I como el cociente entre la diferencia de altura Δh de las columnas de dos manómetros y ΔL, siendo esta última cantidad la distancia que separa los manómetros (ver la figura abajo):
I = Δh / ΔL
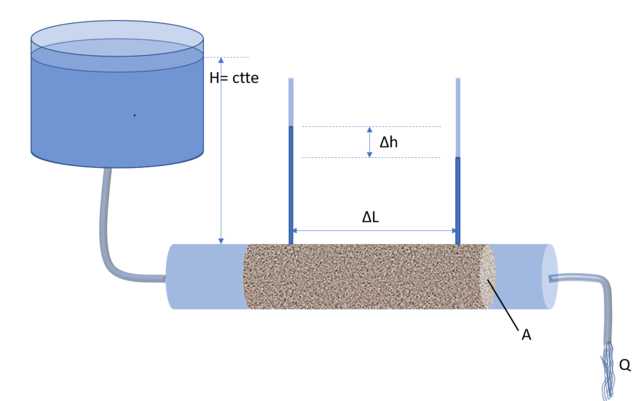
Este es el gradiente hidráulico medio en el tramo de largo ΔL, una cantidad adimensional y además negativa.
Si se quiere hallar el gradiente hidráulico en cada punto de la tubería, se toma el límite para ΔL tendiendo a cero, dando como resultado la derivada de la función gradiente hidráulico respecto de la posición L, a lo largo del flujo:
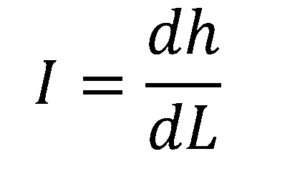
3.- Permeabilidad K
La permeabilidad de un medio poroso o conductividad hidráulica K es el cociente entre el caudal Q y el producto de la sección transversal de área A por el gradiente hidráulico I:
K = Q / A∙I
La conductividad hidráulica tiene unidades de velocidad, metros sobre segundo en SI.
Se ha definido una unidad para K, llamada darcy, en honor a Henry Darcy y definida así:
Un darcy es la permeabilidad de un mililitro de fluido, con viscosidad de un centipoise, que se mueve a lo largo de un centímetro en una presión diferencial de una atmósfera, a través de una sección transversal de un centímetro cuadrado.
Aplicaciones de la ley de Darcy
La principal aplicación de la ley de Darcy consiste en predecir el flujo de agua a lo largo de un acuífero, antes de efectuar la perforación de los pozos.
Asimismo, la ley de Darcy es usada regularmente en la ingeniería agrícola e hidrológica. También puede emplearse en la industria petrolera para describir el flujo de gas y petróleo en medios porosos. No obstante, en ese caso K puede variar, según el flujo sea de gas o de petróleo y puede que no dependa única y exclusivamente del sustrato permeable.
Limitaciones
La ley de Darcy supone que la conductividad hidráulica K es una cantidad propia del medio, lo cual es cierto en muchos casos. Sin embargo, a veces K depende de la viscosidad dinámica del fluido, la cual a su vez puede depender de la velocidad del flujo y de los gradientes de temperatura.
La suposición de Darcy es plausible cuando se considera el flujo de agua subterránea, donde la viscosidad es prácticamente constante, ya que su valor casi no se ve afectado en vista de las pocas diferencias de temperatura a lo largo de acuífero.
En los casos del flujo de petróleo a través de medios porosos, la ecuación de Darcy no puede aplicarse tal como se ha presentado acá, sino que se incorporan ciertas modificaciones que van más allá del propósito del este artículo.
Ejercicio resuelto
Determinar la conductividad hidráulica de una arena de playa, mediante el uso de un permeámetro de laboratorio.
Supóngase que el tubo del permeámetro tiene un diámetro de 20 cm y que la distancia entre los dos manómetros es de 50 cm. También se conoce que el agua fluye a razón de 300 decímetros cúbicos por minuto y la diferencia de nivel entre los dos manómetros es de 25 cm.
Solución
El caudal Q es 300 decímetros cúbicos por minuto, pero expresando en unidades del sistema internacional quedaría así:
Q = 300 x 10-3 m3 / 60 s = 5 x 10-3 m3 / s
La sección transversal de área A se calcula mediante:
A = π∙R2 = π∙(10 cm)2 = π∙(0,1 m)2 = 0,314 m2
El gradiente hidráulico I es cociente entre la diferencia de altura manométrica y la separación de los manómetros:
I = 25 cm / 50 cm = 0,5
Según la definición de la conductividad hidráulica K dada anteriormente:
K = Q / A∙I = ( 5 x 10-3 m3 / s) / (0,314 m2 ∙0,5) = 3,185 x 10-2 m/s ≈ 2 m/min.
