Geometría analítica: qué es, qué estudia, historia, aplicaciones

¿Qué es la geometría analítica?

La geometría analítica es la rama de las matemáticas en la que se combinan la geometría y el álgebra, para resolver diversos problemas geométricos a través de técnicas algebraicas.

Utiliza como base los sistemas de coordenadas, tal como el sistema de coordenadas cartesiano, que debe su nombre justamente a René Descartes. De esta manera, es posible asociar curvas en el plano y en el espacio, con ecuaciones algebraicas.

Un ejemplo de ello es la conocida ecuación de la circunferencia de radio R centrada en el origen del sistema de coordenadas:

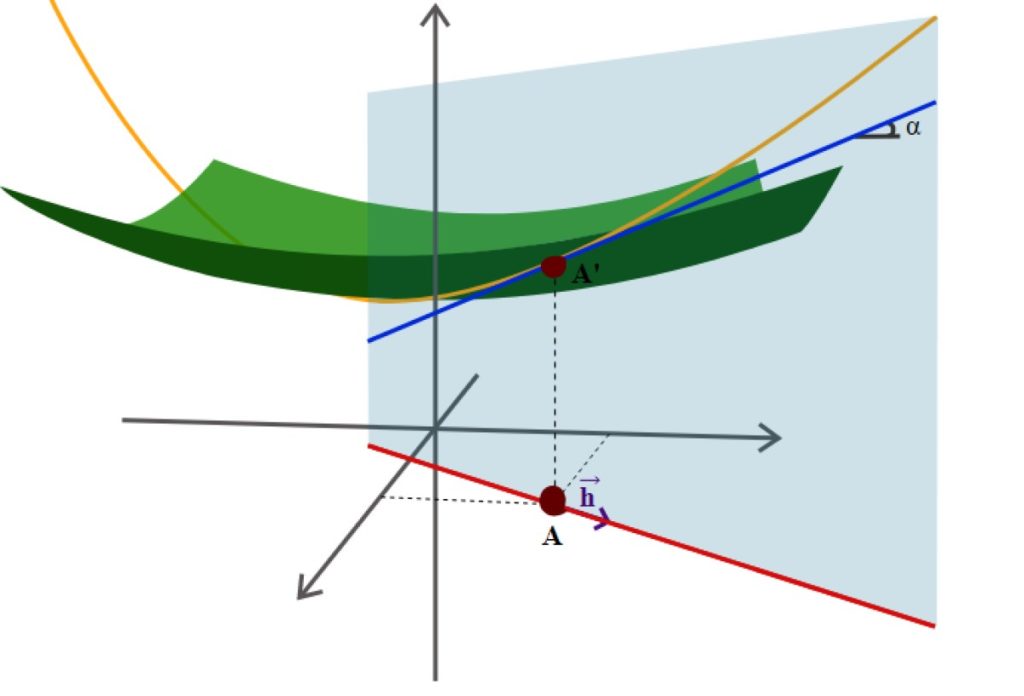
De igual forma, a través de la geometría analítica, es posible el trazado de gráficas de funciones. Y como es sabido, las funciones permiten el modelado de problemas de ciencia e ingeniería. Por ello, la geometría analítica se encuentra presente en los planes de estudio de las carreras asociadas a estas áreas del saber.

Historia breve de la geometría analítica

La geometría analítica tiene su origen en la primera mitad del siglo XVII, de la mano de dos notables matemáticos franceses: René Descartes (1596-1650) y Pierre de Fermat (1601-1665).

Sin embargo, puede decirse que sus antecedentes se remontan siglos atrás, al matemático griego Apolonio de Pérgamo (262-190 a.C.). Él escribió un tratado sobre las cónicas, a las que otorgó sus nombres: circunferencia, elipse, parábola e hipérbola.

Así, la obra de Apolonio fue la base para que, mucho después, los franceses René Descartes y Pierre de Fermat sentaran las bases de la geometría analítica, de manera independiente. Pero Descartes es considerado el padre de esta ciencia, pues fue el primero en publicar sus trabajos.

Descartes, Fermat y Euler

En El Discurso del Método de 1637, Descartes unificó dos disciplinas que hasta entonces habían estado separadas: el álgebra y la geometría. En su obra, Descartes introduce el sistema de coordenadas cartesiano, para ubicar puntos en el plano y en el espacio.

Asimismo, hace uso de ecuaciones algebraicas de segundo grado con dos variables, para describir las secciones cónicas y se dedica a resolver problemas geométricos con ellas. También de crear buena parte de la notación matemática que se emplea actualmente.

A Pierre de Fermat se le asocia más con la óptica que con la geometría analítica, sin embargo, sus aportaciones son notables.

En 1629, Fermat retomó las cónicas de Apolonio de Pérgamo y creó las técnicas que conforman la geometría analítica, inventando un sistema de coordenadas propio y definiendo claramente el concepto clave de lugar geométrico, con el que se inicia el estudio de la geometría analítica.

Sin embargo, los trabajos de Fermat no vieron la luz sino hasta 1679, publicados por su hijo, cuando ya el matemático había fallecido. Por este motivo, se le atribuye a Descartes la paternidad de la geometría analítica.

Posteriormente a los matemáticos franceses, el suizo Leonardo Euler (1707-1783) estableció las bases formales de la geometría analítica. Euler introdujo varios sistemas de coordenadas en el plano y el espacio: las coordenadas rectangulares, polares y oblicuas, así como las transformaciones de uno a otro sistema.

En sus trabajos acerca de la geometría analítica, Euler también profundizó en la clasificación de diversas curvas, según el grado de la ecuación algebraica representativa (tercer y cuarto orden) y estudió sus propiedades de manera intensiva, las ecuaciones de las tangentes, las curvaturas, las simetrías y mucho más.

¿Qué estudia la geometría analítica?

A grandes rasgos, la geometría analítica se centra en el estudio de los elementos geométricos, como puntos, segmentos, rectas, curvas, superficies y volúmenes. Para ello, como se dijo anteriormente, establece ecuaciones algebraicas que describen y relacionan estos elementos, permitiendo su manejo a través de técnicas algebraicas.

Los principales objetivos de la geometría analítica, de forma muy resumida, son los siguientes:

1. Establecer el sistema de coordenadas cartesianas y el sistema de coordenadas polares, para ubicar puntos en el plano, así como su extensión a puntos en el espacio.
2. Trazar segmentos, rectas, curvas y superficies sobre el plano cartesiano y el espacio.
3. Deducir las ecuaciones que describen analíticamente una curva y la construcción de la misma sobre el plano y/o el espacio, así como el estudio de todas sus propiedades.
4. Clasificar curvas, superficies y volúmenes.
5. Derivar fórmulas fundamentales para resolver problemas sobre puntos notables, rectas, planos, ángulos, paralelismo, perpendicularidad, distancias, intersecciones, áreas y más.
6. Resolver problemas geométricos mediante la aplicación de métodos algebraicos, para lo cual se deducen fórmulas referentes a puntos notables, ecuaciones para la recta, los planos, los ángulos, distancia entre puntos, entre rectas y puntos, puntos de tangencia, rectas secantes, áreas y mucho más.
7. Trabajar con espacios vectoriales y productos entre vectores.

Distancia entre dos puntos

Como ejemplo de las numerosas aplicaciones de la geometría analítica, uno de los más sencillos es el cálculo de la distancia entre dos puntos del plano. Sean dos puntos P₁ y P₂, de coordenadas (x₁,y₁) y (x₂,y₂) respectivamente, la distancia d entre ellos se calcula mediante:

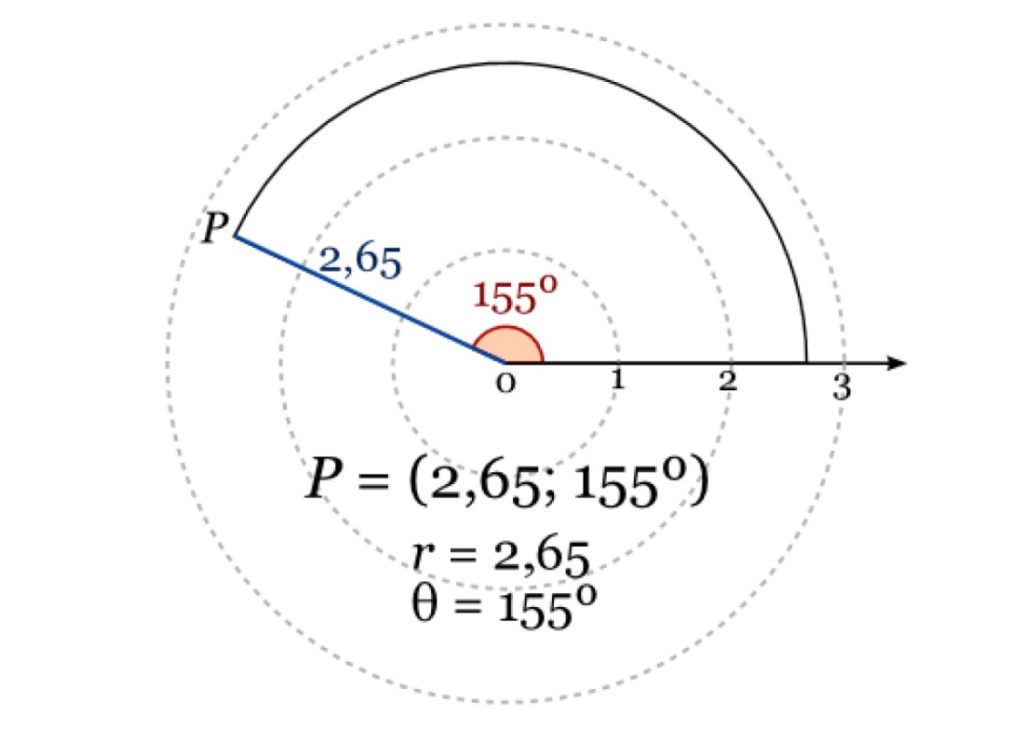
Coordenadas polares

Un punto del plano se puede especificar a través de su distancia “r” al origen del sistema de coordenadas, llamado polo, y el ángulo que forma la recta que contiene al punto y al polo, con el eje horizontal o eje polar.

Aplicaciones de la geometría analítica

Fundamento del Cálculo infinitesimal

La geometría analítica es fundamental para el desarrollo del Cálculo infinitesimal, ya que facilita la representación gráfica de curvas y funciones, y trabajar con estas de manera analítica, para crear modelos que representen fenómenos de la naturaleza.

Mapas

El sistema de coordenadas cartesianas ayuda a elaborar mapas e identificar lugares mediante latitud y longitud, equivalentes a las coordenadas cartesianas de un punto en el plano.

Cálculos topográficos

Distintos tipos de sistemas de coordenadas se emplean en topografía y constituyen la base de su estudio y aplicaciones. Entre ellos está el sistema de coordenadas polares antes descrito.

Trayectorias de cuerpos celestes

Las secciones cónicas, descritas a través de la geometría analítica, participan en importantes fenómenos de la naturaleza, tal como las trayectorias de los cuerpos celestes, sujetos a la fuerza de la gravedad. Por ejemplo, los planetas y algunos cometas describen trayectorias elípticas alrededor del Sol, con este ubicado en uno de los focos.

Arquitectura y construcciones civiles

Numerosas curvas forman parte de las construcciones arquitectónicas, por ejemplo, los cables de un puente colgante pueden tomar la forma de parábolas.

Sistemas de posicionamiento global

El sistema de posicionamiento global o GPS hace posible ubicar localidades con precisión, así como objetos en movimiento, como vehículos y embarcaciones. También ayuda a las personas a llegar con más facilidad a sus destinos, guiándolas por las mejores rutas.