¿Qué es un geoide?
El geoide o figura de la Tierra es la superficie teórica de nuestro planeta, determinada por el nivel medio de los océanos y con una forma bastante irregular. Matemáticamente se define como la superficie equipotencial del potencial gravitatorio efectivo de la Tierra, a nivel del mar.
Como se trata de una superficie imaginaria (no material), atraviesa continentes y montañas, como si todos los océanos estuviesen conectados por canales acuáticos que pasan a través de las masas terrestres.

La Tierra no es una esfera perfecta, ya que la rotación alrededor de su eje la convierte en una especie de balón achatado por los polos, con valles y montañas. Por eso la forma de esferoide todavía sigue siendo inexacta.
Esa misma rotación añade a la fuerza de gravedad terrestre una fuerza centrífuga, cuya resultante o fuerza efectiva no apunta al centro de la Tierra, pero tiene asociado un cierto potencial gravitatorio.
Sumado a esto los accidentes geográficos crean irregularidades en la densidad, y por lo tanto la fuerza de atracción gravitacional en algunas zonas definitivamente deja de ser central.
Por eso los científicos, comenzando por C. F. Gauss, quien ideó el geoide original en 1828, crearon un modelo geométrico y matemático para representar la superficie terrestre con mayor precisión.
Para ello se supone un océano en reposo, sin mareas ni corrientes oceánicas y con densidad constante, cuya altura sirva como referencia. Después se considera que la superficie de la Tierra ondula suavemente, elevándose en los lugares donde la gravedad local es mayor y hundiéndose cuando esta disminuye.
En estas condiciones hagamos que la aceleración de gravedad efectiva sea siempre perpendicular a la superficie cuyos puntos estén al mismo potencial y el resultado es el geoide, que es irregular dado que la equipotencial no es simétrica.
Índice del artículo
- 1 Fundamento físico del geoide
- 2 Diferencias entre el geoide y el elipsoide
- 3 Ventajas de representar a la Tierra como un geoide
- 4 Referencias
Para determinar la forma del geoide, que se ha ido refinando con el tiempo, los científicos han llevado a cabo muchas medidas, tomando en cuenta dos factores:
– El primero es que el valor de g, el campo gravitatorio terrestre equivalente a la aceleración de la gravedad, depende de la latitud: es máximo en los polos y mínimo en el ecuador.
– El segundo es que, como ya dijimos antes, la densidad de la Tierra no es homogénea. Hay lugares en los que aumenta porque las rocas son más densas, existe una acumulación de magma o hay mucho terreno sobre la superficie, como una montaña por ejemplo.
Donde la densidad es mayor, g también lo es. Nótese que g es un vector y por eso se lo denota con negrita.
Para definir el geoide se necesita el potencial debido a la gravedad, para lo cual hay que definir el campo gravitatorio como la fuerza gravitatoria por unidad de masa.
Si una masa de prueba m se coloca en dicho campo, la fuerza que ejerce la Tierra sobre ella es su peso P = mg, por lo tanto la magnitud del campo es:
Fuerza / masa = P /m = g
Ya conocemos su valor medio: 9.8 m/s2 y si la Tierra fuera esférica, estaría dirigido hacia su centro. Análogamente, de acuerdo a la ley de gravitación universal de Newton:
P = Gm M /r2
Donde M es la masa de la Tierra y G es la constante de gravitación universal. Entonces la magnitud del campo gravitatorio g es:
g = GM/r2
Se parece mucho a un campo electrostático, por lo que se puede definir un potencial gravitatorio que sea análogo al electrostático:
V = -GM/r
La constante G es la constante de gravitación universal. Pues bien, las superficies sobre las cuales el potencial gravitatorio siempre tiene el mismo valor se llaman superficies equipotenciales y g siempre es perpendicular a ellas, como se dijo antes.
Para esta clase de potencial en particular, las superficies equipotenciales son esferas concéntricas. El trabajo requerido para mover una masa sobre ellas es nulo, debido a que la fuerza siempre es perpendicular a cualquier camino sobre la equipotencial.
Componente lateral de la aceleración de la gravedad
Como la Tierra no es esférica, la aceleración de gravedad debe tener una componente lateral gl debida a la aceleración centrífuga, causada por el movimiento de rotación del planeta alrededor de su eje.
En la siguiente figura se muestra en verde dicha componente, cuya magnitud es:
gl = ω2a
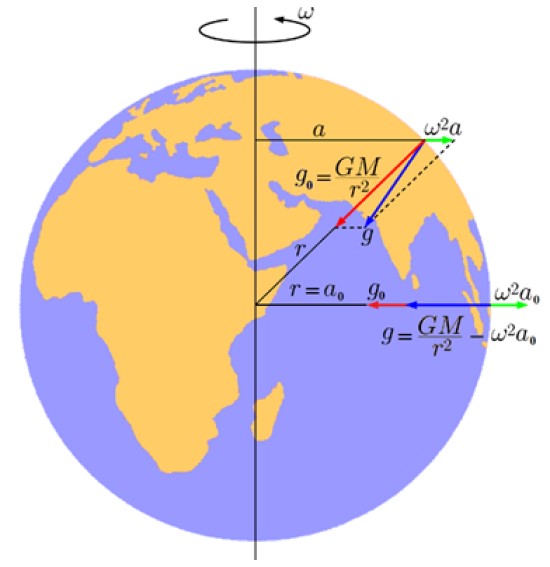
En esta ecuación ω es la velocidad angular de rotación de la Tierra y a es la distancia entre el punto sobre la Tierra, a cierta latitud y el eje.
Y en rojo está la componente que se debe a la atracción gravitacional planetaria:
go = GM/r2
Como resultado, al sumar vectorialmente go + gl, se origina una aceleración resultante g (en azul) que es la verdadera aceleración de gravedad de la Tierra (o aceleración efectiva) y que como vemos no apunta exactamente al centro.
Además, la componente lateral depende de la latitud: es nula en los polos y por eso allí el campo gravitatorio es máximo. En el ecuador se opone a la atracción gravitacional, reduciendo la gravedad efectiva, cuya magnitud queda:
g = GM/r2 – ω2R
Con R = radio ecuatorial de la Tierra.
Ahora se comprende que las superficies equipotenciales de la Tierra no sean esféricas, sino que adoptan una forma tal que g siempre sea perpendicular a ellas en todo punto.
Aquí está el segundo factor que incide en la variación del campo gravitatorio terrestre: las variaciones locales de la gravedad. Hay lugares en los que la gravedad aumenta porque hay más masa, por ejemplo en la colina de la figura a).
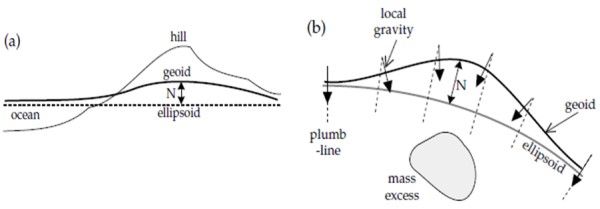
O existe una acumulación o exceso de masa por debajo de la superficie, como en b). En ambos casos se produce una elevación en el geoide porque a mayor masa, mayor intensidad del campo gravitatorio.
En cambio sobre el océano, la densidad es menor y como consecuencia el geoide se hunde, como vemos a la izquierda de la figura a), por encima del océano.
De la figura b) también se advierte que la gravedad local, señalada con flechas, siempre es perpendicular a la superficie del geoide, tal como hemos dicho. Esto no siempre ocurre con el elipsoide de referencia.
En la figura aparece señalada también, con una flecha bidireccional, la diferencia de altura entre el geoide y el elipsoide, la cual se denomina ondulación y se denota como N. Las ondulaciones positivas se relacionan con excesos de masa y las negativas con defectos.
Las ondulaciones no sobrepasan casi nunca los 200 m. En realidad, los valores dependen de cómo se escoge el nivel del mar que sirve como referencia, ya que algunos países eligen distinto según sus características regionales.
-Sobre el geoide el potencial efectivo, resultado del potencial debido a la gravedad y el potencial centrífugo, es constante.
-La fuerza de gravedad siempre actúa perpendicularmente al geoide y el horizonte siempre es tangencial a él.
-El geoide ofrece una referencia para aplicaciones cartográficas de gran precisión.
-Mediante el geoide los sismólogos pueden detectar la profundidad a la que ocurren los terremotos.
-El posicionamiento de los GPS depende del geoide a utilizar como referencia.
-La superficie del océano también va paralela al geoide.
-Las elevaciones y los descensos del geoide indican los excesos o defectos de masa, que son las anomalías gravimétricas. Cuando una anomalía es detectada y dependiendo de su valor, es posible inferir la estructura geológica del subsuelo, al menos hasta ciertas profundidades.
Este es el fundamento de los métodos gravimétricos en geofísica. Una anomalía gravimétrica puede indicar acumulaciones de ciertos minerales, estructuras enterradas bajo tierra, o también espacios vacíos. Los domos de sal en el subsuelo, detectables por métodos gravimétricos, son indicativos en algunos casos de la presencia de petróleo.
- ESA. Euronews. Gravity’s grip on Earth. Recuperado de: youtube.com.
- GOCE. Geoide. Recuperado de: youtube.com.
- Griem-Klee, S. Exploraciones mineras: gravimetría. Recuperado de: geovirtual2.cl.
- Lowrie, W. 2007. Fundamentals of Geophysics. 2nd. Edition. Cambridge University Press.
- NOAA. What is the geoid?. Recuperado de: geodesy.noaa.gov.
- Sheriff, R. 1990. Applied Geophysics. 2nd. Edition. Cambridge University Press.
