¿Qué es la directriz? (Geometría)
La directriz en geometría consiste en una curva, superficie o volumen que permanece fijo y determina la manera en que se forma un objeto geométrico. Por ejemplo, mediante una recta se establecen otras curvas como las cónicas, y las superficies de revolución, como el cilindro circular recto.
La curva directriz también puede ser una circunferencia. Un cilindro circular recto se puede formar dejando fija una circunferencia directriz de radio R.
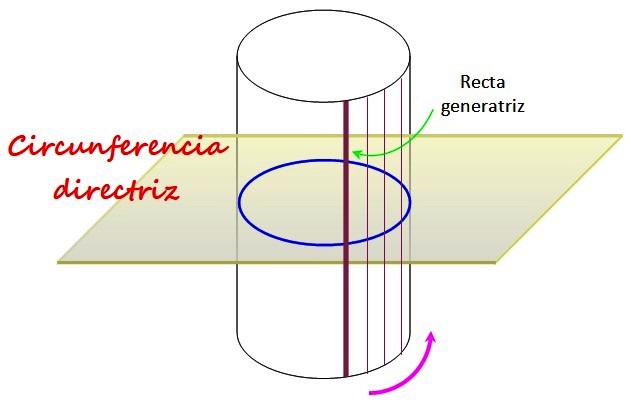
La circunferencia, que está sobre el plano dibujado en la figura, determina la forma de la superficie curva del cilindro circular recto, el cual se genera haciendo girar la recta a su alrededor, llamada recta generatriz.
Si la curva directriz no es una circunferencia, sino otra curva, se generan otros tipos de cilindro, como el cilindro elíptico, cuya directriz es una elipse.
Una circunferencia también puede actuar como directriz para generar otra curva, tal es el caso de la epitrocoide, una curva en el plano generada por un punto, que a su vez está en una circunferencia más pequeña que rueda sin deslizar, alrededor de la directriz.
Es más sencillo apreciarlo visualmente mediante la siguiente animación:
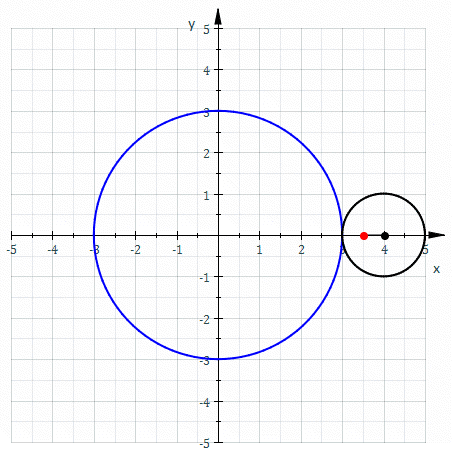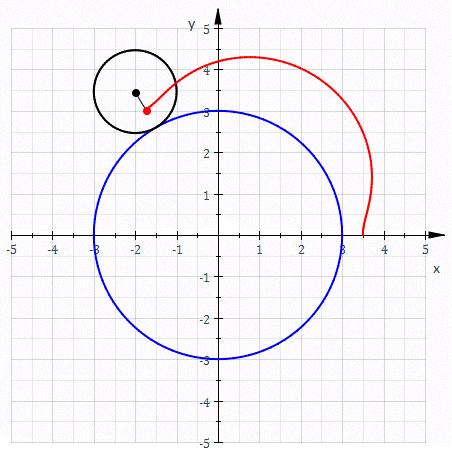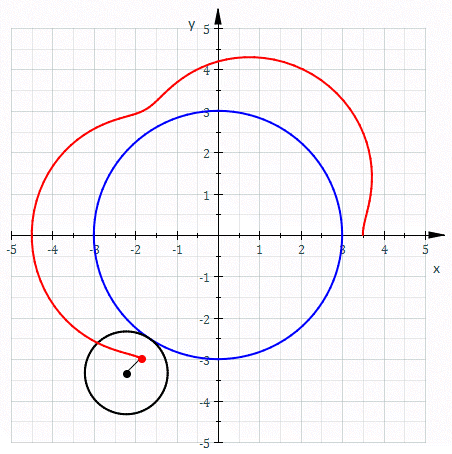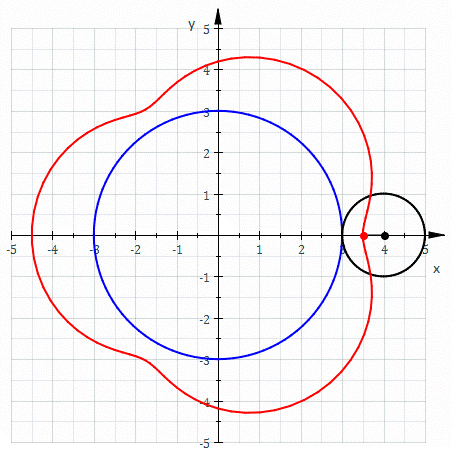
La curva directriz en las superficies cilíndricas
Las superficies cilíndricas se clasifican de acuerdo a su curva directriz en cilindros:
-Circulares
-Elípticos
-Parabólicos
-Hiperbólicos
Cuando una superficie cilíndrica tiene una directriz que yace en un plano perpendicular al de la recta generatriz, la ecuación de dicha superficie es la misma que la ecuación de la directriz.
Los cilindros pertenecen al grupo de las superficies cuádricas, cuya ecuación es de segundo grado con tres variables. La forma general es:
Ax2 + By2 + Cz2 + Dxy + Exz + Fyz +Gx + Hy + Iz + K = 0
Donde los coeficientes A, B, C… son números reales.
Los cilindros son los cuerpos geométricos tridimensionales más comunes y útiles que se pueden encontrar, sobre todo los cilindros circulares rectos, pero los demás tipos de cilindros que se describen a continuación también tienen aplicaciones en ingeniería y diseño.
Cilindro circular recto
Su directriz es una circunferencia C que se encuentra en un plano perpendicular al cilindro, tal como se muestra en la figura 1, ya que la recta generatriz, que recorre a C para formar la superficie lateral, es perpendicular a C.
La ecuación de la circunferencia C en el plano xy, centrada en el origen (0,0) es:
x2 + y2 = R2
Donde R, el radio de la circunferencia será, evidentemente, el radio del cilindro. La altura h del cilindro se extiende a lo largo del eje z, perpendicular al plano xy.
Cilindro elíptico
La directriz es una elipse en el plano xy centrada en el origen (0,0), cuya ecuación es:
La generatriz es una recta perpendicular al plano xy, que se mueve alrededor de la elipse para dar lugar a la superficie lateral. La elipse puede encontrarse a cualquier altura z sobre el plano xy.
Por ejemplo, la elipse de ecuación:
4x2 + 9y2 = 36
Es la curva directriz que da lugar al cilindro elíptico cuya ecuación es 4x2 + 9y2 = 36, más z=0. Añadiendo esta última expresión, se tiene claro que se trata de la superficie.
Cilindro parabólico
En este caso la curva directriz es una parábola, que puede ser de la forma y = x2. Así el cilindro está dirigido a lo largo del eje z y se forma apilando parábolas con vértice en (0,0) a lo largo de dicho eje.
El cilindro parabólico tiene aplicación en energía solar, ya que algunos colectores tienen espejos de esa forma, mediante la cual la luz del sol se concentra en el foco. Por este punto se hace pasar una tubería recta dentro de la cual un aceite alcanza temperaturas de hasta 400 º C.
Cilindro hiperbólico
En el cilindro hiperbólico, la ecuación de la directriz es la hipérbola centrada en el origen:
El cilindro se forma al apilar hipérbolas a lo largo del eje z.
Superficie de revolución
La curva directriz de una superficie de revolución es el mismo eje de revolución, la recta alrededor de la cual gira la curva que se encarga de generar la superficie.
La curva que gira puede tener forma arbitraria, de esta manera se genera una superficie como la que se ve en esta animación:
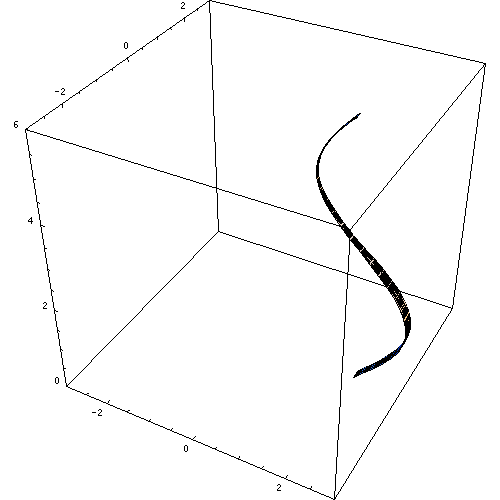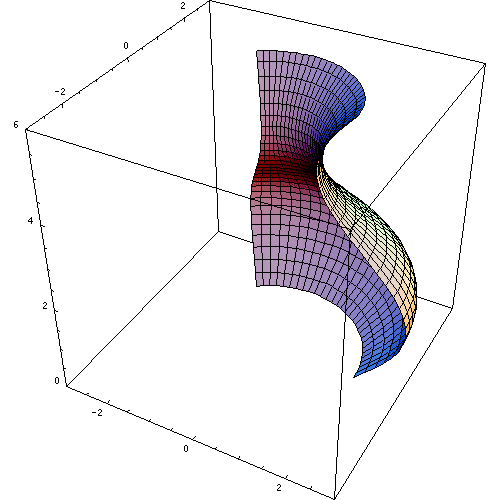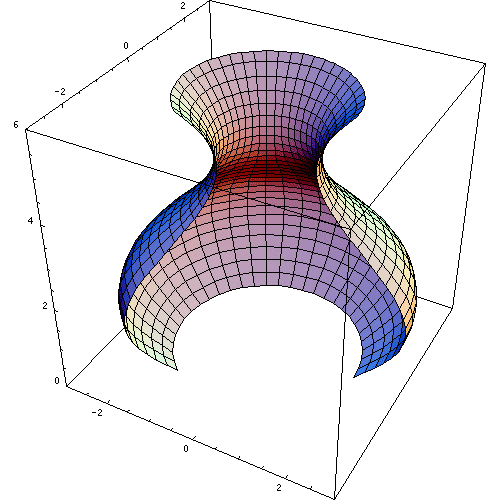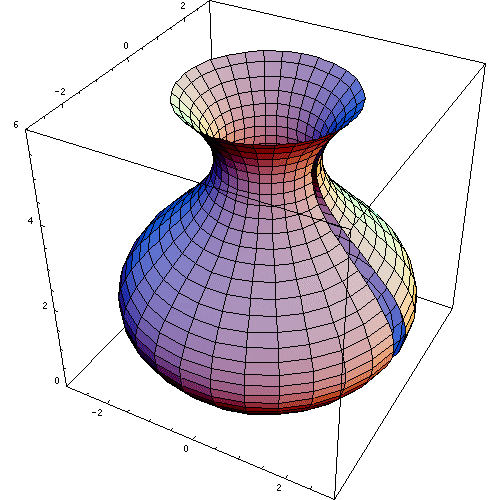
Si se hace girar otra recta alrededor de la recta directriz, se obtiene el ya familiar cilindro circular recto. De la misma forma se pueden obtener otras superficies de revolución, como por ejemplo superficies de revolución cónicas, esféricas y toroidales.
Superficie cónica
Una superficie cónica se genera mediante el movimiento de una recta generatriz que pasa siempre por la curva plana fija o curva directriz y por el punto fijo llamado vértice, el cual no pertenece al plano de la directriz.
El vértice o punta divide al cono en dos partes, llamadas hojas o ramas.
Ejercicios resueltos
– Ejercicio 1
Hallar el área lateral del cilindro circular recto de altura 25 cm, cuya curva directriz es la circunferencia de radio 6 cm, centrada en el origen.
Solución
El área lateral del cilindro es el producto de la longitud de la circunferencia directriz por la altura. Si R es el radio de la circunferencia y h es la altura del cilindro, el área viene dada por:
A = 2πR x h = 2πx 6 cm x 25 cm = 942.5 cm2
– Ejercicio 2
Se tiene la siguiente ecuación que corresponde a una superficie cuádrica:
x2 + y2 + 2z2 +2xz – 2yz = 1
Indicar de qué superficie se trata y cuál es la ecuación de la curva directriz.
Solución
Haciendo z = k, donde k es constante, se obtiene:
x2 + y2 + 2k2 +2kx – 2ky = 1
Reordenamos los términos de la siguiente manera:
(x2 + 2kx) + (y2– 2ky) = 1- 2k2
Hay que completar cuadrados en cada uno de los paréntesis de la izquierda, para ello se suma y se resta k2, para no alterar ninguno de los paréntesis:
(x2 + 2kx + k2 – k2 ) + (y2 – 2ky + k2 – k2) = 1- 2k2
(x2 + 2kx + k2) – k2 + (y2– 2ky + k2) – k2 = 1- 2k2
De esta forma queda:
(x + k)2 + (y – k)2 = 1
Como es la ecuación de una circunferencia de centro (-k, k) y radio 1, la superficie es un cilindro circular recto, también de radio 1, siempre y cuando la recta generatriz sea perpendicular a dicha circunferencia.
Por ejemplo, haciendo k = 0, la ecuación se reduce a la circunferencia centrada en el origen (0,0) cuyo radio es 1:
x2 + y2 = 1
Referencias
- Gaussianos. Representar superficies en tres dimensiones. Recuperado de: gaussianos.com.
- Kindle, J. Teoría y problemas de geometría analítica. McGraw Hill. Serie Schaum.
- Las superficies como lugares geométricos. Recuperado de:algebra.frlp.utn.edu.ar.
- Suárez, M. Superficies. Recuperado de: materias.unq.edu.ar.
- Superficies cuádricas. Recuperado de: sistemas.fciencias.unam.mx.
