Ley de Fick: primera, segunda, ejercicios
¿Qué es la ley de Fick?
La ley de Fick es una ecuación matemática que relaciona el flujo másico difundido en un medio con el gradiente de concentraciones o presiones. Fue formulada en 1855 por el fisiólogo y médico alemán Adolf Fick, quien inspirado por las leyes de Fourier (conducción térmica) y de Ohm (conducción eléctrica), modeló el proceso de difusión del oxígeno hacia los alvéolos de los pulmones.
La ley de Fick presenta la particularidad de que no es solamente aplicable a fenómenos de difusión químicos o bioquímicos, sino a los de cualquier tipo de naturaleza. Por lo tanto, sirve para modelar la difusión de átomos entre sólidos, siendo de mucha utilidad en la física de los materiales e ingeniería.
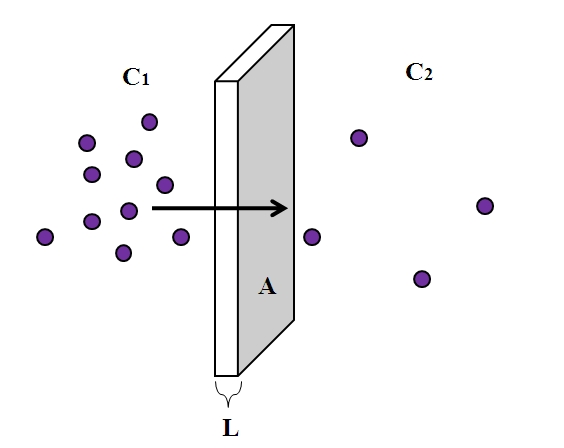
No obstante, la base central es la misma para casi todos los fenómenos de difusión, la cual está ilustrada arriba. Unas partículas moradas, séanse átomos o moléculas, se difunden a través de una membrana semipermeable de grosor L y área transversal A. A la izquierda tenemos una mayor concentración C1 de partículas que en la derecha, C2.
La ley de Fick establece lo siguiente: el flujo másico que se difunde a través de una superficie es proporcional al gradiente de concentración (C2-C1/L) y a una constante D llamada coeficiente de difusión o difusividad.
Esta ley posee dos formas: una en función del espacio (x), y otra en función del espacio y tiempo (x, t). La primera aplica para sistemas en condiciones estacionarias, mientras que la segunda para sistemas reales, no estacionarios.
Primera ley de Fick
Componentes y ecuación
El grosor L de la membrana semipermeable representa la distancia (x) que las partículas deben recorrer para llegar hacia el otro lado. Tal como se aprecia en la imagen, las partículas moradas mientras más se alejan del compartimiento izquierdo, donde C1 es grande, su concentración disminuye hasta el valor de C2. Es decir, la concentración cambia a lo largo del grosor de la membrana, siendo dependiente de x.
Esta variación de concentración en función de la distancia es lo que se conoce como gradiente de concentración: (C2-C1)/L o (C2-C1)/x. Nótese que su valor es negativo (-1), debido a que C2 > C1.
Por otro lado, tenemos también la velocidad con que las partículas se difunden a través de la membrana o del espacio en cuestión. Esta velocidad depende del tamaño y masa de las partículas, así como de la naturaleza del medio y la temperatura. El coeficiente de difusión D representa dicha velocidad, y puede ser constante o no durante la difusión.
Y por último, tenemos un flujo másico ‘j’ que atraviesa el área transversal de la membrana o del canal por donde se difunden las partículas. Agrupando estos términos nace la ecuación de la primera ley de Fick:
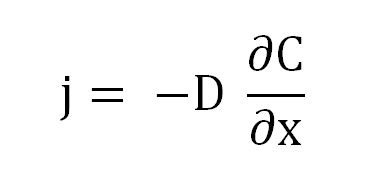
Donde j es proporcional a D y a (∂C/∂x), el gradiente de concentración.
Interpretación y unidades
El símbolo negativo en la ecuación sirve para neutralizar el signo negativo del gradiente de concentraciones. De lo contrario, j tendría un valor negativo, lo cual carece de sentido físico. Asimismo, el valor de D es positivo, para que al multiplicarse por el signo negativo que le antecede dé un valor negativo.
La primera ley de Fick señala lo siguiente: mientras mayor sea el gradiente de concentración (∂C/∂x), mayor será el flujo másico j. Es decir, la diferencia entre C2 y C1 se hace más grande y, por lo tanto, más partículas se difundirán a través de la membrana.
Por otro lado, j también depende de D, que a su vez es dependiente de parámetros como la temperatura, la viscosidad, el peso molecular, y el área transversal A:
D ∝ (A/L) (S/√MW)
Donde S es la solubilidad de la partícula que se difunde con el medio, y MW su peso molecular.
Respecto a las unidades de los componentes o términos de la ecuación tenemos:
-C (kg·m-3 o mol·m-3)
-D (m-2·s-1)
-j (kg·m-2·s-1 o mol·m-2·s-1)
Desplazamiento neto cuadrático medio
Durante la difusión las partículas colisionan unas con otras, y al cabo de cortos intervalos de tiempo terminan recorriendo enormes distancias Δx. Sin embargo, dependiendo del sentido de dichos desplazamientos, Δx puede tener valores negativos o positivos (de acuerdo a un punto de origen). Es por eso que el promedio de los valores de Δx para todas las moléculas tiende a 0.
Por otro lado, los valores de Δx son muy pequeños en comparación a las distancias que recorren las partículas. Cuando colisionan, pierden movilidad hacia una dirección, teniendo en consecuencia un desplazamiento neto limitado; por ejemplo, avanzan 2 cm en una dirección después de recorrer cientos de metros en colisiones y rebotes.
Einstein en 1905 encontró una expresión matemática para el promedio del cuadrado del desplazamiento (por ende distinto a 0):
(Δx)2> = 2Dt
Definiendo
(Δx)rms ≡ (Δx)2>1/2 = (2Dt)1/2
(Δx)rms es el desplazamiento neto cuadrático medio de las partículas en cuestión. (Δx)rms nos dice cuánto se desplaza en promedio unas partículas (en dirección positiva o negativa) de acuerdo al tiempo. Algunas partículas se desplazarán distancias más lejanas o cercanas que (Δx)rms, originando una distribución gaussiana.
Segunda ley de Fick
Ecuación
La primera ley de Fick describe la difusión en condiciones estacionarias, es decir, el flujo másico j no varía con el tiempo. En sistemas reales, sin embargo, tenemos condiciones no estacionarias, donde el flujo másico no solo varía en el espacio, sino también con el tiempo. Por lo tanto, interesa determinar (∂C/∂t).
Abajo tenemos dos ecuaciones que representan la segunda ley de Fick:
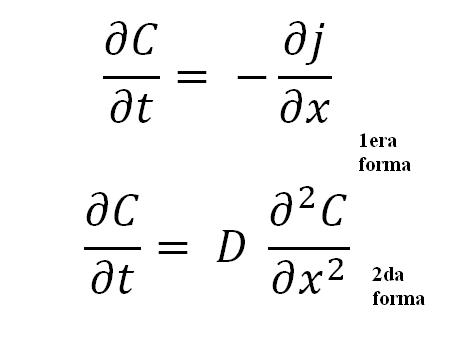
La 2da forma es la más importante de todas, pues representa la ecuación matemática general para cualquier proceso de difusión; ya sea térmica, eléctrica, atómica, etc.
Deducción
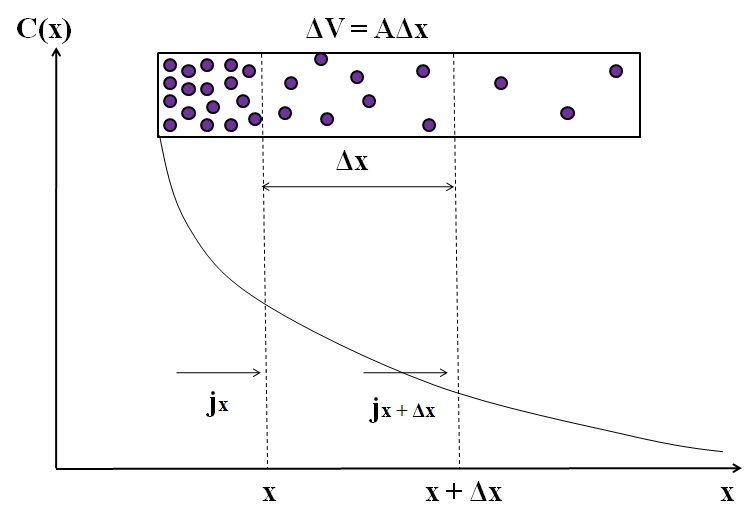
Considérese otra vez las partículas moradas en una cámara rectangular. Entre las distancias x y x+Δx tenemos un flujo jx (entrante) y jx+Δx (saliente). El volumen de la cámara entre esas distancias viene definido por:
ΔV = AΔX
Nótese que la gráfica C(x) vs x no origina una línea recta, por lo que tenemos diferentes valores de j (jx ≠ jx+Δx). Debemos determinar ΔC/Δt.
La masa mx será igual a:
mx = jx AΔt
Un análisis dimensional ayuda a comprender por qué:
kg = (kg·m-2·s-1) (m2) (s)
Del mismo modo calculamos mx+Δx:
mx+ Δx = jx+Δx AΔt
Siendo la masa que se acumula en dicha región igual a Δm:
Δm = mx – mx+ Δx
= (jx – jx+ Δx) AΔt
= -(jx+ Δx – jx) AΔt
= -ΔjAΔt
Y sabiendo que ΔC= Δm/ΔV
ΔC= -ΔjAΔt/ ΔV
= -ΔjAΔt /AΔx
=-ΔjΔt/Δx
Despejamos ΔC/Δt
ΔC/Δt = -Δj/Δx
Esta expresión nos indica que la variación de la concentración en el tiempo es igual a la variación del flujo j con respecto a su desplazamiento. Aplicando los límites para Δt y Δx tendiendo a 0 obtenemos la misma expresión como una derivada parcial:
∂C/∂t = -(∂j/∂x) (1era forma)
Finalmente, la 2da forma se obtiene sustituyendo j con la primera ley de Fick:
∂C/∂t = -∂/∂x(-D∂C/∂x)
= D(∂2C/∂x2) (2da forma)
Ejercicios resueltos
En los ejercicios siguientes se considerarán sistemas muy simples cuyas incógnitas pueden resolverse utilizando la primera ley de Fick.
Ejercicio 1
Enunciado
En una tubería de 15 metros de largo y 21 centímetros de ancho, y que además está saturada de nitrógeno, se difunde una corriente de oxígeno de un extremo a otro a una temperatura de 0 ºC. Sabiendo que la presión en el lado izquierdo (P1) es 20 kg/m3, y que la presión en el lado derecho (P2) es 10 kg, determine:
a) el flujo másico que se difunde
b) ¿cuántos kilogramos de O2 se difundirán por la tubería en 17 minutos?
c) el gradiente de concentración o presiones
d) la presión del O2 a una distancia de 7 metros de la entrada a la tubería
e) ¿cuánto demorará 80 kg de O2 en difundirse por esta tubería?
Considere que DO2-N2 es igual a 1.8·10-5 m2·s-1.
Resolución
De la primera ley de Fick tenemos para resolver el inciso a):
j = -D(P2-P1)/L
= -(1.8·10-5 m2·s-1)(10-20)(kg/m3)/(15m)
=1.2·10-5 kg·m-2·s-1
Para b) necesitamos el área de la tubería:
A = π(0.21 m)2
=0.14 m2
Y multiplicamos j por A y el tiempo t para determinar la masa de O2 difundida:
mO2 = (1.2·10-5 kg·m-2·s-1)(17 s)(0.14 m2)
=3.57·10-5 kg
Ahora, para el inciso c) tenemos que el gradiente es igual a:
Gradiente= (P2-P1)/L
= (10-20)(kg/m3)/15 m
= -2/3 (kg/m3)·m-1
Pero tomamos el valor positivo, que tiene sentido físico:
2/3 (kg/m3)·m-1
Este valor nos servirá entonces para resolver el inciso d) si se interpreta bien el gradiente: cada metro la presión de O2 caerá 2/3 kg/m3. Al difundirse 7 metros tendremos pues:
2/3 (kg/m3)·m-1 (7 m) = 14/3 o 4.7 kg/m3
Es decir, que la presión a esa distancia será:
(20-4.7)(kg/m3) = 15.3 kg/m3
Y finalmente, el inciso e) es parecido al b), solamente que ahora despejamos el tiempo y no la masa:
mO2 = jAt
t = mO2/jA
= (80 kg)/(1.2·10-5 kg·m-2·s-1)(0.14 m2)
=47619.04 s o 0.55 día
Ejercicio 2
Enunciado
Determine (Δx)rms para la sacarosa en agua a t = 1 min, 1 h y 1 día. El coeficiente de difusión de la sacarosa en agua es 0.52·10-5cm2·s-1.
Resolución
Aplicamos la ecuación:
(Δx)rms ≡ (Δx)2>1/2 = (2Dt)1/2
Evaluamos (Δx)rms con los tiempos expresados en segundos. Para t =1 min o 60 s:
(Δx)rms = ((2(0.52·10-5cm2·s-1)(60s))1/2
= 0.025 cm
Para t= 1 h o 3600 s:
(Δx)rms = ((2(0.52·10-5cm2·s-1)(3600s))1/2
= 0.19 cm
Y finalmente para t= 1 día o 86400 s:
(Δx)rms = ((2(0.52·10-5cm2·s-1)(86400s))1/2
= 0.95 cm
Nótese que conforme transcurre el tiempo las moléculas de sacarosa ni siquiera han podido desplazarse 1 cm en ninguna de las direcciones.
Referencias
- Walter J. Moore. (1963). Physical Chemistry. In Chemical kinetics. Fourth edition, Longmans.
- Ira N. Levine. (2009). Principios de fisicoquímica. Sexta edición. Mc Graw Hill.
- Introduction to Materials Science and Engineering. (11 de marzo de 2018). Fick’s second law. Prof. Rajesh Prasad. [VIDEO]. Recuperado de: youtube.com
- Wikipedia. (2020). Fick’s laws of diffusion. Recuperado de: en.wikipedia.org
- Laura Dickson. (10 de septiembre de 2020). Diffusion. Chemistry LibreTexts. Recuperado de: chem.libretexts.org
- Larissa Zhou et al. (01 de septiembre de 2015). Understanding diffusion theory and Fick’s law through food and cooking. The American Physiological Society. doi.org/10.1152/advan.00133.2014
