Volumen específico: qué es, fórmula, unidades, cálculo, ejemplos

¿Qué es el volumen específico?

El volumen específico (representado con el símbolo ν, letra griega nu) es una propiedad intensiva de la materia que mide el volumen ocupado por unidad de masa de un cuerpo. Corresponde a la relación entre el volumen y la masa, por lo que representa el inverso de la densidad. Esto quiere decir que, mientras más denso sea un cuerpo, menor será su volumen específico y viceversa.

Conocer el volumen específico de una sustancia es importante en aplicaciones en las que el volumen disponible sea limitado. Por ejemplo, al seleccionar el combustible para un cohete espacial, lo ideal es que el combustible tenga el menor volumen específico posible, ya que de lo contrario ocupará demasiado espacio lo que requerirá un cohete muy grande y costoso.

Los volúmenes específicos también son de gran importancia en el campo de la termodinámica, ya que permiten calcular de manera sencilla los volúmenes molares de distintas sustancias a partir de su masa molar, o para determinar el volumen total de una muestra a partir de su masa.

Finalmente, los cambios de volumen específico también permiten caracterizar cambios de fase como la fusión y la ebullición, entre otros.

Fórmula del volumen específico

La siguiente ecuación corresponde a la definición matemática del volumen específico:

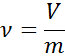
donde V es el volumen de un cuerpo o de una sustancia, m es su masa y ν es el volumen específico. Sin embargo, también se puede calcular a partir de la densidad, ya que, como se mencionó anteriormente, el volumen específico es el inverso de la densidad:

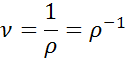
donde ρ representa la densidad.

Unidades del volumen específico

Las unidades del volumen específico son unidades de volumen sobre unidades de masa. Como de costumbre, estas magnitudes se pueden expresar en diferentes sistemas de unidades, por lo que el volumen específico también se puede expresar en distintas unidades.

En la siguiente tabla se muestran las unidades del volumen específico en los sistemas de unidades de mayor importancia:

Cálculo del volumen específico

Para sólidos regulares

En el caso de los sólidos regulares, la manera más sencilla de determinar el volumen específico es determinando el volumen a partir de las dimensiones del sólido, y luego dividiendo entre la masa.

Para determinar el volumen del sólido se emplea la fórmula de volumen correspondiente a la forma particular que tenga el sólido (esfera, cono, cilindro, etc.).

Ejemplo 1: Barra cilíndrica

Se tiene una barra cilíndrica sólida de 2,54 cm de grosor, 10 cm de largo y una masa de 1,50 kg. Determine el volumen específico del material en unidades del S.I.

• Solución: como sabemos que se trata de un cilindro, entonces debemos utilizar la fórmula de volumen de un cilindro para luego aplicar la fórmula de volumen específico. Ambas ecuaciones se pueden combinar en una sola como se muestra a continuación:

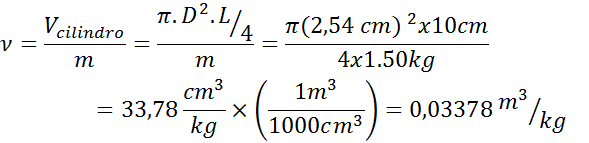
Ejemplo 2: Esfera de vidrio

Una canica de vidrio de 1 cm de diámetro se pesa en una balanza. Esta lee 2,50 g. Determine el volumen específico del vidrio.

• Solución: a partir del diámetro se sabe que el radio de la esfera es de 0,50 cm. Con este radio y utilizando la fórmula de volumen de una esfera podemos determinar el volumen de la canica. Luego, utilizamos la fórmula del volumen específico. También se pueden combinar ambas ecuaciones en una sola:

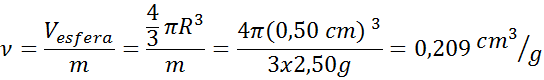
Para sólidos amorfos

En el caso de los sólidos amorfos no es posible determinar su volumen por medio de fórmulas, ya que no se trata de sólidos regulares. Una posible solución es determinar el volumen del cuerpo por medio del volumen que desplaza al sumergirse en agua o en otro líquido:

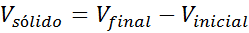
Ejemplo 3: Un meteorito

Se encontró un meteorito de forma muy extraña. Primero se pesó, tras lo cual se obtuvo una masa de 185,3 g. Luego se introdujo en un cilindro graduado que contenía 50,0 mL de agua. Luego de sumergido el meteorito, el nivel del agua aumentó hasta 73,5 mL. Determine el volumen específico del meteorito.

• Solución: como se mencionó anteriormente, el volumen del meteorito se determina por el desplazamiento de líquido. La diferencia entre los volúmenes de agua en el cilindro graduado antes y después de sumergir el meteorito da el volumen del mismo. Luego, se aplica la fórmula de volumen específico:

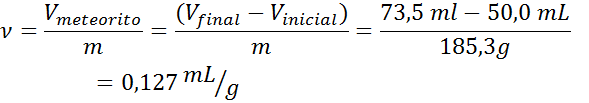
Ejemplo 4: Una roca

Cerca del sitio en el que se encontró el meteorito del ejemplo anterior, se encontró otra roca con apariencia similar. Esta también se pesó, obteniéndose una masa de 125 g y se sumergió en agua, donde desplazó 15,90 mL del líquido. Determine si se trata o no de un fragmento de meteorito.

• Solución: el volumen específico es una propiedad intensiva, así que si la roca está hecha del mismo material que el meteorito, debería  tener el mismo volumen específico.

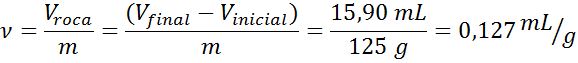
Como se puede ver, el volumen específico de la roca es idéntico al del meteorito, por lo que es posible que la roca sea un fragmento del mismo.

Para líquidos

Calcular el volumen específico de un líquido se hace de la misma manera como se ha mostrado en los ejemplos anteriores. El volumen se puede medir fácilmente utilizando material volumétrico. También se puede calcular el volumen específico a partir de la densidad del líquido, como se muestra en el siguiente ejemplo.

Ejemplo 5: Volumen específico del alcohol desnaturalizado

Determine el volumen específico del alcohol desnaturalizado, sabiendo que tiene una densidad de 0,876 g/mL.

• Solución: sabemos que el volumen específico es el inverso de la densidad, así que:

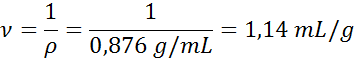
Para gases

En vista de que la mayoría de los gases cumplen relativamente bien la ley de los gases ideales, entonces esta ecuación puede utilizarse para determinar el valor del volumen específico de un gas. Luego de reordenar esta ecuación se obtiene la siguiente relación:

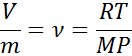
donde R, T, M y P son la constante de los gases ideales, la temperatura, la masa molar del gas y la presión, respectivamente.

Ejemplo 6: Volumen específico del aire

Calcule el volumen específico de una muestra de aire que se encuentra a 2 atm de presión y a 350 °C, sabiendo que la masa molar promedio del aire es de 28,96 g/mol.

• Solución: para utilizar esta ecuación es necesario primero transformar la temperatura a Kelvin sumando 273 a la temperatura en grados Celsius: T=350+273 = 623 K. Ahora podemos aplicar la ecuación anterior, utilizando el valor de la constante R = 0,08206 atl.L/mol.K: