Compresibilidad: de sólidos, de líquidos, de gases, ejemplos
La compresibilidad de una sustancia o material es el cambio de volumen que experimenta cuando es sometida a un cambio de presión. Por lo general el volumen disminuye al aplicar una presión sobre un sistema u objeto. Sin embargo, en ocasiones ocurre lo contrario: un cambio en la presión puede producir una explosión en la cual el sistema aumenta el volumen, o bien cuando tiene lugar un cambio de fase.
En algunas reacciones químicas puede suceder esto y en los gases también, ya que al aumentar la frecuencia de las colisiones, las fuerzas repulsivas van tomando lugar.

Al imaginar cómo de fácil o difícil puede ser comprimir un objeto, hay que considerar los tres estados en que normalmente está la materia: sólido, líquido y gaseoso. En cada uno de ellos las moléculas guardan ciertas distancias entre sí. Cuanto más firmes los enlaces que unen las moléculas de la sustancia que compone al objeto y más cercanas se encuentren, más difícil será causarle una deformación.
Un sólido tiene sus moléculas muy cercanas, y al intentar juntarlas más, aparecen fuerzas de repulsión que dificultan la tarea. Por ello se dice que los sólidos son poco compresibles. En las moléculas de los líquidos hay más espacio, así que su compresibilidad es mayor, pero aun así el cambio de volumen suele requerir de fuerzas grandes.
Así que los sólidos y los líquidos son difícilmente compresibles. Haría falta una variación de presión muy grande para lograr un cambio de volumen apreciable en las llamadas condiciones normales de presión y temperatura. En cambio los gases, como tienen las moléculas muy espaciadas, se comprimen y descomprimen fácilmente.
Índice del artículo
- 1 Compresibilidad de sólidos
- 2 Ejercicios resueltos-ejemplos
- 3 Compresibilidad en los gases
- 4 Referencias
Cuando se sumerge un objeto en un fluido por ejemplo, este ejerce presión sobre el objeto en todas las direcciones. De esta manera podemos pensar que el volumen del objeto disminuirá, aunque en la mayor parte de los casos esto no será apreciable.
La situación se aprecia en la siguiente figura:
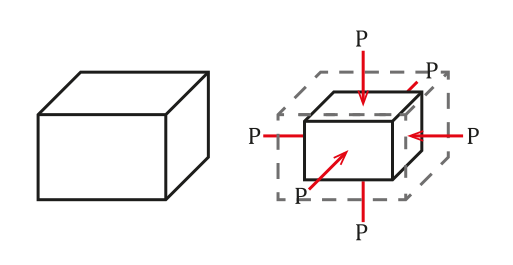
La presión se define como fuerza por unidad de área, la cual ocasionará un cambio de volumen ΔV proporcional al volumen inicial del objeto Vo. Este cambio de volumen dependerá de las cualidades del mismo.
La ley de Hooke afirma que la deformación experimentada por un objeto es proporcional al esfuerzo aplicado sobre él:
Esfuerzo ∝ Deformación
La deformación volumétrica experimentada por un cuerpo se cuantifica por B la constante de proporcionalidad requerida, la cual es denominada como el módulo volumétrico del material:
B= -Esfuerzo/Deformación unitaria
B = -ΔP/ (ΔV/Vo)
Como ΔV/Vo es una cantidad adimensional, por ser el cociente entre dos volúmenes, el módulo volumétrico tiene las mismas unidades de la presión, que en Sistema Internacional son Pascales (Pa).
El signo negativo indica la esperada reducción en el volumen, cuando al objeto se lo comprime lo suficiente, es decir, la presión aumenta.
Al valor inverso o recíproco del módulo volumétrico se le conoce como compresibilidad y se denota con la letra k. Por lo tanto:
Aquí k es el negativo del cambio fraccional de volumen por incremento en la presión. Sus unidades en Sistema Internacional son las inversas del Pa, es decir m2 /N.
La ecuación para B o para k si se prefiere, es aplicable tanto a sólidos como a líquidos. El concepto de módulo volumétrico rara vez se aplica a los gases. Más adelante se explica un modelo sencillo para cuantificar la disminución de volumen que puede experimentar un gas real.
La velocidad del sonido y el módulo de compresibilidad
Una aplicación interesante es la velocidad del sonido en un medio, la cual depende del módulo de compresibilidad del mismo:
Una esfera de latón macizo cuyo volumen es 0.8 m3 se deja caer en el océano hasta una profundidad en la cual la presión hidrostática es 20 M Pa mayor que en la superficie. ¿Qué cambio experimentará el volumen de la esfera? Se sabe que el módulo de compresibilidad del latón es B = 35 000 MPa,
Solución
1 M Pa = 1 Mega pascal = 1. 10 6 Pa
La variación de presión con respecto a la superficie es DP = 20 x 10 6 Pa. Aplicando la ecuación dada para B, se tiene:
B = -ΔP/ (ΔV/Vo)
Por lo tanto:
ΔV = -5.71.10 -4 x 0.8 m3 = -4.57 x 10-4 m3
La diferencia de volumen puede tener signo negativo cuando el volumen final es menor que el volumen inicial, por lo tanto este resultado está de acuerdo con todas las suposiciones que hemos hecho hasta ahora.
El módulo de compresibilidad tan alto, indica que se requiere un gran cambio en la presión para que el objeto experimente una disminución de volumen apreciable.
Poniendo el oído contra las vías del tren se sabe cuando se aproxima uno de estos vehículos en la lejanía. ¿Cuánto tarda el sonido al viajar por un riel de acero si el tren está a 1 km de distancia?
Datos
Densidad del acero = 7.8 x 10 3 kg/m3
Módulo de compresibilidad del acero = 2.0 x 10 11 Pa.
Solución
El módulo de compresibilidad B calculado anteriormente se aplica también a los líquidos, aunque por lo general se requiere un gran esfuerzo para producir una disminución apreciable de volumen. Pero los fluidos pueden expandirse o contraerse según se calienten o se enfríen, e igualmente si se despresurizan o presurizan.
Para el agua en condiciones estándar de presión y temperatura (0 ºC y una atmósfera de presión aproximadamente o 100 kPa), el módulo volumétrico es 2100 MPa. Es decir, unas 21000 veces la presión atmosférica.
Por ello en la mayoría de las aplicaciones los líquidos suelen considerarse incompresibles. Esto se puede comprobar de inmediato con aplicación numérica.
Encontrar el decremento fraccional del volumen del agua cuando está sometida a una presión de 15 MPa.
Solución
Los gases, tal como se explicó anteriormente, funcionan de manera un poco diferente.
Para saber qué volumen tienen n moles de un gas dado cuando se lo mantiene confinado a una presión P y a una temperatura T, se utiliza la ecuación de estado. En la ecuación de estado para un gas ideal, donde las fuerzas intermoleculares no se toman en cuenta, el modelo más sencillo señala que:
P.Videal = n. R. T
Donde R es la constante de los gases ideales.
Los cambios en el volumen del gas pueden llevarse a cabo a presión constante o a temperatura constante. Por ejemplo, al mantener constante la temperatura, la compresibilidad isotérmica ΚT es:
En vez del símbolo “delta” que se utilizó antes al definir el concepto para los sólidos, para un gas se describe con derivada, en este caso derivada parcial respecto a P, manteniendo T constante.
Por lo tanto BT el módulo de compresibilidad isotérmico es:
Y también es importante el módulo de compresibilidad adiabático Badiabático, para el cual no hay flujo de calor entrante o saliente.
Badiabático = γp
Donde γ es el coeficiente adiabático. Con este coeficiente se puede calcular la velocidad del sonido en el aire:
Aplicando la ecuación anterior, encuentre la velocidad del sonido en el aire.
Datos
El módulo de compresibilidad adiabático del aire es 1,42×105 Pa
La densidad del aire es 1.225 kg/m3 (a presión atmosférica y 15 ºC)
Solución
En vez de trabajar con el módulo de compresibilidad, como cambio unitario de volumen por cambio de presión, puede ser interesante el factor de compresibilidad de un gas real, un concepto diferente pero ilustrativo acerca de cómo se compara el gas real con el gas ideal:
P . Vreal = Z. R. T
Donde Z es el coeficiente de compresibilidad del gas, el cual depende de las condiciones en que este se encuentre, siendo por lo general una función tanto de la presión P como de la temperatura T, pudiendo expresarse como:
Z = f (P,T)
En el caso de un gas ideal Z = 1. Para los gases reales el valor Z casi siempre aumenta con la presión y disminuye con la temperatura.
Al aumentar la presión las moléculas gaseosas colisionan con más frecuencia y se incrementan las fuerzas repulsivas entre ellas. Esto puede dar lugar a un aumento de volumen en el gas real, por lo cual Z > 1.
En cambio, a presiones más bajas, las moléculas tienen libertad de moverse y predominan las fuerzas de atracción. En tal caso, Z 1.
Para el caso sencillo de 1 mol de gas n = 1, si se mantienen las mismas condiciones de presión y temperatura, al dividir término a término las ecuaciones anteriores se obtiene:
Vreal = Z Videal
Se tiene un gas real a 250 ºK y 15 atm de presión, el cual posee un volumen molar un 12 % menor que el calculado mediante la ecuación de estado de los gases ideales. Si la presión y la temperatura se mantienen constantes, encontrar:
a) El factor de compresibilidad.
b) El volumen molar del gas real.
c) ¿Qué tipo de fuerzas predominan: atractivas o repulsivas?
Solución
a) Si el volumen real es 12 % menor que el ideal, significa que:
Vreal = 0.88 Videal
Por lo tanto para 1 mol de gas, el factor de compresibilidad es:
Z = 0.88
b) Escogiendo la constante de los gases ideales con las unidades apropiadas para los datos suministrados:
R = 0,082 L.atm/mol.K
El volumen molar se calcula despejando y sustituyendo valores:
c) Predominan las fuerzas atractivas, ya que Z es menor que 1.
- Atkins, P. 2008. Química Física. Editorial Médica Panamericana. 10 – 15.
- Giancoli, D. 2006. Physics: Principles with Applications. 6th. Ed Prentice Hall. 242 – 243 y 314-15
- Mott, R. 2006. Mecánica de Fluidos. Pearson Educación.13-14.
- Rex, A. 2011. Fundamentos de Física. Pearson Educación. 242-243.
- Tipler, P. (2006) Física para la Ciencia y la Tecnología. 5ta Ed. Volumen 1. Editorial Reverté. 542.
