Constante de Boltzmann: historia, ecuaciones, cálculo, ejercicios
La constante de Boltzmann es el valor que relaciona la energía cinética media de un sistema termodinámico o un objeto con la temperatura absoluta del mismo. Aunque con frecuencia se confunden, la temperatura y la energía no son un mismo concepto.
La temperatura es una medida de la energía, pero no la energía en sí. Con la constante de Boltzmann se vincula la una a la otra de la siguiente forma:
Ec = (3/2) kB T

Esta ecuación es válida para una molécula de gas ideal monoatómico de masa m, donde Ec es su energía cinética dada en Joules, kB es la constante de Boltzmann y T es la temperatura absoluta en Kelvin.
De esta manera, cuando la temperatura aumenta, la energía cinética promedio por molécula de sustancia también aumenta, tal como se espera que suceda. Y lo contrario pasa cuando la temperatura disminuye, pudiéndose llegar al punto en que si todo el movimiento cesa, se alcanza la temperatura más baja posible o cero absoluto.
Al hablar de energía cinética promedio es necesario recordar que la energía cinética está asociada al movimiento. Y las partículas pueden moverse de muchas formas, por ejemplo trasladándose, rotando o vibrando. Claro que no todas lo harán de la misma forma, y como son incontables, entonces se toma el promedio para caracterizar el sistema.
Algunos estados de energía son más probables que otros. Este concepto es de radical importancia en la termodinámica. La energía considerada en la ecuación anterior es energía cinética de traslación. De la probabilidad de los estados y su relación con la constante de Boltzmann se hablará un poco más adelante.
En 2018 se redefinió el Kelvin y con él la constante de Boltzmann, que en el Sistema Internacional es aproximadamente 1.380649 x 10-23 J. K-1. Se puede lograr mucha más precisión para la constante de Boltzmann, la cual ha sido determinada en numerosos laboratorios alrededor del mundo, por diferentes métodos.
Índice del artículo
- 1 Historia
- 2 Valor y ecuaciones
- 3 La constante de Boltzmann y la entropía
- 4 ¿Cómo se calcula kB?
- 5 Ejercicios resueltos
- 6 Referencias
La famosa constante debe su nombre al físico Ludwig Boltzmann (1844–1906), nacido en Viena, quien dedicó su vida como científico al estudio del comportamiento estadístico de los sistemas con muchas partículas, desde el punto de vista de la mecánica newtoniana.
Aunque hoy en día la existencia del átomo es aceptada universalmente, en el siglo XIX estaba en pleno debate la creencia sobre si el átomo existía realmente o era un artificio con el cual se explicaban muchos fenómenos físicos.
Boltzmann era un férreo defensor de la existencia del átomo, y en su tiempo enfrentó duras críticas a sus trabajos por parte de muchos colegas, quienes consideraron que estos contenían paradojas insolubles.
Él declaró que los fenómenos observables a niveles macroscópicos podían ser explicados mediante las propiedades estadísticas de las partículas constituyentes como átomos y moléculas.
Puede que a estas críticas se debiera el profundo episodio de depresión que le llevó a quitarse la vida a comienzos de septiembre de 1906, cuando todavía tenía mucho por hacer, pues era considerado uno de los grandes físicos teóricos de su tiempo y faltaba muy poco para que otros científicos contribuyeran a corroborar la veracidad de sus teorías.
No pasó mucho tiempo después de su muerte cuando nuevos descubrimientos acerca de la naturaleza del átomo y sus partículas constituyentes se sumaran para darle la razón a Boltzmann.
Ahora bien, la constante de Boltzmann kB fue introducida tal como se la conoce hoy en día un tiempo después de los trabajos del físico austríaco. Fue Max Planck, en su ley de la emisión del cuerpo negro, un trabajo que presentó en 1901, quien en aquel momento le dio el valor de 1,34 x 10−23 J/K.
Hacia el año 1933 se le agregó a la lápida de Boltzmann en Viena a modo de homenaje póstumo una placa con la definición de la entropía que involucra la famosa constante: S = kB log W, ecuación de la cual se hablará más adelante.
Hoy en día la constante de Boltzmann es indispensable en la aplicación de las leyes de termodinámica, la mecánica estadística y la teoría de la información, campos de los cuales este físico con triste final fue pionero.
Los gases se pueden describir en términos macroscópicos y también en términos microscópicos. Para la descripción primera existen conceptos como la densidad, la temperatura y la presión.
Sin embargo, conviene recordar que un gas está compuesto de muchas partículas, las cuales poseen una tendencia global a un cierto comportamiento. Es esa tendencia la que se mide macroscópicamente. Una forma de determinar la constante de Boltzmann es gracias a la conocida ecuación de los gases ideales:
p.V= n. R. T
Aquí p es la presión del gas, V es su volumen, n es el número de moles presentes, R es la constante de los gases y T es la temperatura. En un mol de gas ideal se cumple la siguiente relación entre el producto p.V, y la energía cinética de traslación K del todo el conjunto es:
p.V = (2/3). K
Por lo tanto la energía cinética es:
K = (3/2) n.R.T
Al dividir entre el número total de moléculas presentes, al cual se llamará N, se obtiene la energía cinética promedio de una sola partícula:
Ec = K /N
Ec= (3/2N) n.R.T
En un mol hay el número de Avogadro de partículas NA, y por lo tanto el número total de partículas es N = nNA, quedando:
Ec = (3/2nNA) n.R.T
Precisamente el cociente R/NA es la constante de Boltzmann, quedando demostrado así que la energía cinética de traslación promedio de una partícula depende solamente de la temperatura absoluta T y no de otras magnitudes como presión, volumen o siquiera el tipo de molécula:
Ec = (3/2) kB. T
Un gas tiene una temperatura dada, pero esa temperatura puede corresponder a distintos estados de energía interna. ¿Cómo visualizar esta diferencia?
Considérese el lanzamiento simultáneo de 4 monedas y las formas en que éstas pueden caer:
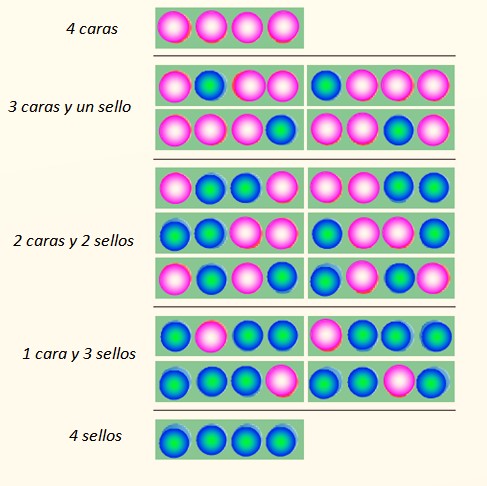
El conjunto de monedas puede asumir un total de 5 estados, los cuales son considerados macroscópicos, descritos en la figura. ¿Cuál de estos estados diría el lector que es el más probable?
La respuesta debería ser el estado de 2 caras y 2 cruces, porque tiene un total 6 posibilidades, de las 16 ilustradas en la figura. Y 24 = 16. Estos equivalen a los estados microscópicos.
¿Y qué tal si se lanzan 20 monedas en vez de 4? Habría un total de 220 posibilidades o “estados microscópicos”. Es un número bastante mayor y más difícil de manejar. Para facilitar el manejo de números grandes, los logaritmos son muy apropiados.
Ahora bien, lo que sí parece evidente es que el estado con mayor desorden es el más probable. Los estados más ordenados como 4 caras o 4 sellos son un poco menos probables.
Se define la entropía de un estado macroscópico S como:
S = kB ln w
Donde w es el número de estados microscópicos posibles del sistema y kB es la constante de Boltzmann. Como ln w es adimensional, la entropía tiene las mismas unidades que kB: Joule/K.
Esta es la famosa ecuación en la lápida de Boltzmann en Viena. Sin embargo, más que la entropía, lo relevante es el cambio de ella:
ΔS = kB ln w2 – kB ln w1 = kB ln (w2/w1)
El valor de la constante de Boltzmann se obtiene experimentalmente de forma sumamente precisa con mediciones basadas en termometría acústica, las cuales se llevan a cabo usando la propiedad que establece la dependencia de la velocidad del sonido en un gas con la temperatura del mismo.
En efecto, la velocidad del sonido en un gas está dada por:
Badiabático = γp
Y ρ es la densidad del gas. Para la ecuación anterior, p es la presión del gas en cuestión y γ es el coeficiente adiabático, cuyo valor para un gas determinado se encuentra en tablas.
Los institutos de metrología también experimentan otras formas de medir la constante, como por ejemplo la Johnson Noise Thermometry, que utiliza las fluctuaciones térmicas que se dan aleatoriamente en los materiales, en particular en los conductores.
Encuentre:
a) La energía cinética de traslación promedio Ecque tiene una molécula de gas ideal a 25 ºC
b) La energía cinética de traslación K de las moléculas en 1 mol de este gas
c) La rapidez promedio de una molécula de oxígeno a 25 ºC
Dato
moxigeno = 16 x 10 -3 kg/mol
Solución
a) Ec = (3/2) k T = 1.5 x 1.380649 x 10-23J. K-1 x 298 K = 6.2 x 10-21 J
b) K = (3/2) n.R.T= 5 x 1 mol x 8.314 J/mol .K x 298 K= 3716 J
c) Ec = ½ mv2, tomando en cuenta que la molécula de oxígeno es diatómica y hay que multiplicar la masa molar por 2, se tendrá:
Encuentre el cambio de entropía cuando 1 mol de gas que ocupa un volumen de 0.5 m3 se expande para ocupar 1 m3.
Solución
ΔS = kB ln (w2/w1)
w2= 2Nw1 (Había 24 estados microscópicos para el lanzamiento de las 4 monedas, ¿recuerda?)
Donde N es el número de partículas presentes en 0.5 mol de gas 0.5 x NA:
ΔS = kB ln (2N w1/w1)= kB ln 2N= kB 0.5NA ln 2 =2.88 J/K
- Atkins, P. 1999. Química Física. Ediciones Omega. 13-47.
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill. 664- 672.
- Giancoli, D. 2006. Physics: Principles with Applications. 6th.. Ed Prentice Hall. 443 -444.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1. 647-673.
- SI Redefinition. Kelvin: Boltzmann Constant. Recobrado de: nist.gov
