Coordenadas rectangulares: ejemplos y ejercicios resueltos
Las coordenadas rectangulares o cartesianas son aquellas que se obtienen al proyectar ortogonalmente sobre los tres ejes cartesianos X, Y, Z un punto ubicado en el espacio tridimensional.
Los ejes cartesianos son rectas orientadas mutuamente perpendiculares entre sí. En el sistema de coordenadas cartesiano, a cada punto del espacio se le asignan tres números reales que son sus coordenadas rectangulares.

Un plano es un subespacio del espacio tridimensional. En caso de considerar puntos sobre un plano, basta entonces con elegir un par de ejes perpendiculares X,Y como sistema cartesiano. Entonces a cada punto del plano se le asignan dos números reales que son sus coordenadas rectangulares.
Índice del artículo
- 1 Origen de coordenadas rectangulares
- 2 El plano cartesiano
- 3 Ejemplos
- 4 Ejercicios resueltos
- 5 Referencias
Las coordenadas rectangulares fueron propuestas originalmente por el matemático francés René Descartes (1596 y 1650), motivo por el cual reciben la denominación de cartesianas.
Con esta idea de Descartes, a los puntos del plano y del espacio se le asignan números, de modo que las figuras geométricas tienen asociadas una ecuación algebraica y los teoremas geométricos clásicos pueden ser demostrados algebraicamente. Con las coordenadas cartesianas nace la geometría analítica.
Si en un plano se eligen dos rectas perpendiculares que se intersecan en un punto O; y si además a cada recta se le asigna una dirección y una escala numérica entre puntos equidistantes sucesivos, se tiene entonces un sistema o plano cartesiano en el que cada punto del plano se asocia un par ordenado de dos números reales que son sus proyecciones respectivamente sobre los ejes X e Y.
Los puntos A=(3, 2); B=(-2, 3); C=(-2, -3) y D=(3, -3) se representan en el plano cartesiano como se muestra a continuación:
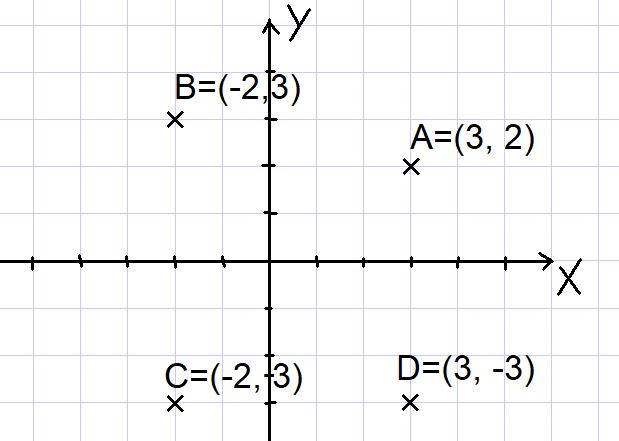
Nótese que los dos ejes X e Y dividen el plano en cuatro sectores denominados cuadrantes. El punto A está en el primer cuadrante, el B en el segundo cuadrante, el C en el tercer cuadrante y el punto D en el cuarto cuadrante.
La distancia entre dos puntos A y B del plano cartesiano es la longitud del segmento que los une. Dicha distancia puede calcularse analíticamente de la siguiente manera:
d(A, B)=√(Bx – Ax)^2 + (By – Ay)^2)
La fórmula anterior se obtiene mediante la aplicación del teorema de Pitágoras.
Aplicando dicha fórmula a los puntos A, B de la figura 2 se tiene:
d(A, B) = √(-2 – 3)^2 + (3 – 2)^2) = √(-5)^2 + 1^2) = √(26)
Es decir, que d(A, B)=5,10 unidades. Nótese que la distancia se obtuvo sin la necesidad de medir con una regla, se ha seguido un procedimiento completamente algebraico.
Las coordenadas rectangulares permite la representación analítica de objetos geométricos fundamentales como el punto y la recta. Dos puntos A y B definen una única recta. Se define la pendiente de la recta como el cociente entre la diferencia de las coordenadas Y del punto B menos el A, dividida entre la diferencia de las coordenadas X del punto B menos el A:
pendiente= (By – Ay)/(Bx – Ax)
Un punto cualquiera P de coordenadas (x, y) que pertenezca a la recta (AB) debe tener la misma pendiente:
pendiente= (y – Ay)/(x – Ax)
La ecuación que se obtiene mediante la igualdad de las pendientes es la representación analítica o algebraica de la recta que pasa por los puntos A y B:
(y – Ay)/(x – Ax) = (By – Ay)/(Bx – Ax).
Si se toma para A y B las coordenadas rectangulares de la figura 2 se tiene:
(y – 2)/(x – 3) = (3 – 2)/(-2 – 3)
(y – 2)/(x – 3) = -⅕
En este caso particular se tiene una recta con pendiente negativa -⅕, lo que significa que ubicándose sobre un punto de la recta e incrementando la coordenada x en una unidad, la coordenada y decrece en 0,2 unidades.
La forma más usual de escribir la ecuación de la recta en el plano es con la coordenada y despejada como función de la variable x:
y = -(1/5) x + 13/5
Obtener mediante métodos analíticos las distancia entre los puntos C y A, siendo las coordenadas rectangulares de C = (-2, -3) y las de A = (3,2).
La fórmula de la distancia euclidiana entre estos dos puntos se escribe así:
d(A, C)=√((Cx – Ax)^2 + (Cy – Ay)^2)
Sustituyendo sus correspondientes coordenadas rectangulares se tiene:
d(A, C)=√(-2 – 3)^2 + (-3 – 2)^2) = √(-5)^2 + (-5)^2)=5√2 =7,07
Obtener la ecuación de la recta que pasa por el punto C de coordenadas (-2, -3) y el punto P de coordenadas (2, 0).
En primer lugar se obtiene la pendiente de la recta CP:
pendiente= (0 -(-3)) / (2 – (-2)) = ¾
Un punto cualquiera Q de coordenadas rectangulares genéricas (x, y) que pertenezca a la recta CP debe tener la misma pendiente:
pendiente= (y -(-3)) / (x – (-2))= (y +3) / (x +2)
Es decir que la ecuación de la recta CP es:
(y +3) / (x +2) = ¾
una forma alternativa de escribir la ecuación de la recta CP es despejando y:
y = ¾ x – 3/2
Obtener las coordenadas rectangulares del punto de intersección entre las rectas y = -(1/5) x + 13/5 y la recta y = ¾ x – 3/2.
Solución: Por definición, el punto de intersección de las dos rectas comparte la mismas coordenadas rectangulares. Por lo tanto, las coordenadas y en el punto de intersección es idéntico para ambas rectas:
-(1/5) x + 13/5 = ¾ x – 3/2
lo que conduce a la siguiente expresión:
(¾ + ⅕) x = 13/5 +3/2
resolviendo la suma de fracciones se obtiene:
19/20 x = 41/10
Despejando x :
x = 82/19 = 4,32
Para obtener el valor y de la intersección se sustituye el valor x obtenido en alguna de las rectas:
y = ¾ 4,32 – 3/2 = 1,74
Esto significa que las rectas dadas se interceptan en el punto I de coordenadas I = ( 4,32 ; 1,74 ).
Obtener la ecuación de la circunferencia que pasa por el punto R de coordenadas rectangulares (3, 4) y que tiene centro en el origen de coordenadas.
Solución: El radio R es la distancia del punto R al origen O de coordenadas (0, 0).
d(R,O) =√((Rx – 0)^2 + (Ry – 0)^2) = √((3 – 0)^2 + (4 – 0)^2)= √(3^2 + 4^2) = √(9 + 16) = √(25)= 5
Es decir, que se trata de una circunferencia de radio 5 centrada en (0,0).
Un punto P cualquiera (x, y) de la circunferencia debe tener la misma distancia 5 al centro (0, 0) por lo que puede escribirse:
d(P, O) = √((x – 0)^2 + (y – 0)^2) = √(x^2 + y^2) = 5
Es decir:
√(x^2 + y^2) = 5
Para eliminar la raíz cuadrada, se eleva al cuadrado ambos miembros de la igualdad obteniéndose:
x^2 + y^2 = 25
Que es la ecuación de la circunferencia.
Con este ejemplo se ilustra la potencia del sistema de coordenada rectangulares, el cual permite determinar objetos geométricos, como la circunferencia sin la necesidad de usar papel, lápiz y compás. Se ha determinado la circunferencia pedida únicamente por métodos algebraicos.
- Arfken G and Weber H. (2012). Mathematical methods for physicists. A comprehensive guide. 7th edition. Academic Press. ISBN 978-0-12-384654-9
- Cálculo cc. Problemas resueltos de coordenadas rectangulares. Recuperado de: calculo.cc
- Weisstein, Eric W. “Cartesian Coordinates.” From MathWorld-A Wolfram Web. Recuperado de: mathworld.wolfram.com
- wikipedia. Cartesian coordinate system. Recuperado de: en.wikipedia.com
