Ecuación de continuidad: fórmula, aplicaciones, ejercicios resueltos
¿Qué es la ecuación de continuidad?
La ecuación de continuidad, para un fluido incompresible, establece que la masa total de un fluido que circula por un tubo, sin pérdidas ni ganancias, se mantiene constante. En otras palabras, la masa se conserva sin cambios a medida que el fluido se desplaza.
Un fluido incompresible es aquel cuya densidad permanece aproximadamente constante mientras fluye. Por ejemplo, el agua es un líquido considerado incompresible bajo condiciones estándar de presión y temperatura.
Hay una forma matemática de expresar la conservación de la masa, en la ecuación de continuidad, dada por:
A1∙ v1 = A2∙ v2
Donde v1 y v2 representan la velocidad del fluido en dos secciones de una tubería, mientras que A1 y A2 son las respectivas áreas de sección transversal.
El producto del área de sección transversal por la velocidad recibe el nombre de caudal y la ecuación de continuidad implica que, a todo lo largo de la tubería, el caudal es constante. Al caudal también se le conoce como razón de flujo de volumen, se comprende al observar con cuidado la expresión anterior, cuyas dimensiones son de volumen por unidad de tiempo.
Fórmula
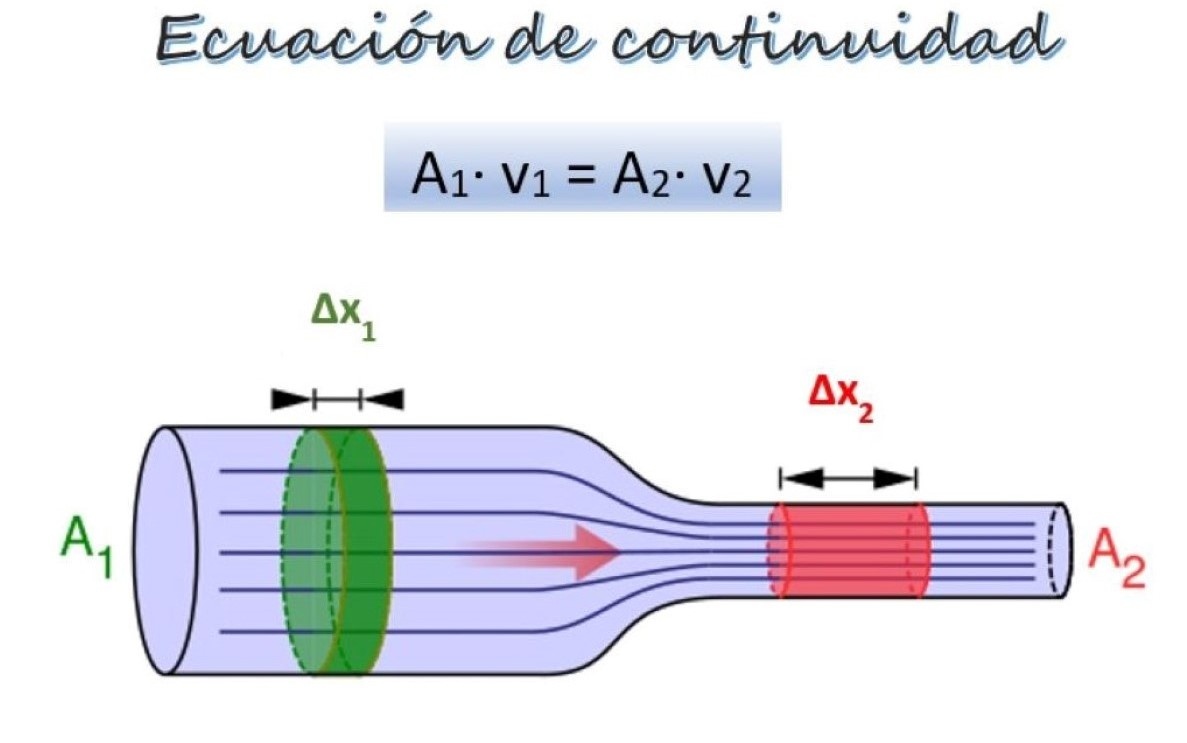
En la imagen superior hay una tubería con dos secciones de diferente diámetro y a la misma altura, aunque podrían estar a alturas diferentes sin que represente problema.
En la sección 1, más ancha, el área de sección transversal es A1 y el fluido se mueve con velocidad v1, mientras que en la sección 2, más estrecha, el área de sección transversal es A2 y la velocidad del fluido es v2.
Una porción de masa Δm1 (verde) se mueve por la sección 1 en un tiempo Δt. Durante este lapso, la porción Δm2 (rojo) viaja por la sección 2. Como el fluido es incompresible, su densidad es la misma en todos sus puntos, así que partiendo de la definición de la densidad:
Δm1 = ρ∙V1
Donde el volumen V1 es el producto entre el área de la sección transversal y la distancia Δx1:
Δm1 = ρ∙ (A1 ∙ Δx1)
Pero dado que:
Δm1 = ρ∙ A1 ∙ Δx1 = ρ∙A1 ∙ (v1 ∙Δt)
Análogamente se escribe la porción Δm2 que fluye al mismo tiempo por la sección 2:
Δm2 = ρ∙A2 ∙ Δx2 = ρ∙A2 ∙(v2 ∙Δt)
Por conservación de la masa:
Δm1 = Δm2
Y:
ρ∙A1 ∙ v1 ∙Δt = ρ∙A2 ∙ v2 ∙Δt
Como Δt y ρ se cancelan, resulta:
A1 ∙ v1 = A2 ∙ v2
El caudal Q
El producto del área de la sección transversal A por la velocidad del fluido v se denomina caudal y se denota como Q. Equivale al volumen de fluido por unidad de tiempo a través de la tubería, o razón de flujo de volumen:
- 1 m3/s = 264.172 gal/s
- 1 L/s = 0.001 m3/s
- 1 ft3/s = 0.0283168 m3/s
- 1 L/s = 0,264172 gal/s
- 1 m3/s = 15850,3 gal/min
Nótese que, al disminuir la sección transversal del tubo, la velocidad del fluido aumenta, y viceversa, si aumenta la sección transversal, entonces la velocidad disminuye para que el caudal se mantenga constante.
Aplicaciones y ejemplos
La ecuación de continuidad se utiliza en el análisis del flujo de fluidos, en combinación con la ecuación de Bernoulli, en la que se toman en cuenta las variaciones de la velocidad del fluido en las diferentes secciones, así como los cambios de presión y el efecto de la altura.
Ejemplo 1
En la familiar manguera de jardín, cuando el agua sale normalmente el chorro tiene un cierto alcance, pero si se pone el dedo en la salida de la manguera, disminuyendo el orificio de salida, el alcance del chorro es mayor.
Aquí se cumple la ecuación de continuidad, ya que, al disminuir el área de la boquilla de salida, la velocidad del chorro aumenta para que el producto área por velocidad se mantenga constante.
Ejemplo 2

Otro ejemplo donde se pone en evidencia la ecuación de continuidad es el chorro de agua que se estrecha a medida que cae, debido al aumento de la velocidad del agua durante la caída.
De esta manera se mantiene constante el caudal, mientras el chorro siga fluyendo en régimen laminar, es decir el agua caiga suavemente sin turbulencias ni remolinos.
Ejercicios resueltos
Ejercicio 1
Circula agua por una tubería de 20 cm de diámetro. Sabiendo que el caudal es de 2000 L/s, hallar la velocidad del agua en la tubería.
Solución
Conviene expresar todo en unidades del Sistema Internacional. En primer lugar, se calcula el área de sección transversal de la tubería, recordando que el radio es la mitad del diámetro:
A = π∙ (D/2)2
D = 20 cm = 0.2 m
Por lo tanto, el área es:
A = π∙ (D/2)2 = A = π∙ (0.2 m /2)2 = 0.0314 m2.
El caudal se expresa en m3/s con ayuda del factor de conversión apropiado:
Q = 2000 L/s = 2 m3/s
De la fórmula Q = A ∙ v se despeja la velocidad con la que circula el fluido por la tubería:
Ejercicio 2
Se tiene una tubería de sección transversal variable a través de la cual fluye agua. En determinado punto, el área de la sección transversal es 0.070 m2 y la rapidez del agua es 3.50 m/s. Calcular:
a) La rapidez del agua en otro punto de la tubería cuya área de sección transversal es 0.105 m2.
b) El volumen de agua que se descarga por un extremo abierto en 1 hora.
Solución a
Se emplea la ecuación de continuidad, igualando el caudal del primer punto con el caudal del segundo. El caudal es:
Q = A ∙ v
Por continuidad:
Q1 = Q2
A1 ∙ v1 = A2 ∙ v2
Ahora sustituyen los datos suministrados por el enunciado:
- A1 = 0.070 m2
- v1 = 3.50 m/s
- A2 = 0.105 m2
- v2 =?
Y se despeja v2:
Solución b
Dado que el caudal también es el volumen por unidad de tiempo, se tiene que:
V = Q∙Δt = (A∙v) Δt
El caudal Q se puede calcular con los datos del punto 1 o los del punto 2, ya que es el mismo en ambos puntos:
Q = A1 ∙ v1 = 0.070 m2 ∙ 3.50 m/s = 0.245 m3 / s
Sabiendo que 1 hora = 3600 s, el volumen de agua descargado es:
V = Q∙Δt = (0.245 m3 / s) × (3600 s) = 882 m3
En 1 hora se descargan 882 m3 de agua por la tubería.
