Tau de Kendall (II)
Es una medida de dependencia no paramétrica que identifica los pares concordantes y discordantes de dos variables. Una vez identificados, se calculan los totales y se hace el cociente.
En otras palabras, asignamos una clasificación a las observaciones de cada variable y estudiamos la relación de dependencia entre dos variables dadas.
Hay dos maneras de calcular la Tau de Kendall; nosotros optamos por calcular la relación de dependencia una vez ordenadas las observaciones de cada variable. En nuestro ejemplo, veremos que ordenamos en orden ascendente las clasificaciones de la columna X.
Las correlaciones clasificadas son una alternativa no paramétrica como medida de dependencia entre dos variables cuando no podemos aplicar el coeficiente de correlación de Pearson.
Estos son los resultados a los que hemos hecho referencia en el primer artículo –> Tau de Kendall (I):
| Estación de esquí (i) | X | Z | C | NC | |
| A | 1 | 1 | 6 | 0 | |
| B | 2 | 3 | 5 | 0 | |
| C | 3 | 4 | 5 | 1 | |
| D | 4 | 2 | 4 | 0 | |
| E | 5 | 7 | 4 | 1 | |
| F | 6 | 6 | 4 | 1 | |
| G | 7 | 5 | 43 | 3 | TOTAL |
- El par BC-CB es un par discordante. Anotamos 1 en la columna NC y paralizamos el contador en la última posición hasta volver a encontrar un par concordante. En este caso, hemos paralizado el número de pares concordantes en 5 hasta la estación D. La estación D solo puede formar 4 pares concordantes: AD-DA, DE-ED, DF-FD, DG-GD.
Otro par discordante sería EF-FE:
- El par EF-FE es un par discordante. Anotamos 1 en la columna NC y continuamos arrastrando el número 4 de pares concordantes que pueden formarse. Los pares concordantes de la estación E serían: EA-AE, EB-BE, EC-CE, ED-DE porque EF-FE es discordante.
- El par FG-GF es un par discordante. Anotamos 1 en la columna NC y continuamos arrastrando el número 4 de pares concordantes que pueden formarse. Los pares concordantes de la estación F s (no hemos variado el en lugar de un 4. Los pares concordantes que podria mos que antes (no hemos variado el serían: FA-AF, FB-BF, FC-CF, FD-DF porque FG-GF es discordante.
Calculamos la Tau de Kendall
La Tau de Kendall no tiene secreto más allá de ser el cociente de los pares concordantes y discordantes de una muestra de observaciones.
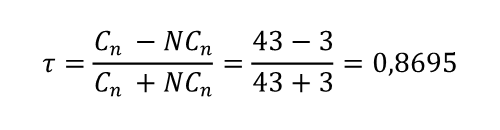
Interpretación
Nuestra pregunta incial era: ¿existe una relación de dependencia entre las preferencias de los esquiadores aficionados al esquí alpino y los esquiadores aficionados al esquí nórdico en las estaciones de esquí dadas?
En este caso, tenemos una dependencia entre las dos variables de 0,8695. Un resultado muy cerca del límite superior. Este resultado nos dice que los esquiadores aficionados al esquí alpino (X) y los esquiadores aficionados al esquí nórdico (Z) han clasificado las estaciones con clasificaciones parecidas.
Sin tener que hacer ningún tipo de cálculo podemos ver que las primeras estaciones (A,B,C) reciben las mejores puntuaciones por parte de los dos colectivos. En otras palabras, las valoraciones de los esquiadores siguen la misma dirección.
Comparación: Pearson vs Kendall
Si calculamos el coeficiente de correlación de Pearson dadas las observaciones anteriores y lo comparamos con la Tau de Kendall, obtenemos:
En este caso, la Tau de Kendall nos dice que hay una relación de dependencia más fuerte entre las variables X y Z comparada con el coeficiente de correlación de Pearson: 0,8695 > 0,75.
Si las observaciones atípicas tuvieran mucha influencia en los resultados, encontraríamos gran diferencia entre Pearson y Spearman y, por tanto, deberíamos utilizar Spearman como medida de dependencia.
