Punto de inflexión

El punto de inflexión, en otras palabras, es ese momento en el que la función cambia de tendencia.

Cabe destacar que una función puede tener más de un punto de inflexión, o no tenerlos del todo. Por ejemplo, una recta no tiene ningún punto de inflexión.

Asimismo, en términos matemáticos, el punto de inflexión se calcula igualando la segunda derivada de la función a cero. Así, despejamos la raíz (o raíces) de esa ecuación y la(s) llamaremos Xi.

Luego, reemplazamos Xi en la tercera derivada de la función. Si el resultado es diferente a cero, estamos frente a un punto de inflexión.

Sin embargo, si el resultado es cero, debemos reemplazar en las derivadas sucesivas, hasta que el valor de esta derivada, ya sea la tercera, cuarta o quinta, sea diferente a 0. Si la derivada es impar se trata de un punto de inflexión, pero si es par no.

A continuación, veamos un ejemplo.

Supongamos que tenemos la siguiente función:

y=2x⁴+5x³+9x+14

Primera derivada: y’=8x³+15x²+9

Segunda derivada: y»=24x²+30x=0

24x²=-30x

24x=-30

x=-30/24

Xi=-1,25

Luego, reemplazamos Xi en la tercera derivada:

y»’=48x

y»’=48*(-1,25)=-60

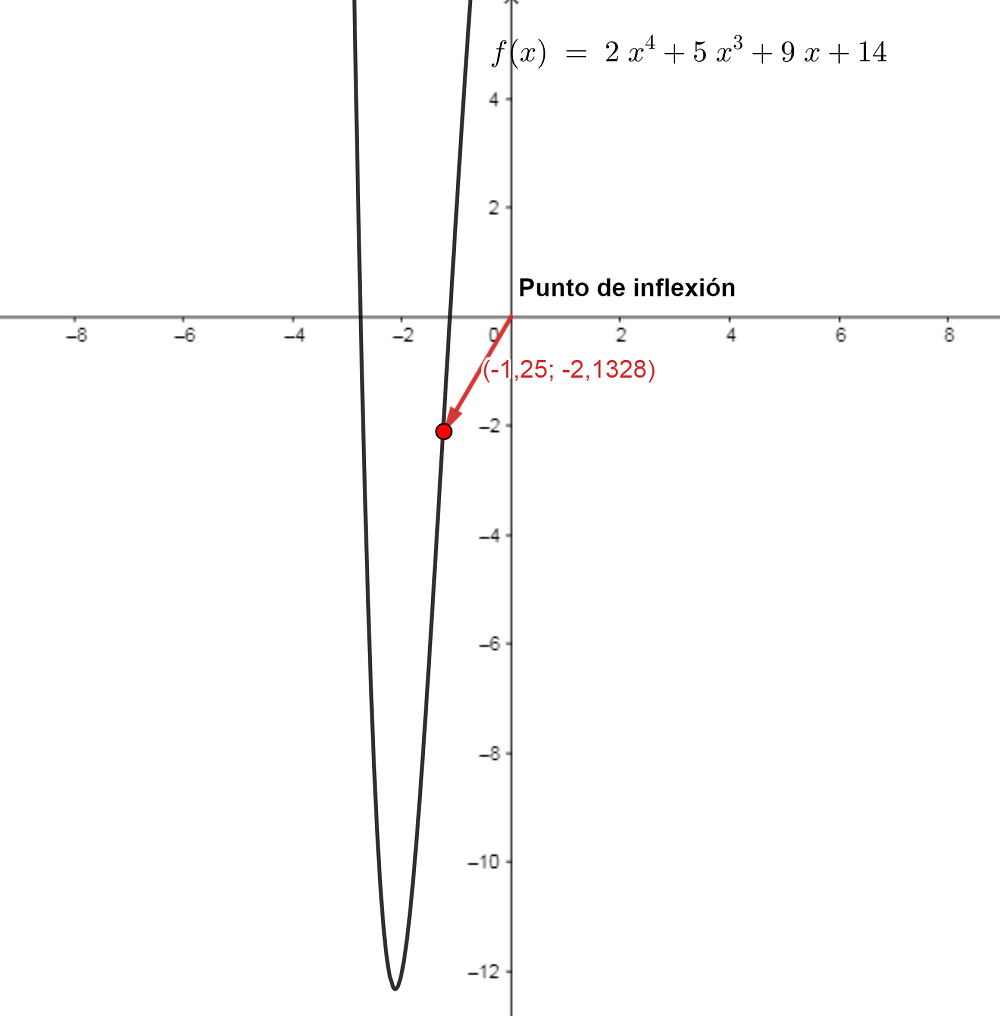
Como el resultado es diferente a cero, nos encontramos frente a un punto de inflexión que sería cuando x es igual a -1,25 e y es igual a -2,1328, como lo demostraremos a continuación:

y=2x⁴+5x³+9x+14

y=2(-1,25)⁴+5(-1,25)³+9(-1,25)+14

y=(2*2,4414)+(5*-1,9531)+(9*-1,25)+14

y=4,8828+(-9,7656)+(-11,25)+14

y=-2,1328

En esta gráfica se observa que la función tiene un punto de inflexión:

Ahora, veamos otro ejemplo:

y=x⁴-54x²

y’=4x³-108x

y»=12x²-108=0

x²=108/12

x²=9

Xi=3 y -3

Luego, reemplazamos las dos raíces encontradas en la tercera derivada:

y»’=24x

y»’=24×3=72

y»’=24x-3=-72

Como el resultado es diferente a cero, tenemos dos puntos de inflexión en (3;-405) y (-3;-405). El dato de -405 resulta de reemplazar 3 y -3, respectivamente, en la función de y.

y=x⁴-54x²=3⁴-54*3²=81-486=405 (El resultado es el mismo con -3)

Para complementar la información, te invitamos a visitar el artículo de inflexión, donde abarcamos de forma más general dicho concepto:

El artículo contiene información incorrecta. El artículo describe lo que se conocen como extremos (máximos y mínimos). Los extremos y los puntos de inflexión son diferentes, por ejemplo la función f(x)=x^3 tiene un punto de inflexión en x=0 que no es extremo.

Una referencia que pueden consultar para explicar los puntos de inflexión es Stewart, "Cálculo de una variable" 6.ed. página 291.

Gracias.

Por favor da de baja el material. Tienes varios errores el más grave es que señalas un extremo de la función como punto de inflexión.

Te sugiero que uses libros de matemáticas o cálculo para generar las entradas, por ejemplo Stewart "cálculo trascendentes tempranas"

Hola Pablo,

Me gustaría saber dónde has localizado los fallos para corregirlos y actualizar el artículo.

Muchas gracias por tu colaboración, un saludo de parte de todo el equipo de Economipedia 🙂

Hola,

Gracias por las observaciones. Se actualizó el artículo para evitar las confusiones.

Saludos

Guillermo, te recomiendo que cambies la escala del primer y del tercer gráfico porque no se pueden ver bien las concavidades y se presta a confusión. En el primer gráfico parece que estas indicando que un mínimo es lo mismo que un punto de inflexión.

Hola,

Gracias por la observación, efectivamente, había un error y los gráficos fueron retirados. Para entender visualmente el punto de inflexión puedes mirar el gráfico del ejemplo.

Saludos