Número pi
El número pi es un número decimal infinito no periódico famoso por aparecer en muchas fórmulas matemáticas en los campos de la geometría, teoría de los números, probabilidad, análisis matemático y en aplicaciones de física.
En otras palabras, el número pi es un número decimal que no puede expresarse en forma de fracción de enteros (número irracional) y aparece en muchas fórmulas matemáticas.
Símbolo de pi
El número pi se representa mediante el siguiente símbolo:
Los primeros dígitos del número pi son:
3,141592653589793115997963468544185161590576171875…
Es importante no caer en la tentación de aproximar pi a 3 o a 3,14:
El problema de aproximar aparece cuando queremos resolver un problema práctico real y tenemos que trabajar con el número pi. Por ejemplo, suponemos que queremos cortar una lámina de madera para hacer una mesa redonda. ¿Creéis que si calculamos el área de la superficie de la mesa empleando pi=3, la mesa será la misma?
La mayoría de calculadoras tienen una tecla especial para este número y con tan solo activarla nos ahorramos escribir los decimales de pi. Los problemas complejos se resuelven directamente mediante computación.
Historia del número pi
El número pi empezó su trayectoria en el ámbito de la geometría donde ganó importancia y en el siglo XVII se profundizó en el cálculo infinitesimal hasta llegar a nuestros tiempos con los ordenadores.
Arquímedes realizó la primera estimación consistente del número pi a través de dibujar polígonos regulares cada vez con más lados. El resultado fue que los polígonos regulares de 96 lados se ajustaban dentro de una circunferencia y que los que tenían más lados superaban dicha circunferencia. De esta forma establecieron los siguientes límites con los perímetros de los polígonos regulares empleados:
Número pi en geometría
En el ámbito de la geometría, hay algunas fórmulas que llevan el número pi implícito. Una pista para recordar qué formas llevan el número pi es dibujarlas. Cualquier figura o cuerpo geométrico que tenga un círculo o una esfera, aparecerá el número pi en su fórmula.
Esto es posible ya que tanto el perímetro como el área de un círculo necesitan el número pi para ser calculados. Por ejemplo, el cuerpo geométrico cono, tiene como base un círculo, y por tanto, encontraremos el número pi en su área y en su volumen.
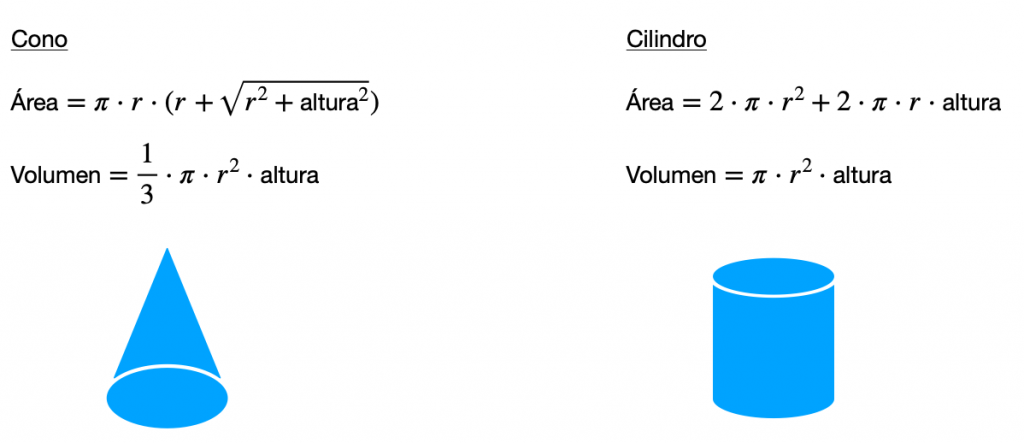
Ejemplo del número pi
Observa las siguientes figuras y cuerpos geométricos. Determina si su fórmula llevará el número pi o no.
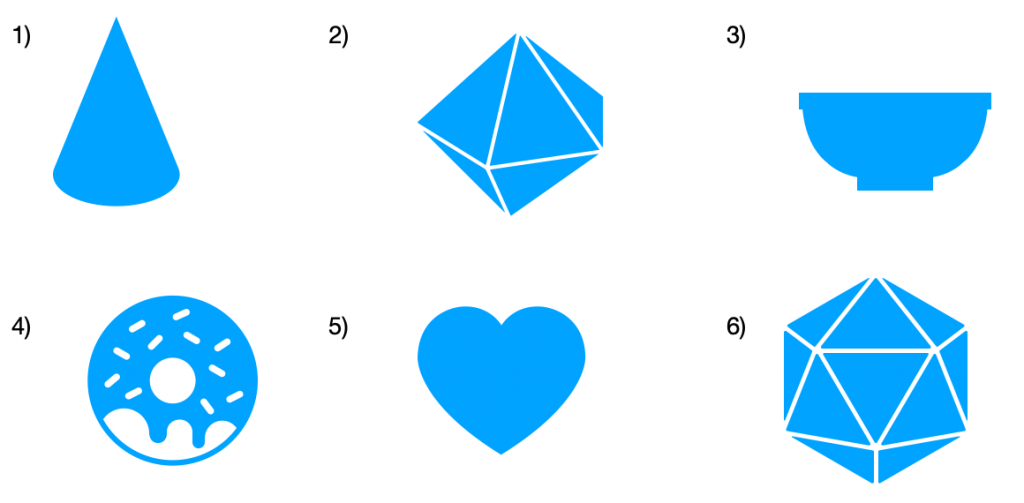
Respuesta:
- Sí, es un cono y su base es un círculo.
- No, no tiene ninguna circunferencia ni círculo.
- Sí, la base es una circunferencia.
- Sí, tanto el área como el perímetro o volumen son redondos.
- Sí, el corazón tiene dos círculos implícitos.
- No, no tiene ninguna circunferencia ni círculo.
