Número áureo
El número áureo o razón áurea es un número irracional que representa la igualdad entre la proporción de dos segmentos de diferente longitud y el cociente de la suma de ellos y el segmento con más longitud.
En otras palabras, el número áureo es la igualdad entre la división de dos segmentos de longitud distinta y la división de la suma de los dos segmentos y el segmento más largo.
Este número también recibe los nombres de número de oro o proporción divina, debido a sus aplicaciones a lo largo de la historia.
Notación del número áureo
El número áureo se representa mayoritariamente con la letra griega phi. También existen asociaciones hacia a la letra tau.
La razón áurea puede expresarse mediante radicales, es decir, en su expresión matemática aparecerá una raíz, o en números decimales:
Demostración algebraica del número áureo
Los orígenes de este número irracional pertenecen al campo de la geometría, pues esta proporción aparece cuando se trabaja con dos segmentos de distinta longitud. ¿Cómo puede pasarse de dos segmentos a un número decimal? A continuación, la demostración.
Suponemos que tenemos dos segmentos, X e Y, de distinta longitud, y donde el segmento X es más largo que el segmento Y.

La proporción áurea cumple que:
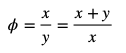
A partir de aquí se puede desarrollar la igualdad haciendo en producto cruzado:
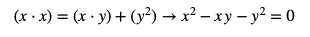
El resultado es una ecuación de segundo grado que podemos resolver mediante su fórmula cerrada:
Entonces, Y pasa dividendo al otro lado del igual y encontramos la ecuación inicial:
De esta forma hemos demostrado la intersección entre la fórmula de los segmentos geométricos y el origen del número irracional que conocemos.
Propiedades del número áureo
A continuación, mostramos las propiedades del número áureo.
Propiedad 1
- Este número es el único número real positivo que cumple la siguiente ecuación:
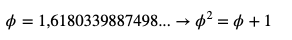
Esta ecuación puede deducirse separando la triple igualdad en dos ecuaciones:
La ecuación 2 puede simplificarse separando la fracción en la suma de dos fracciones. Luego, podemos ver que la ecuación 2 está compuesta por la inversa de la ecuación 1, y podemos sustituir por phi elevado a -1. Entonces, para no dejar la ecuación con un exponente negativo, multiplicaremos ambos lados del igual por phi, resultando en la ecuación inicial de esta propiedad.
Propiedad 2
- También pueden escribirse las siguientes igualdades:
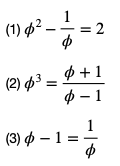
Las tres igualdades pueden deducirse de la ecuación inicial de la primera propiedad.
Proporción áurea en la naturaleza
Podemos encontrar el número áureo en objetos naturales que sigan la sucesión numérica de Fibonacci, en la cual la división de dos números consecutivos en la serie tiende a la proporción áurea.
La sucesión de Fibonacci es la sucesión infinita de los siguientes números naturales: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377… Si nos fijamos bien, cada número es la suma de los dos anteriores. Y, para llegar a la proporción áurea, tendremos que dividir cada número con el anterior.
| Sucesión de Fibonacci | Proporción |
|---|---|
| 1 | 0 |
| 1 | 100,0% |
| 2 | 200,0% |
| 3 | 150,0% |
| 5 | 166,7% |
| 8 | 160,0% |
| 13 | 162,5% |
| 21 | 161,5% |
| 34 | 161,9% |
| 55 | 161,8% |
| 89 | 161,8% |
| 144 | 161,8% |
| 233 | 161,8% |
| 377 | 161,8% |
| 610 | 161,8% |
Como podemos observar, la división de un número por el anterior de la sucesión, tiende a dar como resultado el número áureo.
También aparece en la sucesión numérica de Lucas.
Ejemplo de número áureo
Demuestra que la tercera ecuación de la segunda propiedad es una derivación de ecuación de la primera propiedad:

