Modelo GARCH
El modelo GARCH es un modelo autorregresivo generalizado que captura las agrupaciones de volatilidad de las rentabilidades a través de la varianza condicional.
En otras palabras, el modelo GARCH encuentra la volatilidad promedio a medio plazo mediante una autorregresión que depende de la suma de perturbaciones rezagadas y de la suma de varianzas rezagadas.
Si vemos la volatilidad histórica ponderada comprobamos la referencia a los modelos ARCH y GARCH para ajustar el parámetro p a la realidad. El parámetro p es la ponderación para cada distancia entre la observación t y su media al cuadrado (perturbación al cuadrado).
Artículos recomendados: volatilidad histórica, volatilidad histórica ponderada, autorregresión de primer orden (AR(1)).
Significado
GARCH significa modelo autorregresivo generalizado condicional heterocedástico, del inglés, Generalized AutoRegressive Conditional Heteroscedasticity.
- Generalizado porque tiene en cuenta tanto las observaciones recientes como las históricas.
- Autorregresivo porque la variable dependiente se regresa en sí misma.
- Condicional porque la varianza futura depende de la varianza histórica.
- Heterocedástico porque la varianza varía en función de las observaciones.
Tipos de modelos GARCH
Los tipos de modelos GARCH principales son:
- GARCH: GARCH simétrico.
- A-GARCH: GARCH asimétrico.
- GJR-GARCH: GARCH con umbral.
- E-GARCH: GARCH exponencial.
- O-GARCH: GARCH ortogonal.
- O-EWMA: GARCH ortogonal exponencial de media móvil ponderada.
Aplicaciones
El modelo GARCH y sus extensiones son utilizados por su capacidad de predecir la volatilidad a corto y medio plazo. Aunque utilizamos Excel para hacer los cálculos, se recomiendan programas estadísticos más complejos como R, Python, Matlab o EViews para realizar estimaciones más precisas.
Las tipologías de GARCH se utilizan en función de las características de las variables. Por ejemplo, si estamos trabajando con bonos sobre tipos de interés con distintos vencimientos, utilizaremos GARCH ortogonal. Si estamos trabajando con acciones utilizaremos otro tipo de GARCH.
Construcción del modelo GARCH
Definimos:

Los rendimientos de los activos financieros oscilan en torno a su promedio siguiendo una distribución de probabilidad normal de media 0 y varianza 1. Entonces, el rendimiento de los activos financieros es completamente aleatorio.
Definimos la varianza histórica:
Para construir un GARCH en un período de tiempo (t-p) y (t-q)necesitamos:
- Perturbación al cuadrado de ese período de tiempo (t-p).
- Varianza histórica anterior a ese período de tiempo (t-q).
- Varianza de un período de tiempo inicial como término constante.
ω
Matemáticamente, GARCH(p,q):
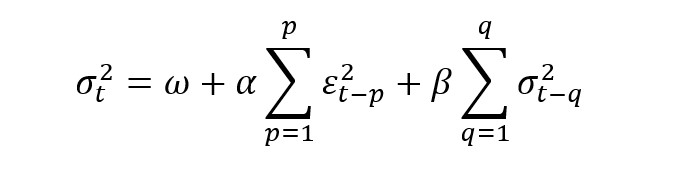
Los coeficientes ω, α, β, los encontramos los encontramos utilizando técnicas econométricas de estimación de Máxima Verosimilitud. De esta forma encontraremos la ponderación para la varianza de las observaciones recientes y para la varianza de las observaciones históricas.
Ejemplo práctico
Suponemos que queremos calcular volatilidad de la acción AlpineSki para el siguiente año 2020 mediante GARCH(1,1), es decir, cuando p=1 y q=1. Disponemos de datos desde 1984 hasta 2019.
GARCH(p,q), cuando p=1 y q=1:
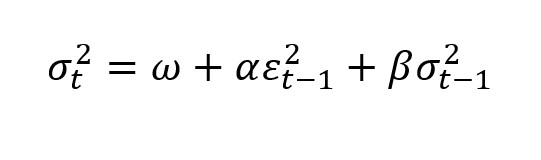
Sabemos que:

Mediante Máxima Verosimilitud hemos estimado los parámetros ω, α, β,:
ω = 0,02685 α = 0,10663 β = 0,89336
Entonces,

Dada la muestra anterior y según el modelo, podemos decir que se estima una volatilidad para 2020 de la acción AlpineSki próxima al 16,60%.
