Modelo de retardos distribuidos finitos

Como todo modelo econométrico, un modelo de retardos distribuidos finitos, estará compuesto por una variable explicada o dependiente y una o más variables explicativas. Es decir, tiene la forma matemática tal que:

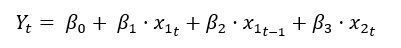
Cómo podemos comprobar, el modelo tiene el mismo aspecto matemático que un modelo econométrico básico. Ahora bien, existen dos diferencias. La primera es que aparece una letra pequeña ‘t’ en la parte inferior. Esta letra se llama subíndice y hace referencia al tiempo. Aparece cuando trabajamos con datos de serie temporal. Por su parte, la segunda diferencia es que una de las variables lleva a la letra ‘t’ acompañada de un menos 1. ¿Qué significa el menos 1? El menos 1 es lo que se llama un retardo.

Un retardo hace referencia a algo del pasado. Es algo que ocurre con efecto retardado. Es lo contrario de efecto inmediato o contemporáneo.

Este efecto retardado puede darse después de uno o más periodos. Además, aunque en el ejemplo inicial tan solo una variable presenta retardos, concretamente un retardo, el retardo puede estar presente en más variables explicativas. Otro detalle que merece la pena destacar es que puede haber un retardo (t-1) o más (por ejemplo, t-3).

Uno de los detalles fundamentales de este tipo de modelos econométricos es interpretarlos correctamente. Aunque no sepamos calcularlos, si sabemos interpretarlos, podremos entender muchos estudios económicos. Para aprender a interpretarlos vamos a proponer el siguiente modelo base:

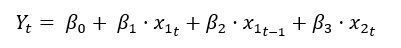
Como todo modelo econométrico, este modelo contiene las siguientes variables:

Y: Es la variable explicada. Puede ser cualquier variable económica que pretendamos predecir, estimar o explicar.

Beta cero: Es el término constante de la ecuación, no tiene significado económico. Su inclusión en la ecuación es por cuestiones matemáticas.

Beta uno: Es el coeficiente cuyo valor explica la relación que tiene la variable explicativa x₁ sobre la variable explicada Y en el momento t.

X1: Se trata de una de las variables que pretende explicar el comportamiento de la variable Y.

Beta dos: Es el coeficiente cuyo valor explica la relación que existe entre la variable explicativa x₁ en el periodo anterior (t-1) y las fluctuaciones de la variable Y.

X2: Es la segunda variable que intenta explicar el comportamiento de Y.

Beta tres: Es el coeficiente cuyo valor explica la relación que existe entre la variable explicativa x₂ y la variable Y.

Subíndice ‘t’: hace referencia al tiempo. Ese subíndice bien podría tomar valores de un año determinado o de un mes determinado.

Aunque en este modelo base solo hemos incluido un retardo en la variable explicativa x₁, podríamos haber incluido más variables explicativas con más retardos. Al final del artículo, veremos ejemplos de posibles de este tipo.

Dentro de los modelos de retardos distribuidos finitos podemos encontrar dos grandes tipos:

• Modelo de retardos distribuidos finitos de orden «q»: Son los que hemos visto hasta ahora. El orden hace referencia al máximo retardo de un modelo. Por ejemplo, un modelo que presente como máximo 3 retardos en alguna de sus variables explicativas se dice que es de orden 3.

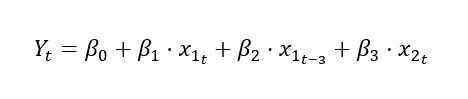
Podemos introducir tantos retardos como queramos, consecutivos o no, en una o más variables explicativas. El orden siempre irá determinado por el máximo retardo. En el caso anterior, 3.

• Modelo de endógena retardada: Un modelo de endógena retardada es aquel en el que al menos una de las variables explicativas es la variable explicada con un efecto retardado. Por ejemplo, imaginemos que queremos explicar en un modelo el PIB. Además de otras variables explicativas, para que el modelo sea de endógena retardada, el modelo debe tener una variable explicativa que sea la variable PIB hace uno o más periodos.

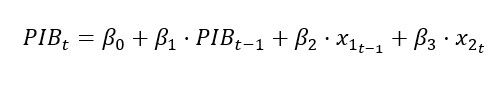
Para que un modelo sea considerado de endógena retardada es suficiente con que la variable explicada, se encuentre como explicativa con al menos un periodo de retardo. En nuestro caso, aparte de cumplirse esa condición, también tenemos un retardo en la variable x₁. Lo anterior no quita generalidad.

En definitiva, el modelo de endógena retardada es un modelo de retardos distribuidos finitos con la particularidad de que la variable explicada, en nuestro caso el producto interior bruto (PIB), aparece como explicativa. Y además, aparece con al menos un retardo.