Minimax

Para verlo de otro modo, el método minimax consiste en cómo tomar la mejor decisión suponiendo que el otro jugador escogerá el peor escenario para ti.

Debemos tomar en cuenta que este método es aplicable en un juego bipersonal (dos jugadores) y que no es cooperativo, sino un juego de suma cero. Esto quiere decir que lo que gana un jugador lo pierde el otro y viceversa. En consecuencia, cada agente estará interesado en maximizar su propia utilidad, aunque eso perjudique al otro.

En este punto, debemos recordar además que la teoría de juegos es una rama de las matemáticas y de la economía que estudia la elección que optimiza la situación de un individuo cuando los costes y los beneficios no están fijados de antemano, sino que dependen de las decisiones de otros.

Podemos observar cómo se aplica el método minimax en un árbol de decisión con varios nodos. El juego comienza abajo y termina con un resultado en el nivel superior.

En la base del árbol, el adversario hace el primer movimiento, por lo que se espera el peor resultado. Luego, en el segundo nivel, le toca al jugador x que buscará maximizar su beneficio, tomando en cuenta la decisión anteriormente tomada por el oponente.

En el tercer nivel, vuelve a ser turno del adversario y así sucesivamente. A continuación, mostraremos un ejemplo.

En el siguiente árbol de decisión, mostramos los resultados obtenidos por el jugador x en cada momento del juego. En la base, en el primer nivel, toma la decisión el oponente. Por esa razón, se dan los escenarios en los que el jugador puede perder -10 o ganar 5.

En el segundo nivel, le toca al jugador x, por lo que maximizará su beneficio. Entre perder 10 o ganar 1, ganará 1. Asimismo, entre ganar 5 o 7, ganará 7.

Luego, le vuelve a tocar al adversario, por lo que se darán los escenarios en los que el jugador x tiene el peor resultado, -3 y 4, dependiendo del caso. Finalmente, entre perder 3 o ganar 4, el jugador x tomará la decisión que permitirá lo segundo.

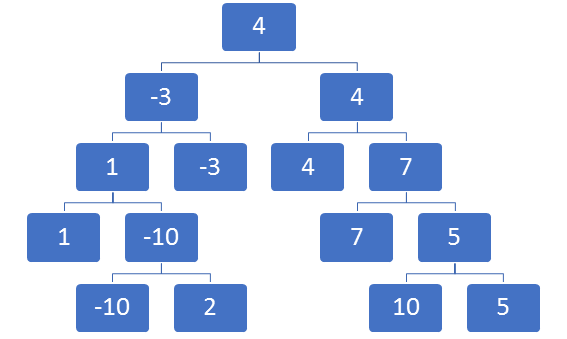
Debemos tomar en cuenta que los valores de cada nodo dependerán de una función de utilidad.

Para entender mejor el árbol, supongamos que en la base la decisión se trata de la distribución del producto. El competidor (el adversario) puede tercerizar la distribución (ver el lado izquierdo del árbol). En ese caso, debe optar, por ejemplo, entre el distribuidor A y B. Así, elige al primero, haciendo que el jugador x pierda 10 (Si escogiera a B, el jugador x ganaría 12).

Sin embargo, quizás el adversario prefiere hacer él mismo la distribución de su mercancía, pudiendo contratar motorizados o comprar una camioneta. De ambos escenarios, elige el primero que es menos favorecedor para el jugador x porque este gana 5 y no 10.