Máximo común divisor (MCD)

Es decir, el máximo común divisor o MCD es la cifra más alta por la cual se puede dividir un conjunto de números, dando como resultado un número entero.

Un divisor puede definirse formalmente como aquel número que está contenido en otro de forma exacta una cantidad n de veces.

Cabe señalar que los números sobre los cuales se calcula el MCD deben ser distintos de cero.

Para explicarlo mejor, observemos un ejemplo. Supongamos que tenemos 35 y 15. Así, observamos cuáles son los divisores de cada uno:

• Divisores de 35 → 35,7,5,1
• Divisores de 15 → 15,5,3,1

Por lo tanto, el máximo común divisor de 35 y 15 es 5.

Vale mencionar que si los divisores comunes de dos números son únicamente 1 y -1 se les denomina «primos entre sí».

Podemos distinguir los siguientes tres métodos para calcular el máximo común divisor:

• Descomposición en factores primos: Se descomponen los números en números primos. Luego, para calcular el MCD, se toman los números comunes elevados a la mínima potencia. Por ejemplo, supongamos que tenemos 216 y 156:

216/2=108

108/2=54

54/2=27

27/3=9

9/3=3

3/3=1

216=(3^3)*(2^3)

156/2=78

78/2=39

39/3=13

13/13=1

156=13*3*(2^2)

Por tanto, el máximo común divisor entre ambos números sería: (2^2)*3=12

Ahora, supongamos que tenemos tres elementos: 315, 441 y 819

315= (3^2)*7*5

441= (3^2)*(7^2)

819= (3^2)*7*13

Entonces, luego de desagregarlos, tomando cada divisor con su mínima potencia, el resultado sería:

MCD= (3^2)*7= 63

• Algoritmo de Euclides: Al dividir a entre b, se obtiene un cociente c y un r. Entonces, el máximo común divisor de a y b es igual que el de b y r. Esto, dada lo siguiente: a=bc+r. Para entenderlo mejor, apliquemos este método al ejemplo mostrado previamente con 216 y 156.

216/156= 1 con residuo de 60

ahora dividimos 156/60=2 con residuo 36

Volvemos a dividir 60/36=1 con residuo 24

Una vez más dividimos 36/24=1 con residuo 12

Y finalmente dividimos 24/12=2 con residuo 0

Por lo tanto, el máximo común divisor es 12. Como podemos observar, debemos dividir hasta que el residuo sea 0 y el último divisor será el MCD.

• En base al mínimo común múltiplo: Se multiplican los números y se divide el resultado entre su mínimo común múltiplo (mcm).

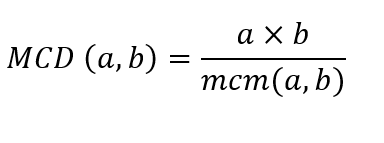
Debemos recordar que el mínimo común múltiplo(mcm) es la cifra más pequeña que satisface la condición de ser múltiplo de todos los elementos de un conjunto de números.

Es decir, volviendo al mismo ejemplo, podemos descomponer de la siguiente forma:

216=(3^3)*(2^3) y 156=13*3*(2^2) 204=3*(2^2)*17 168=3*(2^3)*7

El mínimo común múltiplo sería: (3^3)*(2^3)*13*17*7= 334.152

Entonces: MCD=216*156/2.808=12

Cabe mencionar que este método funciona solo para dos números.