Ejemplo de distribución de Bernoulli
La distribución de Bernoulli es un modelo teórico utilizado para representar una variable aleatoria discreta la cual solo puede finalizar en dos resultados mutuamente excluyentes.
Artículos recomendados: espacio muestral, distribución de Bernoulli y ley de Laplace.
Ejemplo de Bernoulli
Suponemos que somos muy fans de un corredor de una competición ciclista en la cual solo compiten dos corredores. Queremos apostar a que ese corredor gana.

Entonces, si gana será un resultado “éxito” y si pierde será un resultado “no éxito”. Esquemáticamente:

Hemos tratado este ejemplo como un caso dicotómico. Es decir, solo existen dos resultados posibles (para simplificar la situación). En los libros teóricos encontramos el típico ejemplo del lanzamiento de una moneda no trucada que consiste en obtener cara o cruz. Como no hay más resultados posibles, la obtención del parámetro p se vuelve elemental.
En nuestro ejemplo del corredor, también podríamos haber considerado el “no éxito” como la obtención de cualquier otra posición que no fuera el primer puesto. Entonces, el parámetro p cambiaría y sería el número de veces que el corredor pueda quedar primero dividido por el número de posiciones totales. Esquemáticamente:

Aquí el parámetro p no parece muy evidente al principio, pero solo es cuestión de aplicar la ley de Laplace.

Suponemos que solo hay 10 posiciones en las cuales el corredor solo puede obtener una de ellas en la carrera. Entonces,
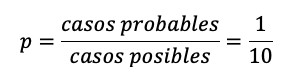
Ejercicio
Calcular la función de distribución del corredor en una competición de 10 corredores.
Función de distribución de Bernoulli
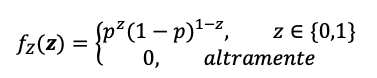
- Planteamiento.
Definimos los dos valores que puede tomar una variable aleatoria que sigue una distribución de Bernoulli.
Z = 1 si el corredor gana la competición = 1r puesto = ÉXITO.
Z = 0 si el corredor pierde la competición = no 1r puesto = NO ÉXITO.
- Asignación y cálculo de probabilidades.
Una vez hemos definido los valores de la Z, asignamos las probabilidades del resultado del experimento:

Arriba en el ejemplo hemos calculado ya las probabilidades mediante la ley de Laplace. El resultado era que p = 1/10 y (1-p)= 0,9.
- Cálculo de la función de distribución.
Ahora solo tenemos que sustituir las variables anteriores en la fórmula de la función de distribución.


Nos podemos fijar en que las expresiones anteriores pueden expresarse también de esta forma:
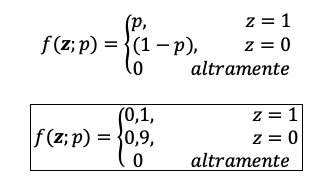
Vemos que utilizando una forma o la otra, la probabilidad de éxito, es decir, la probabilidad de que el corredor gane la competición va a ser siempre p = 1/10 y la probabilidad de no éxito, es decir, la probabilidad de que pierda la competición también será siempre (1-p) = 9/10.
Entonces, el corredor sigue una distribución de Bernoulli con probabilidad p = 0,1:

