Desviación cuartil
La desviación cuartil es una medida estadística de dispersión que devuelve el valor central del rango intercuartílco y se utiliza en conjuntos de datos sesgados.
En otras palabras, la desviación cuartil es calcular la mediana del rango intercuartílico (RIC) y se emplea en conjuntos de datos con bastantes valores extremos.
La forma abreviada de nombrar a la desviación cuartil es DQ.
Rango intercuartílico
El rango intercuartílico es un medida de dispersión de un conjunto de datos generalmente utilizado en el diagrama de caja. En otras palabras, el rango intercuartílico es la diferencia entre el penúltimo y el primer cuartil de una distribución utilizado en el diagrama de caja.
RIC = Q3 – Q1
La ventaja de usar el rango intercuartílico es que se puede calcular la desviación cuartil (DQ) la cual es una medida de dispersión muy adecuada cuando tenemos conjuntos de datos sesgados.
Fórmula de la desviación cuartil
La desviación cuartil se calcula como la división del rango intercuartílico por 2.
DQ = (Q3 – Q1) / 2 = RIC / 2
Dado que solo tenemos en cuenta la dispersión entre el tercero y el primer cuartil, obviamos todos los datos fuera de ese rango. Y, por tanto, todos los valores cercanos de ser extremos. Entonces, si dividimos por dos el rango intercuartílico obtendremos el valor mediano de la dispersión.
Ejemplo de la desviación cuartil
Suponemos que queremos calcular el rango intercuartílico y la desviación cuartil del número de ciclistas que pasan por delante de nuestra casa durante el año.
- Primero, contamos los ciclistas y recogemos la información en una tabla.
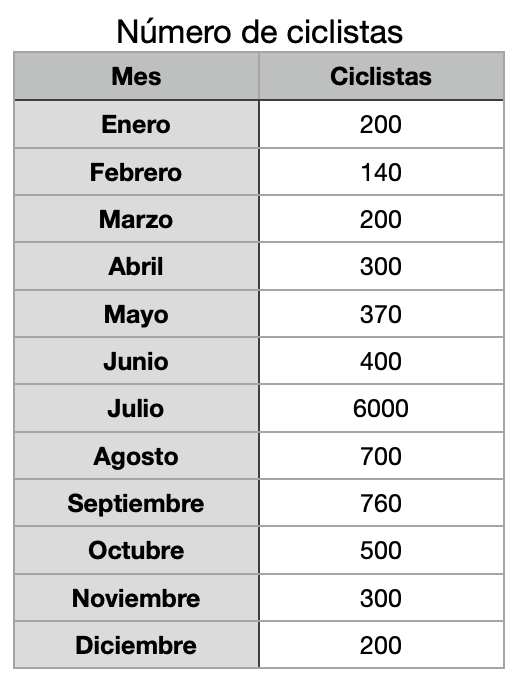
- Segundo, calculamos el primer y tercer cuartil para obtener el rango intercuartílico.
Q3 = 550
Q1 = 200
RIC = Q3 – Q1 = 550 – 200 = 350
- Tercero, calculamos la dispersión cuartil con tan solo dividir entre dos el rango intercuartílico.
DQ = (Q3 – Q1) / 2 = RIC / 2 = 350 / 2 = 175
La dispersión cuartil de este conjunto de datos es 175. Este número es el valor central del rango intercuartílico.
Es importante destacar que el dato del mes de julio es un dato extremo dado que es varias veces superior a todos los demás datos. Entonces, podríamos decir que este conjunto de datos presenta sesgo hacia ese mes. Gracias a la “ignorancia” de la dispersión cuartil hacia los datos extremos, el resultado de esta medida es muy similar a si solo fueran 600 los ciclistas que se circulan en julio. Si en julio solo hubieran 600 ciclistas, la dispersión cuartil sería de 162,5, muy próxima a 175 teniendo en cuenta que el número de ciclistas ese mes es 10 veces menor.
