Crecimiento exponencial

Para explicarlo de otro modo, el crecimiento exponencial implica que el aumento en la función es cada vez más rápido en el tiempo.

En término formales, podríamos decir que existe crecimiento exponencial cuando se cumple lo siguiente:

X_t=X₀.c^rt

Donde:

• X_T = Valor de la función en el momento t.
• X_{0 =} Valor de la función en el periodo 0.
• c = constante mayor a 1.
• r = tasa de crecimiento.
• t = periodo.

Entonces, como podemos deducir, cuanto mayor sea t, mayor será la magnitud por la cual se multiplicará X₀.

Algunos ejemplos de crecimiento exponencial los podemos encontrar en el estudio de la biología, al analizar la reproducción de las bacterias o la dispersión de un virus, por citar algunos casos.

Asimismo, en economía, podemos mencionar a Thomas Malthus, quien advirtió sobre un crecimiento exponencial de la población humana. Esta expansión, según el economista, sobrepasaría la producción de alimentos que, desde su análisis, tendría un crecimiento lineal, es decir, un incremento constante en el tiempo. En cambio, el avance de la población sería cada vez más acelerado.

Malthus advirtió, entonces, que se podría generar una gran crisis de hambruna hacia el año 1880. Sin embargo, esto no llegó a ocurrir. Según los críticos, esto se debería, en resumen, a que se dejaron de lado factores como la creatividad del ser humano (la variable de la tecnología), lo que permitiría incrementar la capacidad de producción de alimentos.

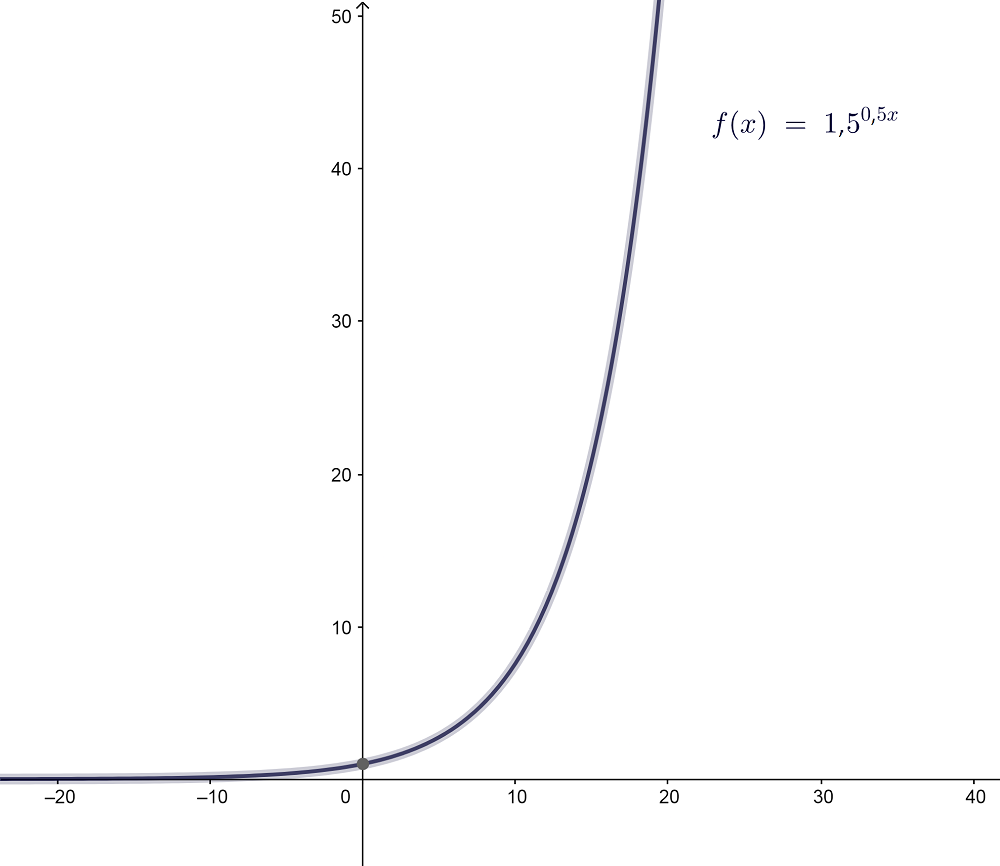
Un caso simple de función con crecimiento exponencial sería f(x)=1,5^0,5x.

Como observamos en el gráfico de abajo, la representación es la de una línea ascendente en forma de J.

Debemos notar que en el ejemplo mostrado el eje vertical es el valor de la función, mientras que el eje horizontal es el momento en el tiempo. Además, el valor inicial de la función en el momento 0 es 1, pues f(x)=1,5^0,5×0=1,5⁰=1.

Este tipo de función contrasta con aquella que tiene un crecimiento lineal, como sería el caso siguiente de y=2x+3.

Para entender mejor la diferencia entre función exponencial y lineal, calcularemos la derivada en cada caso.

Primero, la derivada de la función exponencial respecto a x (el tiempo), se calcularía con la siguiente fórmula:

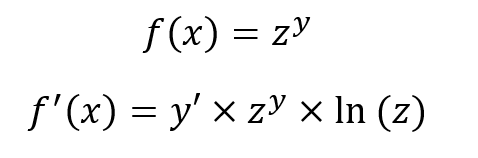
En la fórmula planteada, z es una constante, mientras que y es una función de x, como en el ejemplo mostrado previamente.

Entonces:

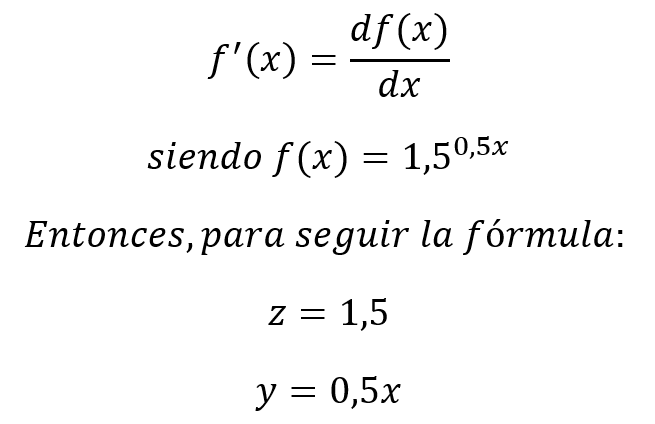
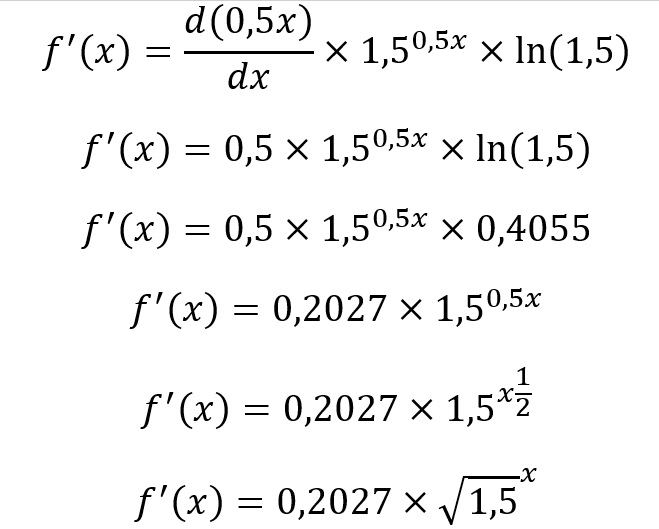
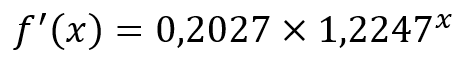
Como podemos observar, la derivada, que es la razón o velocidad de cambio de una función en un determinado punto, depende del valor de x, es decir, del momento en el tiempo. Así, para un periodo más lejano en el futuro, la variación es mayor.

Ahora, en el caso de una función lineal, el cálculo es más simple:

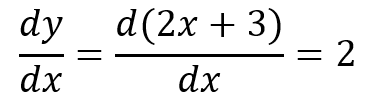
Es decir, en este caso, la tasa de crecimiento es constante, siempre es igual a 2.

Otro concepto de interés es el de decrecimiento (o decaimiento) exponencial, para el cual se tiene la siguiente fórmula, donde el valor de la función se va reduciendo a lo largo del tiempo:

X_t=X₀.e^-rt

Otra forma de entender esta fórmula es que la disminución es proporcional al valor actual de la función.

Cabe aclarar que e es el número de Euler, cuyo valor es, aproximadamente, 2,7183.