Contraste de Durbin Watson
El contraste de Durbin-Watson (DW) se utiliza para realizar una prueba de autocorrelación AR(1) sobre un conjunto de datos. Este contraste se centra en el estudio de los residuos de Mínimos Cuadrados Ordinarios (MCO).
DW es una prueba estadística que contrasta la presencia de autocorrelación en los residuos de una regresión. La principal característica de una serie de datos con los residuos autocorrelacionados es la tendencia definida de los datos.
La autocorrelación se produce cuando las variables independientes tienen una estructura temporal que se repite en determinadas ocasiones a lo largo del tiempo. Entonces, los residuos de hoy (t=2) dependerán de los residuos pasados (t=1) y no se cumplirá el supuesto de independencia del modelo lineal clásico.
Durbin Watson en series financieras
Este problema de autocorrelación podemos encontrarlo en series de datos con una tendencia claramente definida. Por ejemplo, la cotización del índice japonés NIKKEI 225 con el número de forfaits expedido en la estación de esquí de Aspen, EEUU. Ambas series tienen la misma tendencia creciente aunque no compartan, en un principio, ninguna relación. El caso más común de autocorrelación se produce en las series financieras, donde la tendencia de los datos está muy bien definida.
Una solución práctica para reducir la autocorrelación y la heterocedasticidad en las series financieras sería aplicar el logaritmo natural (ln). A través de la primera diferencia,lnPt – lnPt-1 , aislamos las series de su tendencia. En este caso, representa los precios en tiempo t.
El resultado es la distribución DW condicional en Xi que cumple con los supuestos del modelo lineal clásico, con especial importancia el supuesto de normalidad en los residuos.
Este contraste es conocido por los límites superiores e inferiores para valores críticos que dependen del nivel de significación del intervalo de confianza. Estos niveles generales son:
- dU: Límite superior.
- dL: Límite inferior.
Aunque no disponemos de una distribución exacta, dU y dL están definidos en las tablas de DW. Los límites están en función del número de variables (n) y el número de variables explicativas (k).
Procedimiento
1. Ordenamos los residuos en orden temporal tal que
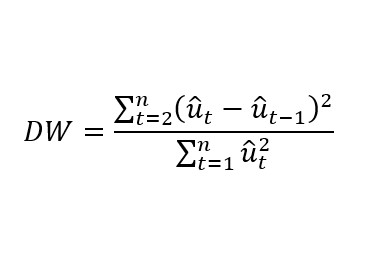
2. Definimos H0 y H1 .

3. Estadístico de contraste t.
4. Regla de rechazo.
En muestras grandes, DW es aproximadamente igual a 2(1-r) donde r es la estimación de primer orden sobre los residuos.
El rango aproximado para DW es [0,4]

- Si 0 ≤ DW < dL → Rechazamos H0
- Si dL < DW < dU → Test no concluyente
- Si dU < DW < Si 4 – dU → No existe autocorrelación de primer orden
- Si 4 – dU < DW < Si 4 – dL → Test no concluyente
- Si 4 – dL < DW ≤ 4 → No tenemos suficientes evidencias significativas para rechazar H0
