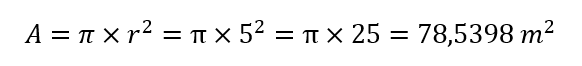Circunferencia
La circunferencia es una figura geométrica plana y cerrada que se caracteriza porque todos los puntos que la conforman se encuentran a la misma distancia del centro. Dicha distancia permanente se denomina radio.
Debemos distinguir la circunferencia del círculo, siendo este último el plano contenido dentro de la primera.
Visto de otro modo, la circunferencia es el perímetro del círculo.
Elementos de una circunferencia
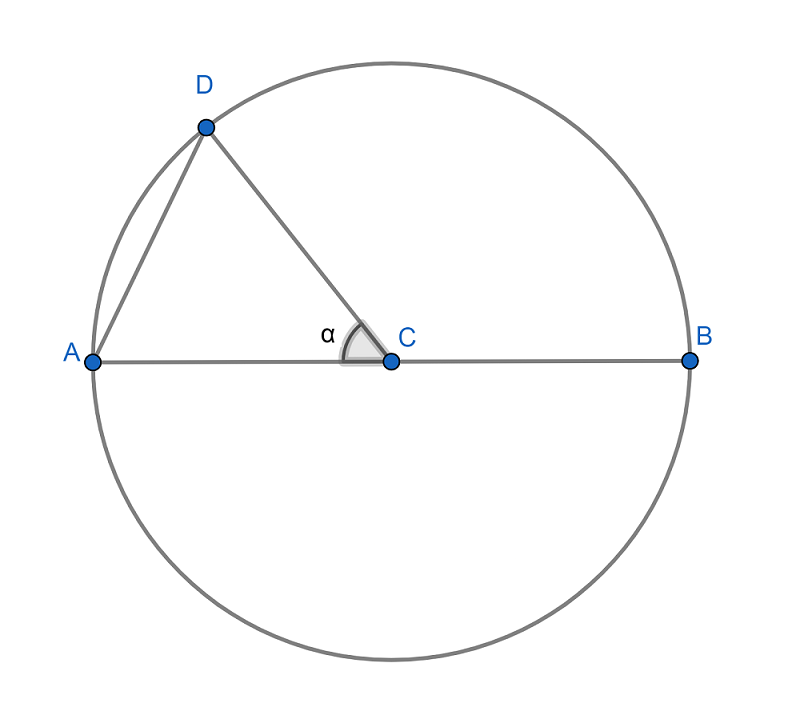
Los elementos de una circunferencia son, guiándonos de la figura inferior, los siguientes:
- Centro(C): Es el punto que se encuentra a la misma distancia (es equidistante) de todos los puntos de la circunferencia.
- Radio(CD): Es el segmento que une el centro de la circunferencia con cualquiera de sus puntos.
- Diámetro(AB): Es el segmento que une dos puntos extremos de la circunferencia, pasando por el centro. Cabe notar que el diámetro el el doble del radio.
- Cuerda(AD): Es el segmento que une dos puntos de la circunferencia, pero a diferencia del diámetro no pasa por el centro de la figura.
- Arco: Es la curva que une los dos extremos de una cuerda, como la porción de la circunferencia de abajo que une los puntos A y D.
- Ángulo central (α): Es el ángulo que se forma entre dos radios de la circunferencia.
- Semicircunferencia: Es la porción de la circunferencia delimitada por dos extremos del diámetro.
Ecuación de la circunferencia
Para explicar la ecuación de la circunferencia, debemos tomar como referencia primero que su centro es la coordenada (a,b) del plano cartesiano. Asimismo, cualquiera de los punto de la circunferencia está en la coordenada (x,y), y el radio de la figura será r. Entonces, se cumplirá que:
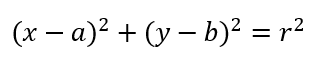
En este punto, cabe notar que si el centro es (0,0), entonces, la ecuación será la siguiente:
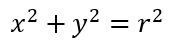
Lo anterior quiere decir, por ejemplo, que teniendo una circunferencia que pasa por el punto (-3,1) y sabiendo que su centro es el punto (0,1), se puede calcular su radio:
Otra forma de expresar la ecuación de una circunferencia es a través de una función paramétrica, donde debemos tener un ángulo α de referencia. Entonces, volviendo a considerar el centro C(a,b) y un punto cualquiera de la figura Q(x,y), se debe cumplir que:
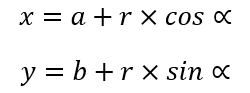
Por ejemplo, volviendo al ejemplo anterior, con C(-3,1) y Q(0,1)
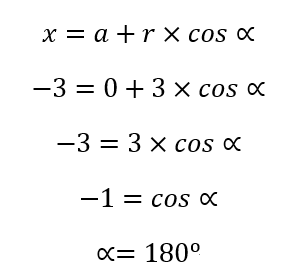
Luego, comprobamos en el eje vertical:
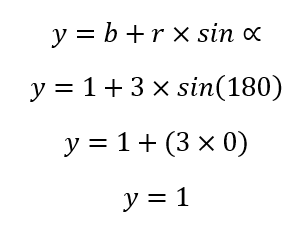
Es decir, en este caso, el ángulo de referencia α es 180 o π radianes.
Longitud de la circunferencia
La longitud (L) de la circunferencia es igual al radio (r) multiplicado por dos y por π o, lo que es lo mismo, el diámetro (D) multiplicado por π, como vemos en la siguiente fórmula:
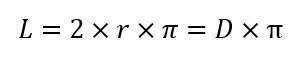
Entonces, si el radio de una circunferencia es 5 metros, por ejemplo, su longitud sería:
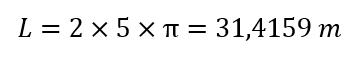
Área dentro de una circunferencia
Como precisamos previamente, el área dentro de la circunferencia (A) es un círculo, y su área puede calcularse con la siguiente fórmula, siendo r el radio y D el diámetro.
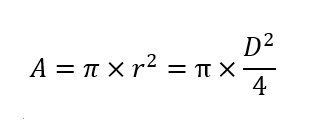
Continuando con el ejemplo anterior, el área de un círculo con una circunferencia de radio de 5 metros sería: