Área

Se suele usar en algunos casos indistintamente el término superficie o área, pero el primero se refiere al espacio, mientras que el segundo, a la medición del mismo. Es decir, el área es la medición de una superficie.

El área nos puede servir, en la práctica, para trabajar sobre ciertos espacios, por ejemplo, una hectárea de tierra agrícola. Sabiendo su área, sabremos cuánto podemos cosechar y, por ejemplo, cuánto requerirá de agua y fertilizante.

Lo explicado en este artículo es la definición de área desde el punto de vista geométrico. Sin embargo, es un término usado en otros ámbitos, por ejemplo, para hacer referencia a una rama de estudios o especialidad. Así, una persona puede decir: «No puedo dar una opinión sobre la legalidad de la nueva ley de alimentación saludable porque no es mi área».

El área de un polígono se calcula de distintos modos, según el número de lados, como veremos continuación con algunos ejemplos:

• Área de un triángulo: Existen dos formas generales para calcular el área de un triángulo. Primero, se puede multiplicar la base (que puede ser cualquiera de los lados) por la altura y dividir entre dos (debemos recordar que la altura es el segmento que une el vértice con su lado opuesto formando un ángulo de 90º).

Otra forma es con la fórmula de Herón, siendo a, b y c las medidas de los lados de un triángulo, y s es el semiperímetro:

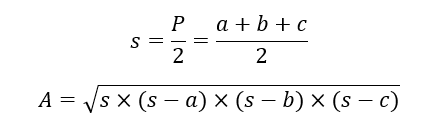
• Área de un cuadrado: Se eleva la cuadrado la longitud de cualquiera de los lados (L) de la figura (todos los lados son iguales).

• Área de un rectángulo: Se multiplican las longitudes de dos lados contiguos de la figura los cuales son distintos entre sí. Ancho por alto.

• Área de un rombo: Se multiplican las diagonales de la figura (diagonal mayor por diagonal menor) y se divide entre dos:

En general, el área de un cuadrilátero (polígono de cuatro lados), puede calcularse con la siguiente fórmula, siendo α el ángulo que se forma entre las dos diagonales como vemos en la figura de abajo:

Cabe precisar que se puede utilizar cualquiera de los ángulos señalados en la figura porque α es igual a γ, mientras que β es igual a δ (por propiedad al ser opuestos). Asimismo, α y β (al igual que γ con δ) son suplementarios, es decir, suman 180º, y el seno de dos ángulos suplementarios es el mismo.

Entonces, por ejemplo, si tenemos un cuadrilátero con dos diagonales que miden 5,7 y 5,8 metros, y forman entre sí un ángulo de 104º. ¿Cuál es el área de la figura?

El área de un círculo puede calcularse con la siguiente fórmula:

Entonces, supongamos que sabemos que un círculo tiene un diámetro de 20 metros. ¿Cuál sería su área? Recordemos primero que el diámetro es el doble del radio: