Definición de poliedros
 Los poliedros son elementos geométricos que disponen de caras planas y que albergan un volumen que no es infinito. Las raíces etimológicas del término, que se hallan en la lengua griega, refieren a “muchas caras”.
Los poliedros son elementos geométricos que disponen de caras planas y que albergan un volumen que no es infinito. Las raíces etimológicas del término, que se hallan en la lengua griega, refieren a “muchas caras”.
Un poliedro puede ser entendido como un cuerpo sólido y tridimensional. Cuando todas sus caras y ángulos son iguales entre sí, se lo califica como un poliedro regular. De lo contrario, será un poliedro irregular.
Otra clasificación posible está vinculada a la cantidad de caras que presenta. Un poliedro de seis caras recibe el nombre de hexaedro, un poliedro de cinco caras se conoce como pentaedro y así sucesivamente, formando siempre la denominación con el prefijo griego correspondiente (hexa, penta, tetra, etc.).
Por otra parte, se puede diferenciar entre poliedros cóncavos y poliedros convexos. Los poliedros cóncavos son aquellos que, al unir dos puntos situados dentro del cuerpo, el segmento correspondiente sale de la superficie. En cambio, en los poliedros convexos, los segmentos que vinculan dos puntos del espacio interior nunca salen del cuerpo geométrico.
Un ejemplo de poliedro es el cubo, un poliedro regular de cuatro caras iguales, cuyos ángulos interiores son congruentes entre sí. Esto quiere decir que los dados construidos de esta manera son poliedros. Las cajas cuyas caras son cuadrados también ingresan dentro del grupo de los poliedros.
Otro ejemplo de poliedro son los prismas: en este caso, se trata de poliedros irregulares. Es importante resaltar que las clasificaciones no siempre son excluyentes. El prisma es un poliedro irregular pero, a su vez, es un poliedro convexo.
Los poliedros se clasifican en diversas familias, dos de las cuales se listan a continuación:
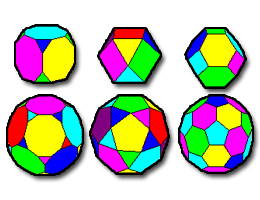
* sólidos platónicos: se trata de aquéllos que tienen caras y ángulos iguales y que son convexos. Tan sólo hay cinco poliedros de esta familia, que son el cubo, el dodecaedro, el tetraedro, el octaedro y el icosaedro. Esta familia resulta esencial, ya que de ella derivan otras, como los sólidos arquimedianos;
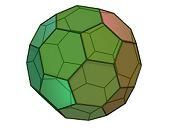
 * sólidos arquimedianos: son convexos, sus vértices son uniformes y sus caras, regulares (pero no uniformes). Existen tan sólo once, y algunos de ellos se consiguen truncando los platónicos, o sea cortando sus vértices o sus aristas. Algunos de los sólidos arquimedianos son el cubo truncado, el rombicuboctaedro, el rombicosidodecaedro y el icosidodecaedro truncado;
* sólidos arquimedianos: son convexos, sus vértices son uniformes y sus caras, regulares (pero no uniformes). Existen tan sólo once, y algunos de ellos se consiguen truncando los platónicos, o sea cortando sus vértices o sus aristas. Algunos de los sólidos arquimedianos son el cubo truncado, el rombicuboctaedro, el rombicosidodecaedro y el icosidodecaedro truncado;
Se conoce con el nombre de poliedro dual a aquél cuyos vértices son correspondientes al centro de las caras de un segundo poliedro. Veamos algunos datos curiosos: el poliedro dual de uno dual se parece al original; el dual de uno con vértices equivalentes también tiene caras equivalentes; el de un poliedro que tiene aristas equivalentes, también las tendrá equivalentes. Se asocian a esta clasificación los sólidos de Kepler-Poinsot y los platónicos, entre otros poliedros regulares.
Si bien se pueden reconocer varias clases de dualidad desde las cuales relacionar dos figuras, entre las más usadas se encuentran la reciprocidad polar y la dualidad topológica. Veamos a continuación la definición de estos conceptos:
* reciprocidad polar: por lo general, para definir la dualidad hablando de su reciprocidad polar se toma como referencia una esfera concéntrica, de manera que cada polo (o vértice) se asocie a una cara y a su plano (denominado polar), de forma tal que la recta imaginaria que pasa por el vértice y el centro sea perpendicular a dicho plano y se pueda obtener el cuadrado del radio si se efectúa el producto de las distancias desde cada lado hasta el centro;
* dualidad topológica: cuando se distorsiona un poliedro dual de manera que ya no se puede obtener por reciprocidad, se puede decir que el original y el actual son topológicamente duales, pero no recíprocos polares.
