Definición de hipérbola
El vocablo griego hyperbolḗ llegó al latín como hyperbŏla. A nuestro idioma el concepto arribó como hipérbola, un término que se emplea en el terreno de la geometría.
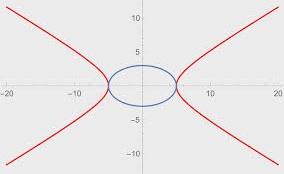 Se denomina hipérbola a la curva con dos focos que resulta simétrica respecto a un par de ejes perpendiculares entre sí. Para trazar una hipérbola, se corta un cono recto con un plano, generando un ángulo menor que aquel que forma la generatriz respecto al eje de revolución.
Se denomina hipérbola a la curva con dos focos que resulta simétrica respecto a un par de ejes perpendiculares entre sí. Para trazar una hipérbola, se corta un cono recto con un plano, generando un ángulo menor que aquel que forma la generatriz respecto al eje de revolución.
Una hipérbola presenta dos ramas abiertas. Ambas se dirigen en sentidos opuestos, aproximándose de forma indefinida a dos asíntotas. Esto hace que, considerando dos puntos fijos, la diferencia de sus distancias sea constante.
Una definición formal indica que considerados dos puntos (F1 y F2) que se denominan focos, la hipérbola es el conjunto de los puntos del plano en los cuales el valor absoluto que se registra al considerar la diferencia de sus distancias a los focos (los mencionados F1 y F2) es constante.
Además de los focos, en la hipérbola es posible reconocer otros elementos. Entre ellos aparecen el eje focal (la recta que pasa por ambos focos), el eje secundario (la mediatriz que une el segmento que va de un foco a otro), el centro (el punto de intersección de estos ejes) y los vértices.
De acuerdo a la menor o mayor abertura de las ramas de la hipérbola, se calcula su excentricidad. Esta excentricidad se conoce dividiendo la mitad de la distancia del eje focal por la mitad de la distancia del eje mayor.
