Definición de curva normal
Antes de entrar de lleno en el significado del término curva normal, se hace necesario proceder a descubrir el origen etimológico de las dos palabras que le dan forma:
-Curva es una palabra que deriva del latín, exactamente de “curvus” que puede traducirse como “curvado”.
-Normal, por otro lado, también procede del latín. En su caso, es fruto de la suma de dos componentes perfectamente delimitados: el sustantivo “norma”, que es sinónimo de “regla” o “modelo”, y el sufijo “-al”, que se utiliza para indicar “pertenencia” o “relación”.
Una curva es aquello que se aparta de forma continua de la dirección recta, aunque sin crear ángulos. También se llama curva a la línea empleada para representar, de forma gráfica, la magnitud de un fenómeno de acuerdo a los valores de una de sus variables. Normal, por su parte, es lo que resulta natural o que funciona como norma.
 Estas ideas pueden ayudarnos a entender qué es una curva normal, aunque el concepto tiene un uso específico en el terreno de la estadística. Se llama curva normal a la distribución gaussiana: la distribución de probabilidad de una variable continua que suele resultar próxima a un fenómeno real.
Estas ideas pueden ayudarnos a entender qué es una curva normal, aunque el concepto tiene un uso específico en el terreno de la estadística. Se llama curva normal a la distribución gaussiana: la distribución de probabilidad de una variable continua que suele resultar próxima a un fenómeno real.
La utilización de un modelo normal permite asumir que las observaciones derivan de la sumatoria de causas independientes. La curva normal, en este marco, sirve para modelar fenómenos sociales y naturales de forma aproximada a la realidad.
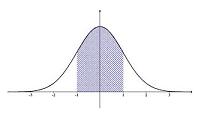
La representación gráfica de la curva normal se conoce como campana de Gauss. Esta línea de forma acampanada resulta simétrica respecto a un cierto parámetro: hay una zona media cóncava, que tiene en el centro el valor medio de la función, y dos extremos convexos que tienden a acercarse al eje X. La distribución gaussiana, por lo tanto, muestra los valores más frecuentes en el centro de la campana, quedando los menos frecuentes en los extremos.
Tomemos el caso de la altura promedio de los hombres de entre 18 y 60 años nacidos en una cierta región. Aunque en dicho conjunto hay personas que miden 1,45 metros y otras que miden 2,05 metros, la mayoría de los sujetos tienen una altura de entre 1,65 y 1,85 metros. La curva normal hará que estos valores más comunes se reflejen en el centro de la campana de Gauss.
De la misma manera, además de todo lo expuesto, no podemos pasar por alto tampoco que hay otra serie de aspectos relevantes sobre la curva normal que merece la pena conocer. Nos estamos refiriendo a los siguientes:
-Permite no solo “modelar” lo que son fenómenos sociales o naturales sino también otros de tipo psicológico.
-En el siglo XVIII es donde se encuentra el origen de la curva o distribución normal. En concreto, apareció en el año 1733 en un artículo escrito por el matemático francés Abraham de Moivre, que se ha convertido en un referente de la estadística por las aportaciones que realizó sobre la teoría de la probabilidad. No obstante, tras él la perfeccionarían otras figuras como sería el caso de Adrien-Maire Legendre o Johann Carl Friedrich Gauss.
-Su nombre como tal le fue dado años más tarde. En concreto se le otorgó en 1875 de la mano de personajes como Francis Galton, Charles S. Peirce y Wilhem Lexis.
