Definición de corolario
 Del latín corollarium, corolario es una proposición que se deduce de lo demostrado con anterioridad, por lo que no requiere de una prueba particular. Se entiende que un corolario es una conclusión obvia o inevitable que se desprende de ciertos antecedentes.
Del latín corollarium, corolario es una proposición que se deduce de lo demostrado con anterioridad, por lo que no requiere de una prueba particular. Se entiende que un corolario es una conclusión obvia o inevitable que se desprende de ciertos antecedentes.
Por ejemplo: “El corolario de fumar tres paquetes de cigarillos al día es una enfermedad pulmonar”, “El descenso del equipo es el corolario de varios años de mala gestión dirigencial”, “La renuncia del senador tras el escándalo no es otra cosa que el corolario de la situación que estalló el pasado miércoles”, “El corolario no podía ser diferente: los tres manifestantes fueron liberados por falta de mérito”.
En el lenguaje cotidiano, un corolario aparece como algo lógico o ineludible si se tienen en cuenta los hechos precedentes. Un jugador de fútbol discute con el director técnico de su equipo durante un entrenamiento. Al día siguiente, critica públicamente al entrenador. Al tercer día, se ausenta sin aviso de la práctica del equipo. El corolario de esta situación es que el entrenador desafecte al jugador del plantel y deje de tenerlo en cuenta.
En el ámbito de la lógica y de la matemática, el corolario es la evidencia de un teorema ya demostrado, sin la necesidad de seguir invirtiendo esfuerzos en su demostración. Si se afirma que todos los ángulos interiores de un cuadrado son ángulos rectos (90º) y que todos los cuadrados tienen cuatro ángulos interiores, un corolario de dichas afirmaciones es que los ángulos interiores de un cuadrado suman 360º.
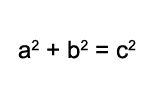 Del conocido Teorema de Pitágoras, el cual expone que la suma de los cuadrados de los catetos de un triángulo rectángulo devuelven el mismo valor que elevar la hipotenusa al cuadrado, también se desprende un corolario, el cual varía según se esté hablando de números pares o impares. Para desarrollar este corolario, es necesario primero establecer la fórmula del teorema como se aprecia en la imagen.
Del conocido Teorema de Pitágoras, el cual expone que la suma de los cuadrados de los catetos de un triángulo rectángulo devuelven el mismo valor que elevar la hipotenusa al cuadrado, también se desprende un corolario, el cual varía según se esté hablando de números pares o impares. Para desarrollar este corolario, es necesario primero establecer la fórmula del teorema como se aprecia en la imagen.
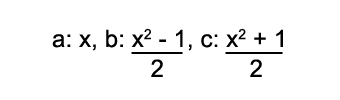
Aquí se puede apreciar que los dos catetos están representados por las variables a y b, y que la c corresponde a la hipotenusa. Basados en esta definición, si tenemos un número x impar, dicho trío pitagórico se podrá obtener a través de los cálculos que se muestran en la imagen.
A la variable a se le asigna el valor de x; a b le corresponde x elevado al cuadrado, menos 1, todo dividido por 2; a c, similar a b pero sumando 1 al cuadrado en lugar de restarlo. Habiendo entendido dicho desarrollo, es posible elevar cada componente al cuadrado y ubicarlos en la igualdad antes mencionada.
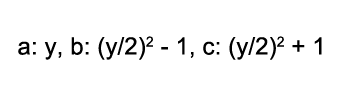 Con respecto a los números pares, si tomamos por ejemplo un número y, el trío pitagórico se deberá formar como se ve en la imagen. En este caso, a recibe el valor de y; a b se le asigna el cuadrado del resultado de y sobre 2, todo menos 1; el valor de c es similar a b, pero sumando 1 al cuadrado anterior. Con todo esto, nuevamente estamos en condiciones de definir la igualdad que permite comprobar el Teorema de Pitágoras.
Con respecto a los números pares, si tomamos por ejemplo un número y, el trío pitagórico se deberá formar como se ve en la imagen. En este caso, a recibe el valor de y; a b se le asigna el cuadrado del resultado de y sobre 2, todo menos 1; el valor de c es similar a b, pero sumando 1 al cuadrado anterior. Con todo esto, nuevamente estamos en condiciones de definir la igualdad que permite comprobar el Teorema de Pitágoras.
El matemático Tales de Mileto, oriundo de Grecia y nacido en el siglo VI a.C., legó dos importantes teoremas a la geometría, cada uno con sus respectivos corolarios. El primero de los teoremas establece que si se traza una línea paralela a alguno de los lados de un triángulo, la figura resultante será otro triángulo, similar al primero. Su corolario es la deducción de que la proporción de los lados del nuevo triángulo también es equivalente a la de los originales.
El segundo de los teoremas de Tales explica que si en una circunferencia de diámetro AC escogemos un punto cualquiera, diferente de A y C, entonces los tres formarán un triángulo rectángulo. De aquí se desprenden dos corolarios:
1) dado que la distancia entre el centro de la circunferencia y cualquiera de los tres puntos del triángulo es la misma, entonces la mediana de la hipotenusa (segmento entre el centro y el punto B) siempre medirá la mitad de la hipotenusa;
2) similar al primero, el radio de la circunferencia equivale a la mitad de la hipotenusa, y el circuncentro se ubica siempre en su punto medio.
