Sistema octal: concepto, sistema de numeración, ejemplos
¿Qué es un sistema octal?
El sistema octal es un sistema de numeración posicional de base ocho (8); es decir, que consta de ocho dígitos, que son: 0, 1, 2, 3, 4, 5, 6 y 7. Por lo tanto, cada dígito de un número octal puede tener cualquier valor de 0 a 7. Los números octales son formados a partir de los números binarios.
Esto es así porque su base es una potencia exacta de dos (2). Es decir, los números que pertenecen al sistema octal se forman cuando estos son agrupados en tres dígitos consecutivos, ordenados de derecha a izquierda, obteniendo de esa forma su valor decimal.
Historia del sistema octal
El sistema octal tiene su origen en la antigüedad, cuando las personas usaban sus manos para contar de ocho en ocho los animales.
Por ejemplo, para contar el número de vacas en un establo se comenzaba a contar con la mano derecha, juntando el dedo pulgar con el meñique; luego para contar el segundo animal se juntaba el pulgar con el dedo índice, y así sucesivamente con los dedos restantes de cada mano, hasta completar 8.
Existe la posibilidad de que en la antigüedad se usara el sistema de numeración octal antes que el decimal para poder contar los espacios interdigitales; es decir, contar todos los dedos a excepción de los pulgares.
Posteriormente se estableció el sistema de numeración octal, que se originó a partir del sistema binario, porque este necesita de muchos dígitos para representar solo un número; a partir de entonces se crearon los sistemas octales y hexagonales, que no requieren de tantos dígitos y que fácilmente pueden convertirse al sistema binario.
Sistema de numeración octal
El sistema octal está formado por ocho dígitos que van del 0 al 7. Estos tienen el mismo valor que en el caso del sistema decimal, pero su valor relativo cambia dependiendo de la posición que estos ocupen. El valor de cada posición es dado por las potencias de base 8.
Las posiciones de los dígitos en un número octal tienen los siguientes pesos:
84, 83, 82, 81, 80, punto octal, 8-1, 8-2, 8-3, 8-4, 8-5.
El dígito octal mayor es 7; de esa manera, cuando se cuenta en este sistema se va aumentando una posición de un dígito de 0 a 7. Cuando se llega a 7 se recicla a 0 para el siguiente conteo; de esa forma se incrementa la siguiente posición del dígito. Por ejemplo, para contar secuencias, en el sistema octal será:
- 0, 1, 2, 3, 4, 5, 6, 7, 10.
- 53, 54, 55, 56, 57, 60.
- 375, 376, 377, 400.
Existe un teorema fundamental que es aplicado al sistema octal, y es expresado de la siguiente manera:
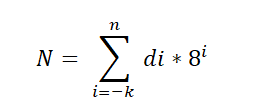
En esta expresión di representa al dígito multiplicado por la potencia de base 8, que indica el valor posicional de cada dígito, de la misma forma en la que se ordena en el sistema decimal.
Por ejemplo, se tiene el número 543,2. Para llevarlo al sistema octal se descompone de la siguiente manera:
N = ∑ [(5 * 82) + (4 * 81) + (3 *80) + (2 *8-1)] = (5 * 64) +(4 * 8) + (2*1) + (2 * 0,125)
N = 320 +32 + 2 + 0,25 = 354 + 0,25d
De esa forma se tiene que 543,2q = 354,25d. El subíndice q indica que se trata de un número octal que también puede ser representado por el número 8; y el subíndice d hace referencia al número decimal, que también puede representarse con el número 10.
Conversión del sistema octal al decimal
Para convertir un número del sistema octal a su equivalente en el sistema decimal solo se tiene que multiplicar cada dígito octal por su valor posicional, comenzando desde la derecha.
Ejemplo 1
7328 = (7* 82) + (3* 81) + (2* 80) = (7 * 64) + (3 * 8) + (2 * 1)
7328= 448 +24 +2
7328= 47410
Ejemplo 2
26,98 = (2 *81) + (6* 80) + (9* 8-1) = (2 * 8) + (6 * 1) + (9 * 0,125)
26,98 = 16 + 6 + 1,125
26,98= 23,12510
Conversión del sistema decimal al octal
Un número entero decimal puede ser convertido en un número octal utilizando el método de la división repetida, donde el entero decimal se divide entre 8 hasta que el cociente sea igual a 0, y los residuos de cada división van a representar al número octal.
Los residuos son ordenados del último al primero; es decir, que el primer residuo será el dígito menos significativo del número octal. De esa forma, el dígito más significativo será el último residuo.
Ejemplo
Octal del número decimal 26610
– Se divide el número decimal 266 entre 8 = 266/8 = 33 + residuo de 2.
– Luego se divide el 33 entre 8 = 33/8 = 4 + residuo de 1.
– Se divide 4 entre 8 = 4/8 = 0 + residuo de 4.
Como con la última división se obtiene un cociente menor a 1, quiere decir que el resultado ha sido encontrado; solo se tienen que ordenar los restos de forma inversa, de tal forma que el número octal del decimal 266 es 412, como se puede observar en la siguiente imagen:

Conversión del sistema octal al binario
La conversión del sistema octal al binario se lleva a cabo al convertir el dígito octal a su dígito binario equivalente, formado por tres dígitos. Existe una tabla que muestra cómo se convierten los ocho posibles dígitos:
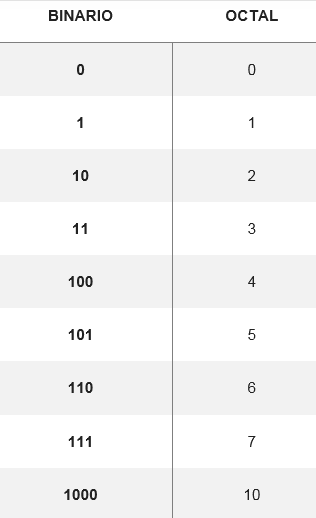
A partir de esas conversiones se puede cambiar cualquier número del sistema octal al binario, como por ejemplo, para convertir el número 5728 se buscan sus equivalentes en la tabla. Así, se tiene que:
58 = 101
78=111
28 = 10
Por lo tanto, 5728 equivale en el sistema binario a 10111110.
Conversión del sistema binario al octal
El proceso de conversión de números enteros binarios a números enteros octales es la operación inversa al proceso anterior.
Es decir, se agrupan los bits del número binario en dos grupos de tres bits, comenzando de derecha a izquierda. Luego, se hace la conversión de binario a octal con la tabla anterior.
En algunos casos el número binario no tendrá grupos de 3 bits; para completarlo, se agregan uno o dos ceros a la izquierda del primer grupo.
Por ejemplo, para cambiar el número binario 11010110 a octal se realiza lo siguiente:
– Se forman grupos de 3 bits comenzando por la derecha (último bit):
11010110
– Como el primer grupo está incompleto, se agrega un cero a la izquierda:
011010110
– Se hace la conversión a partir de la tabla:
011 = 3
010 = 2
110 = 6
De esa forma, el número binario 011010110 equivale a 3268.
Conversión del sistema octal al hexadecimal y viceversa
Para hacer el cambio de un número octal al sistema hexadecimal o de hexadecimal a octal, es necesario que primero se convierta el número en binario, y luego al sistema que se desee.
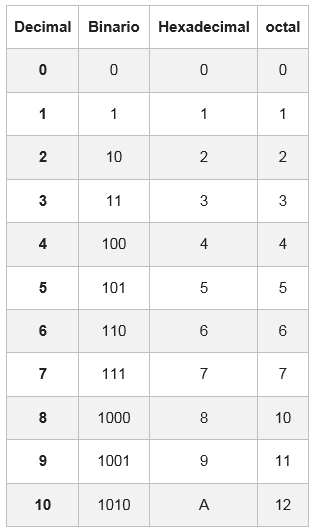
Para ello existe una tabla donde se representa cada dígito hexadecimal con su equivalencia en el sistema binario, compuesto por cuatro dígitos.
En algunos casos, el número binario no tendrá grupos de 4 bits; para completarlo, se agregan uno o dos ceros a la izquierda del primer grupo
Ejemplo
Convertir el número octal 1646 en un número hexadecimal:
– Se convierte el número de octal a binario
18 = 1
68 = 110
48 = 100
68 = 110
– Así, 16468 = 1110100110.
– Para convertir de binario a hexadecimal primero se ordenan en grupo de 4 bits, empezando de derecha hacia izquierda:
11 1010 0110
– Se completa con ceros el primer grupo, para que este pueda tener 4 bits:
0011 1010 0110
– Se hace la conversión del sistema binario al hexadecimal. Se sustituyen las equivalencias por medio de la tabla:
0011 = 3
1010 = A
0110 = 6
De esa forma, el número octal 1646 equivale a 3A6 en el sistema hexadecimal.
