Función creciente: cómo identificarla, ejemplos, ejercicios

Se tiene una función creciente cuando el valor de y aumenta si el de x también aumenta, en contraposición a las funciones decrecientes, en las cuales el valor de y disminuye cuando el de x aumenta.

La siguiente figura muestra una función creciente, y se observa claramente que al desplazarse de izquierda a derecha sobre el eje x, el valor de la respectiva coordenada y, equivalente a f(x), va aumentando paulatinamente. Se dice que si para todo x₂ > x₁, entonces existe y₂ > y₁.

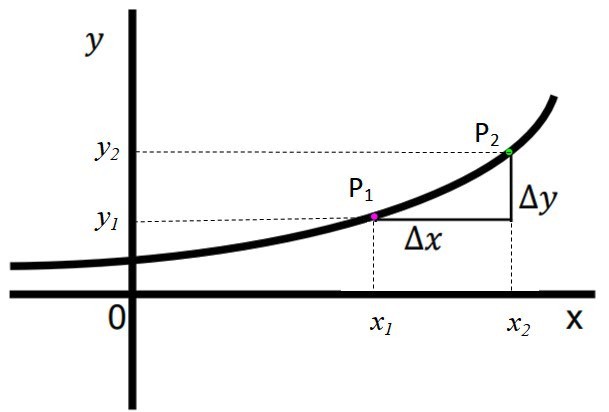
Los puntos P₁ y P₂ que se muestran, tienen respectivamente, coordenadas (x₁, y₁) y (x₂,y₂). Se definen:

Δy = y₂ –y₁

Δx = x₂ –x₁

En esta función, tanto Δy como Δx tienen signo positivo, lo cual significa que y₂ > y₁ y x₂ > x₁, respectivamente. Esta es una clara señal de que la función efectivamente crece.

Un buen ejemplo de función siempre creciente (monótona creciente) es el logaritmo neperiano de un número real. Cuanto mayor el número, más grande es su logaritmo.

Índice del artículo

• 1 ¿Cómo identificar una función creciente?
  • 1.1 Criterio de la primera derivada
• 2 Ejemplos de funciones crecientes
  • 2.1 Peso en función de la edad
  • 2.2 La función logaritmo
  • 2.3 La función raíz cuadrada de un número real
  • 2.4 La función afín y la función lineal
  • 2.5 La función exponencial
  • 2.6 La función potencial de índice impar
• 3 Ejercicios
  • 3.1 Ejercicio 1
  • 3.2 Ejercicio 2
• 4 Referencias

¿Cómo identificar una función creciente?

En una función simple y continua como la mostrada en la figura 1, es fácil determinar si la función es creciente o decreciente, siempre que se disponga de la gráfica.

Sin embargo, funciones más complejas pueden crecer en algunos intervalos y decrecer en otros. Por eso se habla de intervalos de crecimientoy decrecimiento de una función.

En la red hay graficadoras online gratuitas, como por ejemplo Geogebra, que permiten graficar todo tipo de funciones. Teniendo la gráfica, es fácil determinar si la función es siempre creciente, como f(x) = log x o si tiene intervalos en los que crece y otros en los que decrece y cuáles son.

Criterio de la primera derivada

Considerando un cierto intervalo numérico I, si el cociente entre las cantidades Δy y Δx es positivo, la función es creciente. Y por el contrario, si es negativo, la función es decreciente.

Se tiene entonces que:

Δy / Δx > 0 → Función creciente

El hecho de que Δy / Δx > 0 y la función es creciente en un determinado intervalo, sugiere que la primera derivada de la función, o más bien su signo, puede usarse como un criterio para determinar si en efecto, la función crece en un intervalo particular o incluso en un cierto punto de su dominio.

En efecto, la primera derivada se define como la pendiente de la curva cada punto:

El siguiente teorema ofrece un criterio para conocer cuándo una función es creciente en el intervalo (a,b):

Teorema

Sea f (x) una función derivable en (a,b). Si f´(x) > 0, para todo valor de x perteneciente a dicho intervalo, se dice que f(x) es creciente en (a,b).

El teorema se aplica para averiguar en qué intervalos la función crece, siguiendo estos pasos:

Paso 1

Hallar los puntos en los que f´(x) = 0, así como aquellos en los que f´(x) no existe. Estos, llamados puntos críticos, son puntos en los que f´(x) puede cambiar de signo y por lo tanto f(x) tiene oportunidad de pasar de creciente a decreciente o viceversa.

Paso 2

Hallar el signo de f´(x) para un valor arbitrario en cada uno de los intervalos determinados por los puntos hallados en el paso 1.

Paso 3

Usar el teorema para saber si la función es creciente o no en cada intervalo.

Ejemplos de funciones crecientes

Hay funciones que tienen algunos intervalos de crecimiento y otros de decrecimiento, pero las que se muestran a continuación son siempre crecientes.

Peso en función de la edad

El peso de la persona desde que nace, hasta aproximadamente finalizar la adolescencia, es casi siempre una función creciente de la edad. Bebés y niños crecen y se desarrollan con los años, y luego, al llegar a la adultez, se espera que mantengan un peso estable el resto de su vida, aunque los altibajos son muy frecuentes.

La función logaritmo

Las funciones de variable real logaritmo neperiano f(x) = ln x y logaritmo decimal f(x) = log x siempre son crecientes.

La función raíz cuadrada de un número real

Otra función que siempre es creciente es la función raíz cuadrada de un número real positivo:

y = √x

La función afín y la función lineal

La función afín:

f (x) = mx + b

Es creciente siempre que la recta sea de pendiente positiva. De igual manera, las funciones identidad y lineal:

f (x) = x  y  f(x) = ax, con a >0

Son crecientes en todo su dominio.

La función exponencial

Una función exponencial como f(x) = e^x  y en general, la función de la forma:

f (x) = a^x, con a>1

Son crecientes en todo su dominio.

La función potencial de índice impar

Las funciones potenciales de exponente impar, como estas:

• f (x) = x³
• g (x) = x⁵

Son siempre crecientes.

Ejercicios

Ejercicio 1

Determinar en qué intervalos la función representada en la siguiente gráfica es creciente:

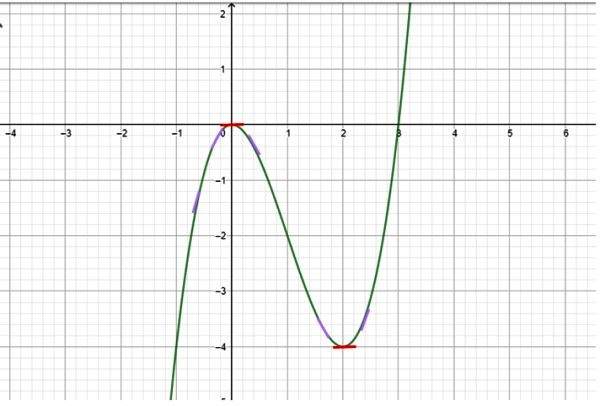
Solución

Como se dispone de la gráfica, a partir de su observación cuidadosa se determina que la función tiene el siguiente comportamiento:

-Desde x → -∞ hasta x = 0 la función es creciente, ya que los valores de y se hacen cada vez menos negativos. Se han dibujado pequeños segmentos de recta en color morado para señalar la pendiente de la recta tangente a la curva en varios puntos (la pendiente de la recta tangente a la curva es precisamente su primera derivada).

Estos segmentos tienen pendiente positiva, por lo que el teorema asegura que la función es creciente en este intervalo.

-Pero en x = 0 la pendiente de la curva se anula, lo que se indica con un pequeño segmento rojo horizontal. Este es un punto crítico de la función.

A partir de allí la función comienza a decrecer, haciéndose cada  vez más negativos los valores de y. Esta situación prosigue hasta que x = 2, que es otro punto crítico.

Luego, en el intervalo desde x = 0 hasta x = 2 la función decrece.

-A partir de x=2 la función se hace cada vez menos negativa, hasta que en x = 3 cruza al eje x y sigue haciéndose más positiva cada vez. Por lo tanto este es un intervalo de crecimiento.

Conclusión: los intervalos de crecimiento son (-∞,0) y (2, ∞+), mientra que el intervalo de decrecimiento es (0,2).

Ejercicio 2

Determinar los intervalos de crecimiento de la siguiente función, mediante el criterio de la primera derivada:

f(x) = x² – 2x

Solución

Siguiendo los pasos indicados anteriormente, se calcula la primera derivada y se iguala a 0 para hallar los puntos críticos:

f’(x) = 2x -2

2x – 2 = 0

x = 1

Este valor determina la existencia de los intervalos (-∞, 1) y (1, ∞+). Se eligen dos valores arbitrarios que pertenezcan a cada uno:

-Para x = 0, que pertenece a  (-∞, 1), se tiene que f’(0) = 2.0 – 2 = -2. Como el resultado es negativo, la función es decreciente en este intervalo.

-Para x = 3, perteneciente a (1, ∞+), la primera derivada vale f’(3) = 2.3 – 2 = 4. Dado que el resultado es positivo, se concluye que la función crece en este intervalo.

El lector puede graficar la función original f(x) = x² – 2x en una graficadora online para corroborar este resultado.

Referencias

1. Ayres, F. 2000. Cálculo. 5ed. Mc Graw Hill.
2. Leithold, L. 1992. Cálculo con Geometría Analítica. HARLA, S.A.
3. Purcell, E. J., Varberg, D., & Rigdon, S. E. (2007). Cálculo. México: Pearson Educación.
4. Matemóvil. Funciones, crecientes, decrecientes y constantes. Recuperado de: matemovil.com
5. Requena, B. Funciones crecientes. Recuperado de: universoformulas.com.
6. Stewart, J. 2006. Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.