¿Cuántos milésimos caben en un décimo? Ejemplos, ejercicios
En un décimo caben 100 milésimos y para quedar convencidos, es necesario considerar que la unidad se puede dividir en 10, 100, 1000 o más partes iguales, lo cual resulta conveniente, pues manejar fracciones con estos denominadores es particularmente fácil.
Lo primero es establecer el significado de los términos décimos, centésimos y milésimos:
- Si la unidad se divide en 10 partes iguales, una de ellas se denomina un décimo.
- Al dividir la unidad en 100 partes iguales, cada una es un centésimo.
- Por último, si se divide en 1000 partes iguales, una de ellas es un milésimo.
Se podría proseguir indefinidamente, dividiendo la unidad en partes iguales cada vez más pequeñas, como 10.000 por ejemplo, esto es un diezmilésimo, luego seguirían los cienmilésimos y así, pero por el momento basta con llegar a los milésimos.
En todo caso, cuanto mayor sea el número de partes en que se divide la unidad, más pequeña será cada una de ellas. Por eso, un décimo es mayor que un centésimo, y este a su vez es más grande que un milésimo y un diezmilésimo.
Con esto en mente, un único décimo contiene 10 centésimos, y este a su vez posee 10 milésimos. Como un décimo tiene 10 centésimos, y cada centésimo tiene 10 milésimos, se sigue que 1 décimo tiene 10×10 milésimos = 100 milésimos.
Fracciones decimales y números decimales
El uso de los décimos, centésimos, milésimos y más, es frecuente en el ámbito cotidiano. Por ejemplo, se emplean al medir longitudes con una cinta métrica o adquirir alimentos y bebidas, cuyos precios suelen venir expresados en tantos pesos, euros, dólares… por cada kilogramo, 100 gramos, litros o mililitros de producto.
Para todos estos menesteres normalmente se utiliza el sistema métrico decimal. Este sistema de medidas es aceptado universalmente y se basa en potencias de 10. Esto significa que cada una de las unidades que lo componen, se relaciona con las demás en potencias de 10.
Al dividir la unidad entre potencias de 10, como se explicó al comienzo, surgen las siguientes fracciones decimales y su correspondiente expresión en números decimales:
- Décimas: 1/10 = 0.1
- Centésimas: 1/100 = 0.01
- Milésimas = 1 / 1000 = 0.001
- Diezmilésimas = 1 / 10.000 = 0.0001
- Cienmilésimas = 1/ 100.000 = 0.00001
- Millonésimas = 1 / 1.000.000 = 0.000001
Naturalmente, se puede dividir cualquier otro número diferente de 1, entre las potencias de 10 y obtener fracciones decimales. Es muy sencillo hacerlo, solamente hay que correr el punto decimal a la izquierda, tantos lugares como ceros tenga la potencia, por ejemplo:
- Dos décimas: 2/10 = 0.2
- Cinco centésimas: 5 / 100 = 0.05
- Ocho milésimas: 8 / 1000 = 0.008
Asimismo, un número decimal puede representarse a través de una fracción decimal, como sigue:
- 57.9 = 579 / 10
- 101.03 = 10103/100
Los números decimales se leen indicando primero la cantidad de unidades, luego las décimas, después las centésimas y así sucesivamente, por ejemplo, los números anteriores se leen del siguiente modo:
- 57.9 son 57 unidades y 9 décimas
- 101.03 equivalen a 101 unidades, 0 décimas y 3 centésimas
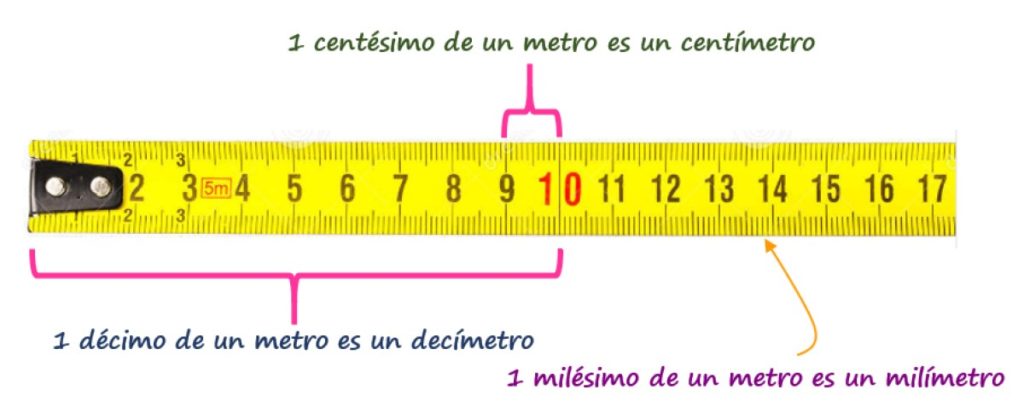
La cinta métrica
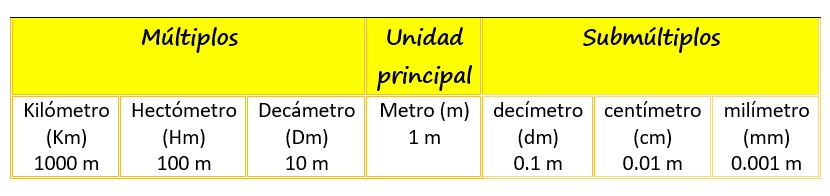
La cinta métrica se usa para medir longitudes y en ella se aplica el sistema métrico decimal. La unidad central es el metro y los principales múltiplos y submúltiplos se muestran en la siguiente tabla:
El décimo de un metro es el decímetro, por lo tanto:
1 m = 10 dm
A su vez, un metro tiene 100 cm, por lo que cada dm tiene 10 cm:
1 dm = 10 cm.
Por último, un metro tiene 1000 mm. Y ya que 1 cm = 10 mm, entonces 1 dm = 100 mm.
El metro es apropiado para medir la estatura de las personas, así como muebles y utensilios grandes y medianos. Los múltiplos como los kilómetros se usan frecuentemente para las distancias entre ciudades, largo de ríos, avenidas, autopistas, mientras que los submúltiplos como el centímetro se utilizan para medir ropa y utensilios pequeños.
Ejemplos
Ejemplo 1
En cada cantidad de la siguiente lista, hay un determinado número de milésimos equivalentes:
- En 5 unidades hay 5000 milésimos, ya que, de acuerdo a lo explicado anteriormente, 1 unidad = 1000 milésimos, por lo tanto 5 unidades = 5×1000 milésimos = 5000 milésimos.
- 12 centésimos tienen 12 × 10 milésimos = 120 milésimos, puesto que 1 centésimo = 10 milésimos.
- 40 décimos contienen 40 × 10 centésimos = 400 centésimos, y a su vez, como 1 centésimo tiene 10 milésimos, se puede ver que 400 × 10 = 4000 milésimos.
- 500 diezmilésimos equivalen a 500 / 10.000 = 0.05 unidades = 0.05 × 1000 = 50 milésimos.
Ejemplo 2
Las siguientes cantidades se pueden expresar como unidades, haciendo uso de los números decimales:
a) 46 centésimas, equivalen 0.46 unidades
b) 25.6 décimas, es igual a 0.256 unidades
c) 1091 milésimas, equivalen a 1.091 unidades, puesto que 1 unidad = 1000 milésimos.
d) 0.768 centésimas es lo mismo que 0.00768 unidades.
Ejercicios resueltos
Ejercicio 1
Escribir cuántos milésimos caben en:
a) 35 unidades
b) 9 décimas
c) 67 centésimas
Solución
a) 35 unidades = 2.35×1000 milésimos = 2350 milésimos
b) 9 décimas = 48.9 × 100 milésimos = 4890 milésimos
c) 67 centésimas = 976.67 × 10 milésimos = 9766.7 milésimos
Ejercicio 2
Escribir en forma de fracción:
a) 325 milésimos
b) 5 décimas
c) 22 centésimas
d) 5607 diezmilésimas
Solución
a) 325 milésimas = 325 / 1000
b) 5 décimas = 87.5/ 10 = 875/100
c) 22 centésimas = 22/100
d) 5607 diezmilésmas = 5607 /10.000
