Teselados: característica, tipos (regulares, irregulares), ejemplos
Los teselados son superficies recubiertas por una o más figuras llamadas teselas. Están por todos lados: en calles y edificaciones de todo tipo. Las teselas o baldosas son piezas planas, generalmente polígonos con copias congruentes o isométricas, las cuales se colocan siguiendo un patrón regular. De esta forma no quedan espacios sin ser cubiertos y las baldosas o mosaicos no se superponen.
En el caso que se emplee un solo tipo de mosaico formado por un polígono regular se tiene entonces un teselado regular, pero si se emplean dos o más tipos de polígonos regulares se trata entonces de un teselado semirregular.

Por último cuando los polígonos que forma el teselado no son regulares, entonces se trata de un teselado irregular.
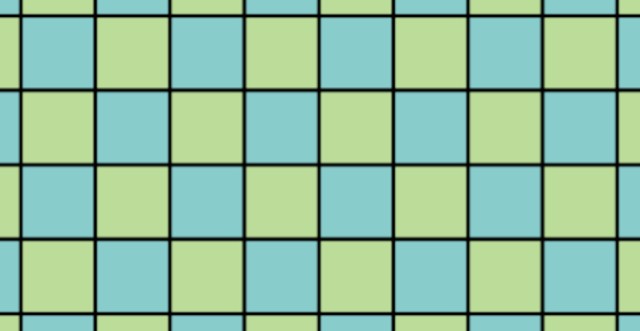
El tipo más común de teselado es el formado por mosaicos rectangulares y particularmente cuadrados. En la figura 1 tenemos un buen ejemplo.
Índice del artículo
- 1 Historia de los teselados
- 2 Teselados regulares
- 3 Teselados semirregulares
- 4 Teselados irregulares
- 5 Referencias
Desde hace miles de años se ha usado la teselación para cubrir pisos y paredes de los palacios y templos de diferentes culturas y religiones.
Por ejemplo, la civilización sumeria que floreció hacia el 3500 a.C. al sur de Mesopotamia, entre los ríos Éufrates y Tigris, usaron los teselados en su arquitectura.

Los teselados también han despertado el interés de los matemáticos de todas las épocas: comenzando por Arquímedes en el siglo III antes de Cristo, seguido por Johannes Kepler en 1619, Camille Jordan en 1880, hasta tiempos contemporáneos con Roger Penrose.
Penrose creó una teselación no periódica conocida como teselación de Penrose. Estos son apenas algunos nombres de científicos que aportaron mucho acerca de la teselación.
Los teselados regulares se hacen con un solo tipo de polígono regular. Por otra parte para que el teselado pueda considerarse regular todo punto del plano debe:
-Pertenecer al interior de polígono
-O bien a la arista de dos polígonos adyacentes
-Por último puede pertenecer al vértice común de al menos tres polígonos.
Con las restricciones anteriores se puede demostrar que solo los triángulos equiláteros, los cuadrados y los hexágonos pueden formar un teselado regular.
Hay una nomenclatura para denotar los teselados que consiste en enumerar en sentido de las agujas del reloj y separado por un punto, el número de lados de los polígonos que rodean cada nodo (o vértice) del teselado, siempre comenzando con el polígono de menor número de lados.
Esta nomenclatura se aplica a los teselados regulares y a los semirregulares.
La figura 3 muestra un teselado regular triangular. Debe notarse que cada nodo del teselado triangular es el vértice común de seis triángulos equiláteros.
La forma de denotar este tipo de teselado es 3.3.3.3.3.3, que también se denota por 36.

La figura 4 muestra un teselado regular compuesto únicamente por cuadrados. Debe notarse que cada nodo del teselado está rodeado por cuatro cuadrados congruentes. La notación que se aplica a este tipo de teselado cuadrado es: 4.4.4.4 o alternativamente 44
En un teselado hexagonal a cada nodo le rodean tres hexágonos regulares como se aprecia en la figura 5. La nomenclatura para un teselado hexagonal regular es 6.6.6 o alternativamente 63.

Los teselados semirregulares o teselados de Arquímedes consta de dos o más tipos de polígonos regulares. Cada nodo está rodeado por los tipos de polígonos que componen al teselado siempre en el mismo orden y se mantiene la condición de arista completamente compartida con el vecino.
Hay ocho teselaciones semirregulares:
- 3.6.3.6 (teselado tri-hexagonal)
- 3.3.3.3.6 (teselado hexagonal romo)
- 3.3.3.4.4 (teselado triangular elongado)
- 3.3.4.3.4 (teselado cuadrado romo)
- 3.4.6.4 (teselado rombi-tri-hexagonal)
- 4.8.8 (teselado cuadrado truncado)
- 3.12.12 (teselado hexagonal truncado)
- 4.6.12 (teselado tri-hexagonal truncado)
Algunos ejemplos de teselados semirregulares se muestran a continuación.
Es el que está compuesto por triángulos equiláteros y hexágonos regulares en la estructura 3.6.3.6, lo que significa que un nodo del teselado está rodeado (hasta completar una vuelta) por un triángulo, un hexágono, un triángulo y un hexágono. La figura 6 muestra un teselado de este tipo.

Al igual que el teselado del ejemplo anterior, este también consta de triángulos y hexágonos, pero su distribución en torno a un nodo es 3.3.3.3.6. La figura 7 ilustra claramente este tipo de teselado.

Es un teselado que consta de triángulos, cuadrados y hexágonos, en la configuración 3.4.6.4, el cual se muestra en la figura 8.

Se denominan teselados irregulares a aquellos que están formados por polígonos irregulares, o por polígonos regulares pero que no cumplen el criterio que un nodo es vértice de por lo menos tres polígonos.
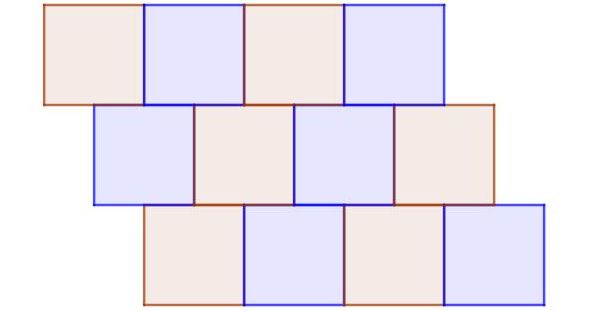
La figura 9 muestra un ejemplo de teselado irregular, en el que todos los polígonos son regulares y congruentes. Es irregular porque un nodo no es vértice común de al menos tres cuadrados y además hay cuadrados vecinos que no comparten completamente una arista.
El paralelogramo tesela una superficie plana, pero a menos que sea un cuadrado no puede formar un teselado regular.

Los hexágonos no-regulares con simetría central teselan una superficie plana, tal como lo muestra la siguiente figura:

Es una teselación muy interesante, compuesta por pentágonos con lados de igual longitud pero con ángulos desiguales, dos de los cuales son rectos y los otros tres tienen 120º cada uno.
Su nombre proviene de que este teselado se encuentra en el pavimento de algunas de las calles de El Cairo en Egipto. La figura 12 muestra el teselado de El Cairo.

El teselado durante en algunas partes de Andalucía y norte de África se caracterizan por la geometría y epigrafía, además de elementos ornamentales como la vegetación.
El teselado de palacios como el de la Alhambra se componían de alicatados formados por piezas de cerámica de muchos colores, con múltiples (por no decir infinitas) formas que desencadenaban en tramas geométricas.

Conocido también como tesellation, es una de las novedades con más auge en los videojuegos. Se trata de la creación de texturas para simular el teselado de los distintos escenarios que aparecen en el simulador.
Esto es el claro reflejo de que estas recubiertas siguen evolucionando traspasando las fronteras de la realidad.
- Disfruta las matemáticas. Teselaciones. Recuperado de: disfrutalasmatematicas.com
- Rubiños. Teselaciones ejemplos resueltos. Recuperado de: matematicasn.blogspot.com
- Weisstein, Eric W. «Demiregular tessellation». Weisstein, Eric W, ed. MathWorld. Wolfram Research.
- Wikipedia. Teselado. Recuperado de: es.wikipedia.com
- Wikipedia. Teselado regular. Recuperado de: es.wikipedia.com
