Pendiente de una recta: fórmula y ecuaciones, representación, ejemplos

La pendiente de una recta es la tangente del ángulo θ que dicha recta forma con el eje horizontal, que por convención se mide en sentido contrario al de las manecillas del reloj. La pendiente de cualquier recta siempre es constante y por eso es una de sus características más esenciales.

Para calcularla se necesita conocer dos puntos de la recta, cuyas coordenadas son (x₁,y₁) y (x₂,y₂). Entre ambos puntos se traza un segmento que pertenece a la recta y seguidamente se dibujan los segmentos que representan la distancia entre x₁ y x₂, y entre y₁ y y₂, como en la figura inferior.

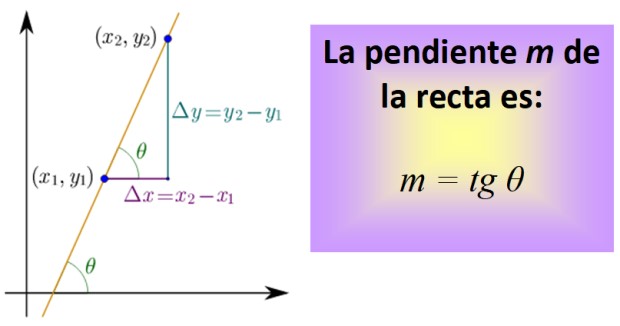
Los tres segmentos conforman un triángulo rectángulo cuyos catetos son: Δx = x₂ – x₁  y Δy = y₂ – y₁. Ellos corresponden respectivamente a un desplazamiento horizontal y a otro vertical.

Ahora se define un cociente, llamado tangente del ángulo θ y abreviado tg θ, que es precisamente la pendiente m de la recta:

m = tg θ = Δy / Δx

Nótese que para una recta, este ángulo permanece constante, independientemente de los puntos que se tomen para calcular su tangente. En todo caso, este valor nos ofrece una medida de cuán inclinada es la recta.

A través de las coordenadas de los puntos seleccionados, la fórmula para la pendiente queda:

m = ( y – y₁ ) / (x₂ – x₁)

Índice del artículo

• 1 Representación gráfica
• 2 Tipos de pendiente
• 3 ¿Cómo se calcula la pendiente una recta?
• 4 Ejercicios resueltos
  • 4.1 – Ejercicio 1
  • 4.2 – Ejercicio 2
• 5 Ejemplos
  • 5.1 Ejemplo 1
  • 5.2 Ejemplo 2
• 6 Referencias

Representación gráfica

A continuación tenemos varias situaciones en las cuales el concepto de pendiente es relevante. Su valor se puede calcular fácilmente midiendo el respectivo desplazamiento vertical y horizontal, y luego haciendo el cociente que se indicó al principio.

Esto nos da una idea del desnivel o el declive de alguna estructura, como por ejemplo una rampa, un tejado o una carretera:

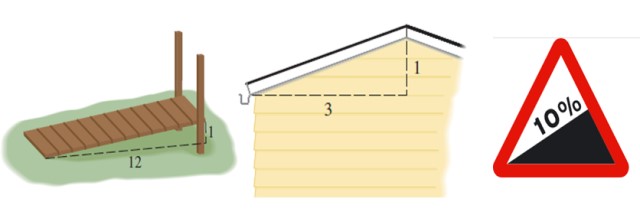
La pendiente de la rampa mostrada en la figura 2 a la izquierda es m= 1/12, la del tejado es m= 1/3 y la de la carretera está expresada en porcentaje. Un porcentaje de 10 % significa que por cada 100 metros que se avanza en sentido horizontal, se ganan 10 metros de altura:

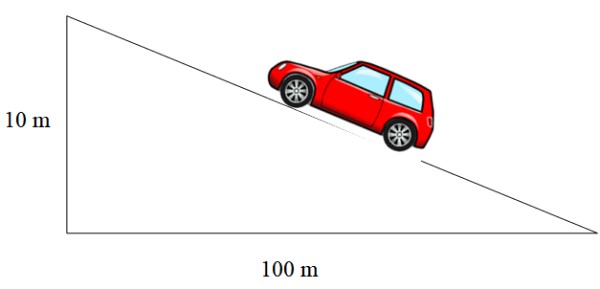
En tal caso la pendiente es 10/100 = 0.1, que expresada en porcentaje equivale al 10%.

Tipos de pendiente

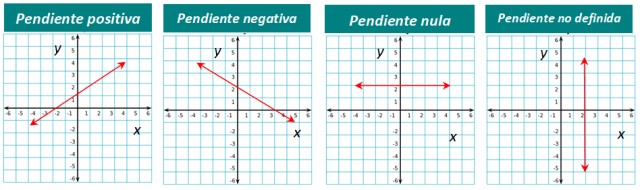
La pendiente de una recta puede ser positiva, negativa o nula. Por ejemplo la recta mostrada en la figura 1 tiene pendiente positiva. Lo apreciamos de inmediato porque vemos que la recta se “levanta” si la vemos de izquierda a derecha.

Si la recta desciende viéndola de izquierda a derecha, entonces su pendiente es negativa. Y cuando una recta es horizontal, su pendiente es nula.

Por último, para las rectas verticales, la pendiente no está definida.

La representación gráfica de cada tipo se encuentra a continuación:

¿Cómo se calcula la pendiente una recta?

Calcular la pendiente es muy sencillo, solamente hay que encontrar el desplazamiento vertical y el desplazamiento horizontal, y luego hacer el cociente entre ambos.

Cuando se tiene el dibujo de la recta en el plano cartesiano, estos desplazamientos se encuentran eligiendo dos puntos cualesquiera de la recta P₁ y P₂, determinando sus coordenadas y aplicando la definición dada al comienzo:

m = ( y – y₁ ) / (x₂ – x₁ )

Dado que el valor de la pendiente es independiente de la elección de P₁ y P₂ , vamos a escoger un punto P cualquiera de coordenadas (x,y) que pertenezca a la recta, cuyas coordenadas no son conocidas, y otro punto P₁ cuyas coordenadas sí lo sean: (x₁,y₁).

La pendiente es:

m = (y – y₁) / (x – x₁)

Podemos despejar la y:

y – y₁ = m (x – x₁)

Ahora supongamos que el punto P₁ es la intersección de la recta con el eje vertical, de coordenadas (0,b). Sustituyendo esto en la ecuación anterior:

y – b = m (x – 0) → y = mx + b

Esta expresión se conoce como la ecuación de la recta en la forma pendiente – intersección, ya que la recta queda determinada inequívocamente cuando se conoce su pendiente y su intersección con el eje vertical.

Conocer solamente la pendiente no es suficiente para caracterizar una recta sobre el plano, ya que infinitas rectas podrían tener la misma pendiente, lo cual significa que son paralelas, pero pasar por otros puntos.

Ejercicios resueltos

– Ejercicio 1

Encontrar la pendiente de la recta que se muestra en la siguiente figura:

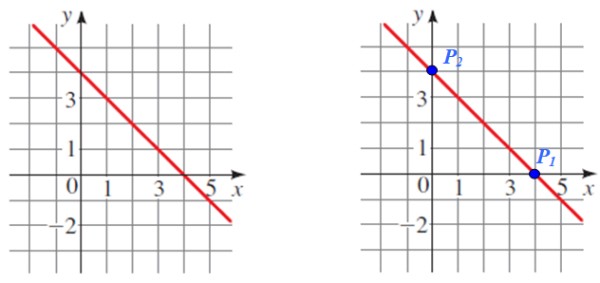
Solución

P₁ y P₂ son dos puntos de fácil lectura que servirán para el cálculo, nótese también que son las respectivas intersecciones con los ejes coordenados.

Las coordenadas de cada punto son:

P₁ (4,0) y P₂ (0,4)

Al sustituir en la ecuación para la pendiente:

m = (4 – 0) / (0 – 4) = 4 / (- 4) = -1

La pendiente es negativa, lo cual era de esperar luego de observar la gráfica.

– Ejercicio 2

Encontrar la ecuación de la recta que pasa por el punto (1, -6) y es paralela a la recta y = 2x – 3.

Solución

La pendiente de la recta buscada tiene que ser la misma que la de y = 2x – 3, pues son paralelas. Para esta recta la pendiente es m = 2, por lo tanto la que buscamos tiene la forma:

y – y₁ = 2 (x – x₁)

Ahora sustituimos el punto por el que pasa nuestra recta: x₁ = 1 y y₁ = -6.

y – (-6)= 2 (x – 1)

Por lo tanto y = 2x – 2 – 6 → y = 2x – 8

Ejemplos

Dos cantidades se pueden relacionar de tal manera que su gráfica sea una línea recta. En ese caso se dice que las cantidades tienen dependencia lineal y la pendiente de la recta se puede interpretar como la razón de cambio de una variable a la otra.

Ejemplo 1

Supongamos una piscina se llena de agua a una tasa constante en el tiempo. Como es natural, cuanto más tiempo pasa, más agua se almacena. Pues bien, la tasa a la que se llena la piscina es justamente la pendiente de la recta que relaciona el volumen con el tiempo:

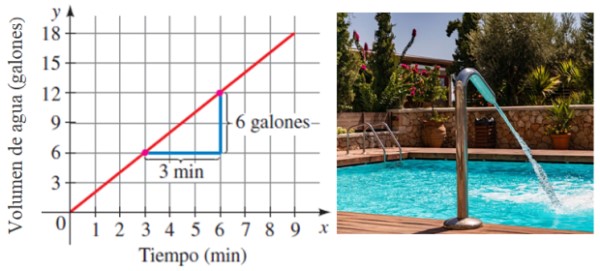
En este ejemplo, la piscina se llena a razón de 6/3 galones por minuto o 2 galones/minuto.

Ejemplo 2

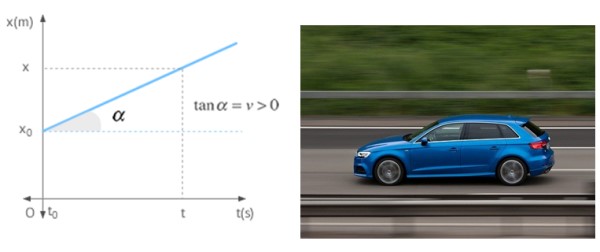
Cuando un móvil se desplaza en línea recta con velocidad constante, la pendiente de la gráfica posición en función del tiempo no es otra que dicha velocidad. En la gráfica se muestra un móvil con velocidad positiva, lo que significa que se está alejando del origen.

Referencias

1. Alvarez, J. La pendiente de una carretera. Recuperado de: geogebra.es.
2. Carena, M. 2019. Manual de Matemática Preuniversitaria. Universidad Nacional del Litoral.
3. Hoffman, J. Selección de temas de Matemática. Volumen 4.
4. Jiménez, R. 2008. Álgebra. Prentice Hall.
5. Stewart, J. 2006. Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.
6. Zill, D. 1984. Álgebra y Trigonometría. McGraw Hill.