Matemáticas

Factor común: características, ejemplos, ejercicios

El factor común de una expresión algebraica es una cantidad que está presente en todos los términos de esta. Cuando se conoce el factor común, es posible escribir la expresión de una manera equivalente mediante un producto de factores.

No todas las expresiones algebraicas poseen un factor común, las hay que solamente pueden dividirse entre ellas mismas y el 1, por lo tanto no es posible escribirlas como producto de factores. Un ejemplo de expresión que no tiene factor común es:

x + y

En cambio esta sí:

5a + 10b

Se ve que el 5 se encuentra presente en ambos términos, ya que 10 = 5∙2. Puesto que 5 es el factor común, entonces se puede escribir lo siguiente:

5a + 10b = 5∙(a + 2b)

El lector puede comprobar mediante la propiedad distributiva, que la expresión de la derecha es igual a la original.

El factor común también puede ser literal o una combinación de números y letras, por ejemplo en 4x2 − 2x. La x y el 2 se encuentran entre los factores y la expresión queda como producto:

4x2 − 2x = 2x⋅(x−1)

La ventaja de hallar el factor común de una expresión y escribirla como producto es que casi siempre se hace más fácil operar con ella. Por eso se utiliza en muchos procedimientos algebraicos y de cálculo como:

-Al resolver ecuaciones, cuyas soluciones se ponen de manifiesto rápidamente cuando se encuentra el factor común.

-Al calcular un límite con una indeterminación, esta puede desaparecer factorizando apropiadamente.

-La factorización adecuada también facilita las operaciones con expresiones algebraicas racionales, tales como sumas y restas.

Índice del artículo

Características del factor común

Las principales características del factor común son las siguientes:

-Puede ser un número, una expresión algebraica, o una combinación de ambos.

-El factor común debe estar contenido en cada uno de los términos de la expresión a factorizar.

-Según la cantidad de términos que contenga,  puede darse el caso de:

  1. Factor común monomio, si el factor común es de un solo término,
  2. Factor común binomio si tiene dos términos y
  3. Factor común polinomio, si el factor común consta de varios términos.

¿Cómo hallar el factor común de una expresión algebraica?

Para encontrar el factor común presente en un polinomio, hay que calcular el máximo común divisor o MCD de los coeficientes numéricos de todos los términos, así como de las letras o literales de cada término y escoger la potencia con el menor exponente.

Las letras o literales pueden presentarse como monomios, binomios o polinomios, tal como se verá en los ejemplos siguientes.

Lo más recomendable para comprender el proceso de obtener el factor común, es seguir los ejemplos y practicar resolviendo varios ejercicios de cada caso.

Ejemplos de factor común

No hay que perder de vista que la meta de la factorización por factor común es convertir una expresión en un producto indicado de factores. Seguidamente se analizan los casos más relevantes:

Factor común monomio

Se tienen los siguientes monomios (expresiones algebraicas de un solo término):

2x2;  10x4y;  100x6y2

¿Cuál puede ser el factor común a los tres?

Comenzando por los coeficientes numéricos: 2, 10 y 100, todos son pares y su MCD es 2. En cuanto a la parte literal, la variable x está presente en los tres términos, y la menor potencia es x2, luego el factor común es 2x2.

Los tres términos propuestos se pueden escribir como productos de dicho factor de esta forma:

2x2= 2x2∙1

10x4y = 2x2 ∙ 5x2y

100x6y2= 2x2∙ 50x4y2

Multiplicando los factores de la derecha, se puede verificar que se obtiene el término de la izquierda.

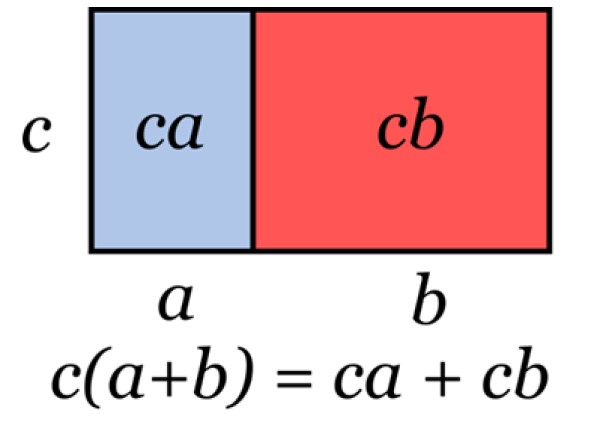
Esta técnica se aplica cuando se necesita factorizar una expresión algebraica, como en los ejemplos que siguen:

  • Ejemplo 1

Factorizar la siguiente expresión:

5x3y + 10x2y2 + 5xy2

El MCD de los coeficientes numéricos de cada término es:

MCD (5,10) = 5

En cuanto a la parte literal, tanto la x como la y están presentes en los tres términos y el menor exponente de cada una es 1, por lo tanto el factor común es 5xy y se puede escribir:

5x3y + 10x2y2 + 5xy2= 5xy∙(x2 +2xy2+y)

Factor común polinomio

El factor común puede consistir en un binomio, un trinomio o en general en un polinomio. En tal caso siguen siendo válidas las instrucciones del apartado anterior, escogiendo como  factor común el que tenga el menor exponente.

  • Ejemplo 2

Escribir la siguiente expresión como el producto de dos factores:

2a(x−1) – 3b(x−1)

Por inspección directa, el factor común es el binomio (x–1), entonces:

2a(x−1) – 3b(x−1)= (x-1)∙(2a – 3b)

Factorización por agrupación de términos

En ocasiones la existencia de un factor común no es evidente, pero se pone de manifiesto si los términos se agrupan de una manera conveniente:

  • Ejemplo 3

Factorizar 3x3 – 9ax2 – x + 3a

A primera vista no hay factor común en estos cuatro términos, ya que por ejemplo la x está presente en los tres primeros, pero no en el último. Y la a se encuentra en el segundo y en el último nada más.

En cuanto a los coeficientes, hay tres términos en los que el 3 está presente, sin embargo para ser factor común debería estar en todos los términos.

Pareciera que las técnicas descritas no se pueden aplicar en esta oportunidad. No obstante, la expresión se puede factorizar agrupando los dos primeros términos y los dos últimos, teniendo cuidado al colocar los paréntesis, de que los signos sean los apropiados para no alterar la original:

3x3 – 9ax2 – x + 3a = (3x3 – 9ax2) – (x – 3a)

Nótese el signo negativo en medio de los paréntesis: es necesario, porque de lo contrario la expresión original cambiaría.

En el paréntesis izquierdo el factor común es 3x2, por lo tanto:

(3x3 – 9ax2) – (x – 3a) = 3x2⋅ (x – 3a) – (x – 3a)

Y se observa que ya apareció un factor común: (x – 3a), es decir, que se factoriza por segunda vez para obtener:

3x2 (x– 3a) – (x – 3a) = (x – 3a)∙(3x2– 1)

Ejercicios de factor común

Ejercicio 1

Resolver la ecuación 4x3 +7x2  +6x = 0

Solución

La “x” es factor común, por lo tanto:

3x3 −5x2  +2x =   x(3x2 −5x  +2) = 0

Para que la expresión a la izquierda sea 0, basta con que se cumpla alguna de estas dos condiciones:

x = 0

O:

3x2 −5x  +2 =0

Esta es una ecuación de segundo grado completa que se puede resolver aplicando la fórmula general, también mediante el uso de una calculadora científica u otro método algebraico. Las soluciones de esta ecuación son:

x = 1

x=2/3

Una vez halladas, es ilustrativo escribir la ecuación como el producto de 3 factores, aunque el enunciado no lo pidió. Quedaría así:

x⋅(x-1)⋅(x-2/3) = 0

Ejercicio 2

Calcular el siguiente límite si es que existe:

Solución

Primero se sustituye en x = −2 para intentar evaluar el límite, al hacerlo se obtiene:

Como se trata de una indeterminación de la forma 0/0, hay que factorizar para intentar eliminarla. El denominador no se puede factorizar, pero el numerador sí.

En el numerador el factor común es x:

x2+2x = x∙ (x+2)

Se sustituye la expresión factorizada en el límite y de esta manera la indeterminación desaparece:

Se concluye que el límite existe y vale −2.

Referencias

  1. Baldor, A. 2005. Álgebra. Grupo Patria Cultural.
  2. Jiménez, R. 2008. Álgebra. Prentice Hall.
  3. Larson, R. 2012. Precálculo. 8va. Edición. Cengage Learning.
  4. Stewart, J. 2007. Precálculo: Matemáticas para el cálculo. 5ta. Edición. Cengage Learning.
  5. Zill, D. 1984. Álgebra y Trigonometría. McGraw Hill.