Energía libre de Gibbs: unidades, cómo se calcula, ejercicios resueltos
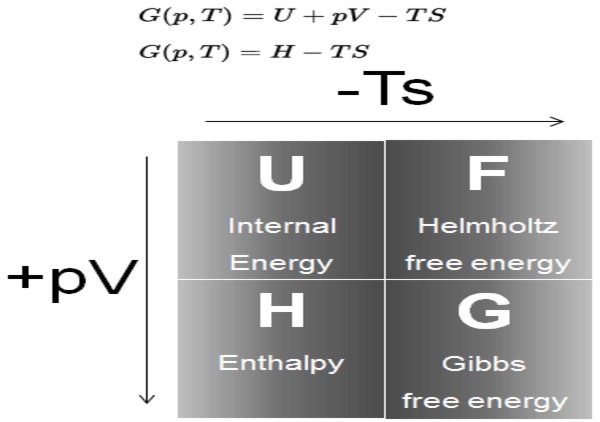
La energía libre de Gibbs (comúnmente denominada G) es un potencial termodinámico definido como la diferencia de la entalpía H, menos el producto de la temperatura T, por la entropía S del sistema:
G = H – T S
La energía libre de Gibbs se mide en Joules (de acuerdo al Sistema Internacional), en ergios (para el Sistema Cegesimal de Unidades), en calorías o en electrón voltios (para electro Voltios).
En los procesos que ocurren a presión y temperatura constante, la variación de la energía libre de Gibbs es ΔG = ΔH – T ΔS. En tales procesos, (G) representa la energía disponible en el sistema que puede convertirse en trabajo.
Por ejemplo, en las reacciones químicas exotérmicas, la entalpía disminuye mientras la entropía aumenta. En la función de Gibbs estos dos factores se contrarrestan, pero solo cuando la energía de Gibbs decrece la reacción se produce espontáneamente.
Entonces, si la variación de G es negativa, el proceso es espontáneo. Cuando la función de Gibbs alcanza su mínimo, el sistema alcanza un estado de equilibrio estable. En síntesis, en un proceso para el que la presión y la temperatura se permanecen constantes podemos afirmar:
– Si el proceso es espontáneo, entonces ΔG 0
– Cuando el sistema está en equilibrio: ΔG = 0
– En un proceso no-espontáneo G aumenta: ΔG > 0.
Índice del artículo
La energía libre de Gibbs (G) se calcula mediante la definición dada al comienzo:
G = H – T⋅S
A su vez, la entalpía H es un potencial termodinámico definido como:
H = U + P V
A continuación se hará un análisis paso a paso, para conocer las variables independientes de las cuales la energía de Gibbs es una función:
1- De la primera ley de la termodinámica se tiene que la energía interna U se relaciona con la entropía S del sistema y su volumen V para procesos reversibles mediante la relación diferencial:
dU = dQ – dW = TdS – PdV
De esta ecuación se deduce que la energía interna U es una función de las variables S y V:
U = U(S,V)
2- Partiendo de la definición de H y tomando el diferencial se obtiene:
dH = dU + d(P V) = dU + VdP + PdV
3- Sustituyendo la expresión para dU obtenida en (1) se tiene que:
dH = TdS – PdV + VdP + PdV = TdS + VdP
De aquí se concluye que la entalpía H depende de la entropía S y de la presión P, es decir:
H = H(S,P)
4- Ahora se calcula el diferencial total de la energía libre de Gibbs obteniéndose:
dG = dH -TdS -SdT = TdS + VdP -TdS -SdT
Donde se ha sustituido dH por la expresión hallada en (3).
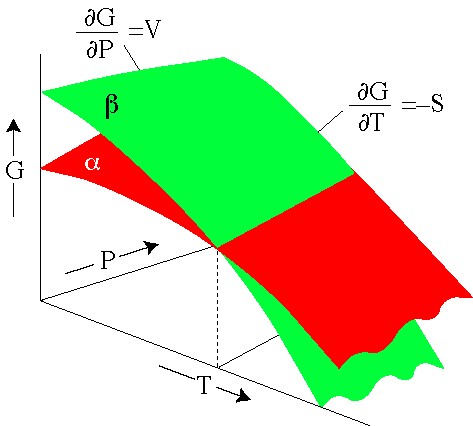
5- Finalmente, al simplificar se obtiene: dG = VdP – SdT, quedando claro que la energía libre G depende de la presión y la temperatura T como:
G = G(P, T)
Del análisis en el apartado anterior se deduce que la energía interna de un sistema es función de la entropía y el volumen:
U = U(S, V)
Entonces el diferencial de U será:
dU = ∂SU|V dS + ∂VU|S dV = TdS – PdV
De esta expresión en derivadas parciales, se pueden deducir las llamadas relaciones termodinámicas de Maxwell. Las derivadas parciales se aplican cuando una función depende de más de una variable y se calculan fácilmente aplicando el teorema de la siguiente sección.
Primera relación de Maxwell
∂VT|S = -∂SP|V
Para llegar a esta relación se ha usado el teorema de Clairaut – Schwarz sobre las derivadas parciales, que afirma lo siguiente:
“Las derivadas mixtas de segundo orden con las variables intercambiadas son iguales, siempre que las funciones a ser derivadas sean continuas y diferenciables”.
Segunda relación de Maxwell
Partiendo de lo demostrado en el punto 3 de la sección previa:
H = H(S, P) y dH=TdS + VdP
Puede obtenerse:
∂PT|S = ∂SV|P
Se procede en forma similar con la energía libre de Gibbs G = G(P, T) y con la energía libre de Helmholtz F = F(T, V) para obtener las otras dos relaciones termodinámicas de Maxwell.

Las cuatro relaciones termodinámicas de Maxwell
1- Asociada a la energía interna U: ∂VT|S = -∂SP|V
2- La que se obtiene a partir de la entalpía H: ∂PT|S = ∂SV|P
3- Relacionada con la energía de Helmholtz F: ∂TP|V = ∂VS|T
4- Vinculada a la energía libre de Gibbs G: ∂TV|P = -∂PS|T
Calcular la variación de la energía libre de Gibbs para 2 moles de gas ideal a temperatura de 300K durante una expansión isotérmica que lleva al sistema de un volumen inicial de 20 litros hasta un volumen final de 40 litros.
Solución
Recordando la definición de la energía libre de Gibbs se tiene:
G = H – T S
Entonces una variación finita de F será:
ΔG = ΔH – T ΔS, ya que ΔT = 0
En los gases ideales la entalpía solo depende de la temperatura absoluta del mismo, pero como se trata de un proceso isotérmico, entonces ΔH = 0 y ΔG = – T ΔS.
Para los gases ideales la variación de entropía de un proceso isotérmico es:
ΔS = nR ln(V2/V1)
Que aplicado al caso de este ejercicio nos queda:
ΔS = 2 moles x 8,314 J/(K mol) x ln(40L/ 20L) = 11,53 J/K
Luego podemos obtener el cambio en la energía de Helmholtz:
ΔG = – 300K x 11,53 J/K = -3457,70 J.
Tomando en cuenta que la energía libre de Gibbs es una función de la temperatura y la presión G = G(T,P); determinar la variación de G durante un proceso en el que la temperatura no cambia (isotérmico) para n moles de un gas ideal monoatómico.
Solución
Tal como se demostró más arriba, el cambio de la energía de Gibbs solo depende del cambio en la temperatura T y del volumen V, por lo que una variación infinitesimal del mismo se calcula de acuerdo a:
dG = -SdT + VdP
Pero si se trata de un proceso en el que la temperatura es constante entonces dF = + VdP, por lo que una variación finita de presión ΔP conduce a un cambio en la energía de Gibbs dada por:
ΔG = + ∫ VdP = + ∫(n R T) dP/P = + n R T ln(ΔP)
Usando la ecuación del gas ideal:
P V = n R T
Durante un proceso isotérmico ocurre que:
d(P V) = P dV + V dP = 0
Es decir que:
dP/P = – dV/V
Por lo que el resultado anterior puede escribirse en función de la variación del volumen ΔV:
ΔG = + ∫ VdP = + ∫(n R T) dP/P = – ∫(n R T) dV/V = -n R T ln(ΔV)
Considerando la siguiente reacción química:
N20 (g) + (3/2) O2 (g) ↔️ 2NO2 (g) a temperatura T=298 K
Hallar la variación de la energía libre de Gibbs y mediante el resultado obtenido, indicar si se trata o no de un proceso espontáneo.
Solución
A continuación los pasos:
– Primer paso: las entalpías de reacción
ΔHr = 2*ΔH( NO2 (g)) – ΔH( N20 (g)) = 2*33,2-81,6 = -15,2kJ/mol
– Segundo paso: la variación de entropía de reacción
ΔSr = 2*S( NO2 (g)) – S( N20 (g)) – (3/2) S( O2 (g))= 2*240,1 – 220,1 – 1,5*205,2 = -47,7 J/(mol*K).
– Tercer paso: variación en la función de Gibbs
Este valor determinará el balance entre la energía decreciente y la entropía creciente para saber si finalmente la reacción es espontánea o no.
ΔGr = ΔHr – T ΔSr = -15,2 -298*(-47,7) = -985,4 J/mol
Como se trata de una variación negativa de la energía de Gibbs puede concluirse que se trata de una reacción espontánea a la temperatura de 298 K = 25 ºC.
- Castaños E. Ejercicios de energía libre. Recuperado de: lidiaconlaquimica.wordpress.com.
- Cengel, Y. 2012. Termodinámica. 7ma Edición. McGraw Hill.
- Libretexts. Gibbs Free Energy. Recuperado de: chem.libretexts.org
- Libretexts. What are Free Energies. Recuperado de: chem.libretexts.org
- Wikipedia. Energía de libre de Gibbs. Recuperado de: es.wikipedia.com
- Wikipedia. Gibbs free energy. Recuperado de: en.wikipedia.com
