Media ponderada: cómo se calcula, ejemplos y ejercicios
La media ponderada o media aritmética ponderada, es una medida de tendencia central en la cual, a cada valor xi que puede tomar una variable X, se le asigna un peso pi. Como resultado de ello, al denotar a la media ponderada por xp, se tiene:
Con la notación de sumatoria, la fórmula para la media ponderada es:
Donde N representa la cantidad de valores que se escogen de la variable X.
El pi, al que también se le llama factor de ponderación, es una medida de la importancia que el investigador le asigna a cada valor. Dicho factor es arbitrario y siempre positivo.
En esto que la media ponderada se diferencia de la media aritmética simple, porque en esta, cada uno de los valores xn tiene igual significancia. Sin embargo, en numerosas aplicaciones, el investigador posiblemente considere que algunos valores son más importantes que otros y les asignará un peso según su criterio.
Aquí está el ejemplo más conocido: supongamos que un estudiante presenta N evaluaciones en una materia y todas tienen el mismo peso en la nota final. En tal caso, para calcular la nota definitiva bastará con hacer un promedio simple, es decir, sumar todas las calificaciones y dividir el resultado entre N.
Pero si cada actividad tiene un peso diferente, porque algunas evalúan contenidos más importantes o más complejos, entonces será necesario multiplicar cada evaluación por su respectivo peso, y después sumar los resultados para obtener la calificación definitiva. Veremos cómo llevar a cabo este procedimiento en la sección de ejercicios resueltos.
Índice del artículo

El ejemplo de las calificaciones antes descrito es uno de los más típicos en cuanto a la aplicación de la media ponderada. Otra aplicación muy importante en economía es el índice de precios de consumo o índice de precios al consumidor IPC, también llamada canasta familiar y que sirve como evaluador de la inflación en una economía.
En su elaboración se toman en cuenta una serie de rubros como alimentos y bebidas no alcohólicas, ropa y calzado, medicinas, transporte, comunicaciones, educación, ocio y otros bienes y servicios.
Los expertos asignan a cada rubro un factor de ponderación, según su importancia en la vida de las personas. Los precios se recogen durante un período de tiempo establecido, y con toda la información se calcula el IPC de dicho período, que puede ser mensual, bimensual, semestral o anual, por ejemplo.
En física, la media ponderada tiene una importante aplicación, que es calcular el centro de masas de un sistema partículas. Este concepto es muy útil cuando se trabaja con un cuerpo extendido, en el cual se debe tomar en cuenta su geometría.
El centro de masas se define como el punto en el cual se concentra toda la masa de un objeto extendido. Sobre este punto se pueden aplicar las fuerzas como el peso, por ejemplo, y así explicar sus movimientos de traslación y rotación, mediante las mismas técnicas con las que se trabajaba cuando se suponía que todos los objetos eran partículas.
Por simplicidad, se comienza suponiendo que el cuerpo extendido está compuesto de una cantidad N de partículas, cada una de ellas con masa m y su propia ubicación en el espacio: el punto de coordenadas (xi, yi, zi).
Sea xCM la coordenada x del centro de masas CM, entonces:
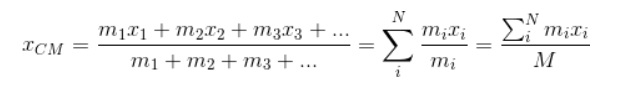
M representa la masa total del sistema. Se procede de la misma manera para encontrar las coordenadas yCM y zCM:
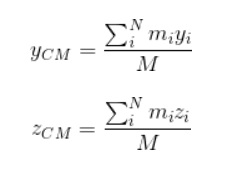
El factor de ponderación en este caso es la masa de cada una de las partículas que constituyen el objeto extendido.
Características importantes del centro de masas
Cuando el número de partículas es muy grande, se trata de un objeto continuo. En tal caso N → ∞ y la sumatoria se reemplaza por una integral definida, cuyos límites vienen dados por el tamaño del objeto.
Es importante destacar el hecho de que no necesariamente hay masa en la ubicación del centro de masas. Por ejemplo en una rosquilla o donut, el centro de masa coincide más o menos con el centro geométrico de la rosquilla.

La localización del centro de masas tampoco depende del sistema de referencia que se use para establecer las posiciones de las partículas, ya que es una propiedad que depende de la propia configuración del objeto y no de cómo se vea desde diversos marcos de referencia.
En muchos casos, los profesores asignan diferentes pesos o porcentajes a cada actividad de evaluación en su cátedra. Así por ejemplo, las tareas tienen un porcentaje, los exámenes cortos otro diferente y el examen de fin de curso uno probablemente mucho mayor.
Supóngase que en una cierta asignatura, las actividades de evaluación y sus ponderaciones respectivas son las siguientes:
-Tareas para la casa: 20 %
-Exámenes cortos: 25 %
-Informes de Laboratorio: 25 %
-Examen final: 30 %
a) ¿De qué manera calcula el profesor la nota final de esta asignatura para cada estudiante?
b) Suponga que las calificaciones de un alumno en particular son, en la escala del 1 al 5, las siguientes:
-Tareas: 5.0 puntos
-Exámenes cortos: 4.7 puntos
-Informes de Laboratorio: 4.2 puntos
-Examen final: 3.5 puntos
Encontrar la nota definitiva del estudiante en esta asignatura.
Solución
a) Cada evaluación tiene un peso distinto, que el profesor ha asignado de acuerdo a la complejidad de las mismas y a su propio criterio. De esta forma, la calificación definitiva se calcula directamente como:
Definitiva = (Tareas x20 % + Exámenes Cortos x25 % + Informes x25 % + Examen final x30 %) / 100
b) Definitiva = (5.0 x 0.2) + (4.7 x 0.25) + (4.2 x 0.25) + (3.5 x 0.3) puntos =4.275 puntos ≈ 4.3 puntos
Los dueños de una tienda de ropa compraron pantalones vaqueros a tres diferentes proveedores.
El primero les vendió 12 unidades a un precio de 15 € cada una, el segundo 20 unidades a 12.80 € cada una y a un tercero le compraron un lote de 80 unidades a 11.50 €.
¿Cuál es el precio promedio que han pagado los dueños de la tienda por cada vaquero?
Solución
xp = (12 x 15 + 20 x 12.80 +80 x 11.50) / (12+20+80) € = 12.11 €
El valor de cada vaquero es 12.11 €, sin importar que algunos costaran un poco más y otros un poco menos. Habría sido exactamente igual si los dueños de la tienda hubieran comprado los 112 vaqueros a un proveedor único que se los hubiera vendido en 12.11 € la pieza.
- Arvelo, A. Medidas de Tendencia Central. Recuperado de: franarvelo.wordpress.com
- Mendenhall, W. 1981. Estadística para Administración y Economía. 3ra. edición. Grupo Editorial Iberoamérica.
- Moore, D. 2005. Estadística Básica Aplicada. 2da. Edición.
- Triola, M. 2012. Elementary Statistics. 11th. Ed. Pearson Education.
- Wikipedia. Media ponderada. Recuperado de: en.wikipedia.org
