Teorema de Steiner: explicación, aplicaciones, ejercicios
El teorema de Steiner, también conocido como teorema de los ejes paralelos, permite evaluar el momento de inercia de un cuerpo extendido, alrededor de un eje que sea paralelo a otro que pase por el centro de masa del objeto.
Fue descubierto por el matemático suizo Jakob Steiner (1796 –1863) y afirma lo siguiente: sea ICM el momento de inercia del objeto respecto a un eje que pasa por su centro de masas CM e Iz el momento de inercia respecto a otro eje paralelo a este.

Conocida la distancia D que separa a ambos ejes y la masa M del cuerpo en cuestión, el momento de inercia respecto al eje incógnito es:
Iz = ICM + MD2
El momento de inercia indica cuan fácil es para un objeto de rotar alrededor de cierto eje. Depende no solamente de la masa del cuerpo, sino de cómo esta se distribuye. Por este motivo se lo conoce también como inercia rotacional, siendo sus unidades en el Sistema Internacional Kg . m2.
El teorema muestra que el momento de inercia Iz siempre es mayor que el momento de inercia ICM en una cantidad dada por M.D2.
Índice del artículo
Como un objeto es capaz de rotar alrededor de numerosos ejes, y en las tablas por lo general se da solamente el momento de inercia respecto al eje que pasa por el centroide, el teorema de Steiner facilita el cálculo cuando se necesita hacer girar cuerpos sobre ejes que no coinciden con este.
Por ejemplo, una puerta comúnmente no gira alrededor de un eje que pase por su centro de masas, sino respecto a un eje lateral, donde se adhieren las bisagras.
Al conocer el momento de inercia es posible calcular la energía cinética asociada a la rotación sobre dicho eje. Si K es la energía cinética, I el momento de inercia alrededor del eje en cuestión y ω la velocidad angular, se cumple que:
K = ½ I.ω2
Esta ecuación se parece mucho a la muy familiar fórmula de la energía cinética para un objeto de masa M moviéndose a velocidad v: K =½ M.v2. Y es que el momento de inercia o inercia rotacional I desempeña en la rotación el mismo rol que la masa M en la traslación.
El momento de inercia de un objeto extendido se define como:
I=∫r2 dm
Donde dm es una porción infinitesimal de masa y r es la distancia entre dm y el eje de rotación z. En la figura 2 este eje atraviesa al centro de masa CM, sin embargo puede ser cualquiera.
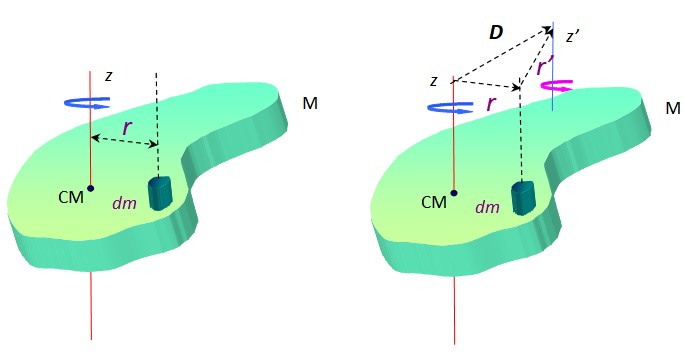
Alrededor de otro eje z’, el momento de inercia es:
Iz=∫(r’)2 dm
Ahora bien, de acuerdo el triángulo formado por los vectores D, r y r’ (ver figura 2 a la derecha), hay una suma vectorial:
r + r’ = D → r’ = D – r
Los tres vectores se encuentran sobre el plano del objeto que puede ser el xy. El origen del sistema coordenadas (0,0) se escoge en CM para facilitar los cálculos que siguen.
De esta forma el módulo al cuadrado del vector r’ es:
(r’)2 = (Dx– rx)2 +(Dy – ry)2 =
= Dx2 + Dy2 +rx2 + ry2 -2Dxrx – 2 Dyry =
= D2 + r2 – 2Dxrx – 2 Dyry
Ahora se sustituye este desarrollo en la integral del momento de inercia Iz y además se usa la definición de densidad dm = ρ.dV:
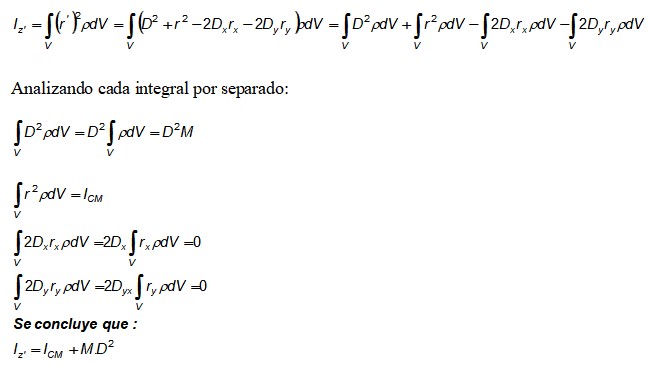
El término M. D2 que aparece en el teorema de Steiner proviene de la primera integral, la segunda es el momento de inercia respecto al eje que pasa por CM.
Por su parte, la tercera y la cuarta integrales valen 0, puesto que por definición constituyen la posición del CM, la cual se ha elegido como el origen del sistema de coordenadas (0,0).
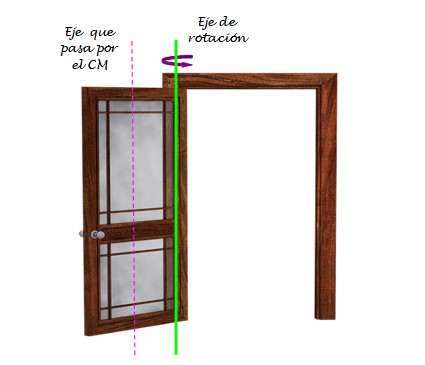
La puerta rectangular de la figura 1 tiene una masa de 23 Kg, 1,30 de ancho y 2,10 m de alto. Determinar el momento de inercia de la puerta respecto al eje que pasa por los goznes, suponiendo que la puerta es delgada y uniforme.
Solución
A partir de una tabla de momentos de inercia, para una placa rectangular de masa M y dimensiones a y b, el momento de inercia respecto al eje que pasa por su centro de masa es: ICM = (1/ 12)M(a2 + b2).
Se supondrá una puerta homogénea (una aproximación, puesto que la puerta de la figura probablemente no lo sea tanto). En tal caso, el centro de masa pasa por su centro geométrico. En la figura 3 se ha dibujado un eje que pasa por el centro de masas y que además es paralelo al eje que pasa por los goznes.
ICM = (1/12) x 23 Kg x (1.302+2.102) m2 = 11.7 Kg.m2
Aplicando el teorema de Steiner para el eje de rotación verde:
I = ICM + MD2 = 11.7 Kg.m2 + 23 Kg x 0.652 m2 = 21.4 Kg.
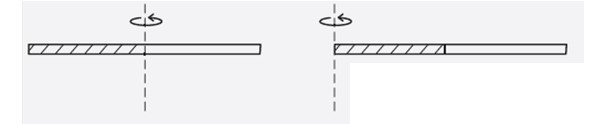
Encuentre el momento de inercia de una varilla delgada homogénea cuando gira respecto a un eje que pasa por uno de sus extremos, ver figura. ¿Es mayor o menor que el momento de inercia cuando gira alrededor de su centro? ¿Por qué?
Solución
Según la tabla de momentos de inercia, el momento de inercia ICM de una varilla delgada de masa M y longitud L es: ICM = (1/12)ML2
Y el teorema de Steiner afirma que cuando se la hace girar alrededor de un eje que pasa por un extremo D = L/2 queda:
I = ICM + MD2 = (1/12)ML2 + M (L/2)2=(1/3)ML2
Es mayor, aunque no simplemente el doble, sino 4 veces más, ya que la otra mitad de la varilla (sin sombrear en la figura) gira describiendo un radio más grande.
La influencia de la distancia al eje de giro no es lineal, sino cuadrática. Una masa que esté al doble de la distancia que otra, tendrá un momento de inercia proporcional a (2D)2 = 4D2.
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill. 313-340.
- Georgia State University. Rotational Motion. Recuperado de: phys.nthu.edu.tw.
- Parallel Axis Theorem. Recuperado de: hyperphysics.phy-astr.gsu.edu.
- Rex, A. 2011. Fundamentos de Física. Pearson. 190-200.
- Wikipedia. Parallel axis theorem. Recuperado de: en.wikipedia.org
