Interpolación lineal: fórmulas, cómo hacerla, ejemplos, ejercicios

¿Qué es la interpolación lineal?

La interpolación lineal consiste en estimar la ubicación de un punto dentro de un intervalo numérico, suponiendo que los valores extremos de dicho intervalo están unidos por una recta. Conocida la ecuación de esta recta, es posible ubicar el punto desconocido.

La idea se esquematiza en la siguiente figura, en la cual se muestra un acercamiento a la gráfica de una función entre los puntos A y B. Suponiendo que estos puntos están cercanos, es posible aproximar la curva que los une mediante una recta y encontrar así los puntos intermedios.

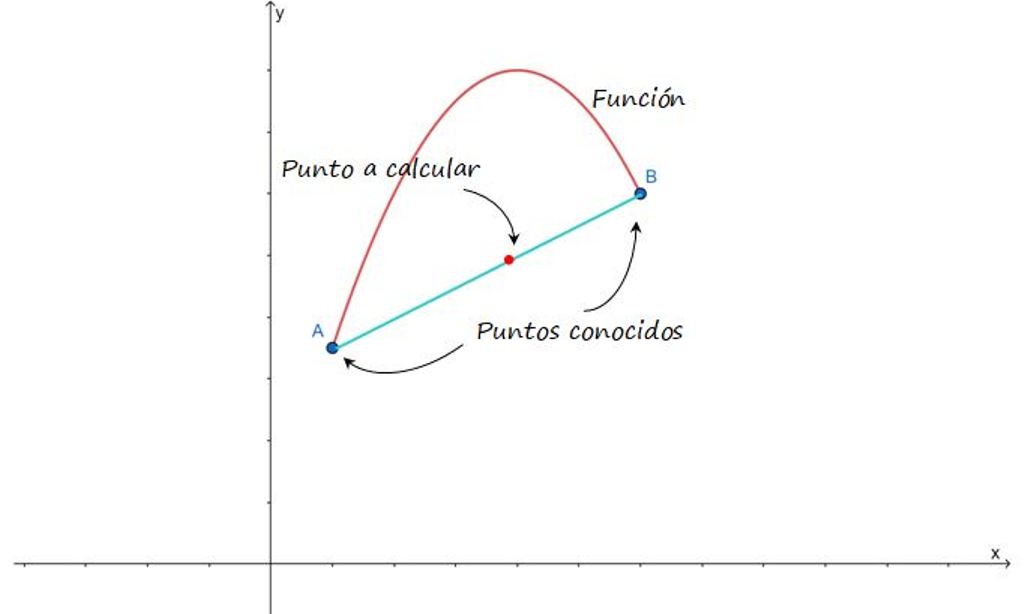
También se puede aproximar la curva que une a los puntos dados mediante una función cuadrática u otro polinomio. Sin embargo la recta tiene la ventaja de su sencillez matemática, por lo cual resulta fácil de manejar, aunque siendo la interpolación más simple de todas, es posible que el resultado no sea tan preciso como el que se obtiene al emplear otras funciones.

Fórmulas

Se tienen dos puntos de coordenadas [x_o, f(x_o)] y [x₁, f(x₁)] entre los cuales está el punto [x, g(x)], cuyas coordenadas se desea conocer.

El primer paso consiste en unir los puntos conocidos mediante un segmento de recta, sobre el cual se encuentran las coordenadas del punto a calcular.

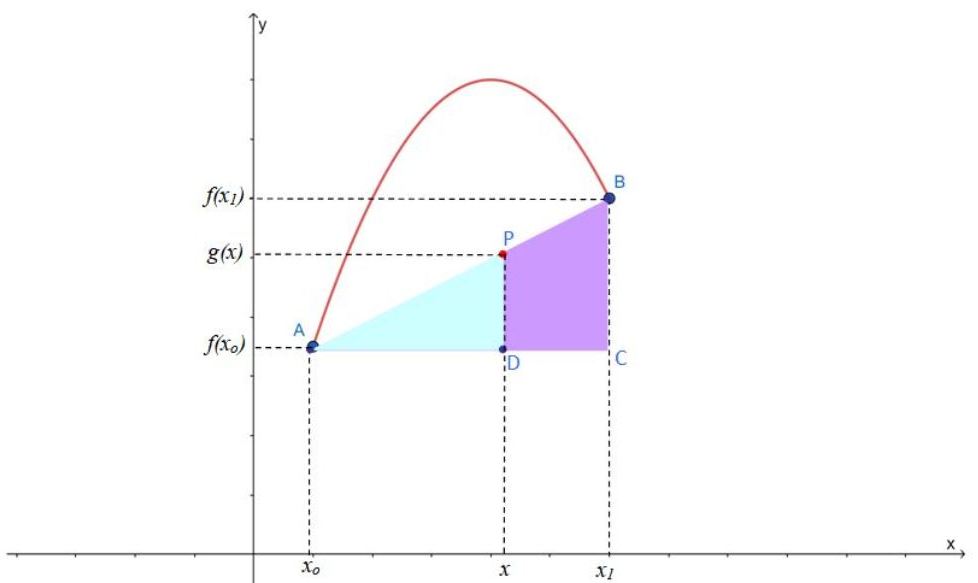
Como se puede ver, se forman dos triángulos rectángulos: ABC y APD, que además tienen un ángulo agudo en común, por lo que son triángulos semejantes, a los que se puede aplicar el teorema de Thales:

f₁(x₁) = y₁ ; f_o(x_o) = y_o ; g(x) = y

La ecuación de arriba se transforma en:

Margen de error

Cuando se aproxima una función con este método, la cota de error viene dada por el valor absoluto de la diferencia entre la función f(x) y la recta interpoladora g(x):

Error = │f(x) − g(x) │

¿Cómo hacer una interpolación lineal?

Llevar a cabo una interpolación lineal es muy simple, solo hay que seguir estos pasos:

Paso 1

Determinar el punto incógnita P(x,y).

Paso 2

Establecer los dos puntos que limitan el intervalo donde se encuentra el valor a calcular, es decir, los puntos (x_o,y_o) y (x₁, y₁).

Paso 3

Sustituir todos los valores en la ecuación:

Y calcular el resultado.

Ejemplos de interpolación lineal

Ejemplo 1

Se quiere hallar el valor aproximado de ln 3 a través de una interpolación lineal, dados los siguientes valores:

ln 2 = 0.693147 y ln 4 = 1.386294

Comparar el resultado con el valor de ln 3 obtenido a través de una calculadora y determinar el margen error cometido.

• Paso 1

Para encontrar el valor aproximado de ln 3 hay que proceder siguiente modo: en primer lugar se establece la incógnita, que es y = ln 3, junto a su correspondiente valor de “x”: x = 3. Este es el punto que se quiere calcular: (3, ln 3).

• Paso 2

Después hay que establecer los puntos límites del intervalo con los valores conocidos. Se pide hacerlo con la siguiente pareja de puntos:

• Límite inferior: [x_o = 2; y_o = ln 2 = 0.693147]
• Límite superior: [x₁ = 4; y₁ = ln 4 = 1.386294]

• Paso 3

Los valores determinados en los pasos 1 y 2 se sustituyen cuidadosamente en la ecuación para generar el resultado de la aproximación a ln 3:

ln 3 =1.098612

Y el margen de error es:

Error = │1.098612 − 1.03971 │= 0.059

El error porcentual de la interpolación se calcula dividiendo el error entre el valor real de ln3 y multiplicando por 100 %:

Error porcentual = (Error/Valor real)× 100 = (0.059/1.098612)×100% = 5.4%

Ejemplo 2

Ahora se desea hallar el valor aproximado de ln 3 mediante interpolación lineal, conocidos estos dos valores:

ln 2.5 = 0.916291 y ln 3.5 = 1.252763

Determinar también el error correspondiente y comparar con los resultados del ejemplo anterior.

• Paso 1

De nuevo el punto incógnita es:

y = ln 3, x = 3

• Paso 2

• Límite inferior: [x_o = 2.5; y_o = y_o = ln 2.5 = 0.916291]
• Límite superior: [x₁ = 3.5; y₁ = ln 3.5 = 1.252763]

• Paso 3

ln 3 =1.098612

Se determina la cota de error en este caso, que resulta:

Error = │1.098612 − 1.084527 │= 0.014

El error porcentual en este caso es ≈ 1.3 %. Comparando con la cota de error del ejemplo 1, el nuevo valor es más preciso, pues el intervalo elegido para interpolar es menor.

Ejercicios resueltos

Ejercicio 1

Calcular, mediante interpolación lineal, el calor específico del aire a presión constante c_p  y temperatura de 530 K, partiendo de la tabla de valores que se muestra a continuación.

• Solución

En la resolución de muchos problemas es frecuente que el valor que se busca no aparezca exactamente como se desea en la tabla de valores que se tiene a mano. Una alternativa es elegir el valor más cercano al deseado, pero muchas veces basta una interpolación lineal para encontrar una aproximación mucho mejor.

El valor de c_p a 530 K no aparece en la tabla adjunta, pero se puede hacer una interpolación lineal con los respectivos calores específicos a 500 K y 550 K, que son las temperaturas más cercanas a 530 K y cuyos calores específicos sí aparecen en la tabla mostrada.

Los respectivos calores específicos a presión constante para dichas temperaturas son:

T_o = 500 K; c_po = 1.029 kJ /kg∙K

T₁ = 550 K; c_p1 = 1.040 kJ /kg∙K

Y la incógnita es el punto (500K, c_p)

Sustituyendo en la fórmula de la interpolación lineal dada anteriormente, con T en el lugar de la variable “x” y c_p en lugar de “y”, se tiene:

Ejercicio 2

La carga aplicada a un resorte (en kilopondios) produce las siguientes elongaciones (en milímetros) de acuerdo a la tabla que se muestra:

Calcular la elongación cuando la carga es 12.6 kp.

• Solución

Sea y el valor de la elongación buscada cuando la carga es C = 12.6 kp. El punto incógnita es (12.6, y), que se encuentra entre los puntos:

C_o = 10 kp; y_o = 105 mm

C₁ = 15 kp; y₁ = 172 mm

Solo resta sustituir los valores en la ecuación:

Calcular el calor específico del aire a volumen constante para una temperatura de 727 K, utilizando interpolación lineal y la tabla de valores del ejercicio resuelto 1.

Referencias

1. Academia Rafa Vilchez. Cómo realizar una interpolación lineal. Recuperado de: academiarafavilchez.com
2. Chapra, S. 2007. Métodos Numéricos para Ingenieros. 5ta. Edición. McGraw Hill.
3. Khan Academy. Mathematics of linear interpolation. Recuperado de: khanacademy.org.
4. The Education Life. Linear Interpolation Formula. Recuperado de: theeducationlife.com
5. X-Engineer. Linear interpolation and extrapolation with calculator. Recuperado de: x-engineer.org.